The maximum aerobic power is an important predictor of endurance performance and is closely associated with an individual's Cardiorespiratory Fitness (CRF). Being able to screen for changes in CRF cost effectively as well as identifying variables to provide accurate values for aerobic fitness has been identified by numerous studies. The purpose of the present study was to investigate whether published models were valid predictors of CRF in young adults using previously unpublished 20 m SRT (shuttle run test) data.
Estimated values from 20m SRT performance were compared across three published models using an independent data set of 178 participants (89 men; age 22.8 ± 4.2 years, height 1.80 ± 0.07 m, body mass 79.8 ± 12.4 kg and 89 women; age 21.3 ± 2.4 years, height 1.67 ± 0.06 m, body mass 62.6 ± 9.3 kg). Closeness-of-fit was assessed using means and standard deviation and bias.
An allometric model provided a superior fit, with less bias, compared with two published linear regression equations. Directly measured values were 51.2 ± 8.6 ml kg-1 min-1 compared with 49.8 ± 9.3 (allometric model) versus 46.8 ± 7.9 and 44.4 ± 9.1 ml kg-1 min-1 for the two linear models respectively.
An allometric model provided more accurate predictions of CRF (ml kg-1 min-1) in young adults compared with two published linear models.
Allometry, 20-m shuttle run, Prediction, Aerobic fitness, Cardiorespiratory fitness, Young adults
• Directly measured Cardiorespiratory Fitness (CRF) is widely acknowledged as the 'Gold Standard' of aerobic fitness and is a key index of health as well as a valuable indicator of potential endurance performance. The 20 metre shuttle run test (20m SRT) is probably the best known and most widely used field test of CRF.
• The 20m SRT should be used as an indirect measure of CRF across the lifespan for screening and monitoring purposes. In order to provide accurate values of CRF in young adults practitioners should use values (ml kg-1 min-1) provided by an allometric model proposed by [1] rather than those values derived from linear regression models.
The maximum aerobic power is an important determinant of Cardiorespiratory Fitness (CRF), which is also identified as an individual's 'aerobic fitness'. CRF is an important determinant of athletic ability [2] as well as an index of overall health in youth [3] and adult [4] populations. Importantly high levels of CRF tend to ameliorate the effect of excess body fatness on cardiovascular risk factors in men and women [5]. The direct determination of the maximum oxygen uptake involves the measurement of oxygen uptake using sophisticated instrumentation during a graded exercise test to voluntary exhaustion in a controlled laboratory environment. Such conditions are difficult to justify/replicate on a routine basis, hence the interest in using 'indirect' or estimates of CRF, the most popular assessment of which are scores, or performance values, on the 20-m shuttle run test (20m SRT). The 20 metre shuttle run test is also known as the 'multistage fitness test' ('bleep' test) in the UK and as the 'PACER' (Progressive Aerobic Cardiovascular Endurance Run) test in the US. Since it was first reported as an alternative indoor test of cardiorespiratory endurance [6] the 20 metre shuttle run test has gained global popularity for monitoring fitness levels of athletes [2] and as a screening tool for CRF for individuals of all ages [7].
A recent meta-analysis concluded that the shuttle run test provided a useful alternative for estimating CRF with the performance score on the 20m SRT being a strong estimate of CRF in adults [8]. The latter study was reinforced by Castro-Pinero, et al. [9] who provided ('strong') evidence suggesting the 20mSRT was valid for estimating cardiorespiratory fitness in healthy adults aged 19-64 years of age.
For screening and monitoring estimated values for CRF need to be both valid and accurate [10]. Therefore the purpose of the present study was to investigate the validity of different models of estimated CRF values derived from 20m SRT performance with their corresponding directly measured values.
The current report uses data from cross-sectional studies that measured cardiorespiratory fitness as the maximum aerobic power ( ml kg-1 min-1) during exhaustive treadmill exercise and in parallel determined 20m SRT performance as the final shuttle run speed attained in the test (km h-1) [11-13]. These latter studies directly measured using either Douglas bag technology [12,13] or a metabolic cart system [11]. The tread mill test and 20m SRT were performed in no particular order, all that was requested from participants was to provide a 'maximum effort' on the day to the test in question. In total, from these three earlier studies, there were 178 participants (Men; n = 89; age, 22.8 ± 4.2 (range 18 to 42) years; height, 1.80 ± 0.07 m, body mass, 79.8 ± 12.4 kg; Women; n = 89; age, 21.3 ± 2.4 (range 18 to 31) years; height, 1.67 ± 0.06 m, body mass, 62.6 ± 9.3 kg). Each study received approval from the respective University Ethics Review Committee (s) and participants were treated in accordance with the principles laid down in the Declaration. The purpose, benefits and potential risks, of each study was explained and each participant signed a particular written Statement of Informed Consent.
Directly measured values were compared with predicted (estimated) values derived from three models; two earlier linear models (using linear regression equations) and a recent model based on allometry [1]. The model originally proposed by Léger, et al. [14] to predict was given by
(ml.kg-1.min-1) = 31.025 + 3.238·S − 3.248·A + 0.1536·A·S, (Eq. 1)
Where: S = 20m SRT run speed (km h-1) and A = age (in years). The authors claimed the model was appropriate for both boys and girls and that the same equation could be used for adults, keeping age constant at 18 years. The model proposed by Ramsbottom and co-workers, published in the same year [15], to estimate aerobic fitness in a physically active adult population (age range18 to 38 years) was of the form:
(ml.kg-1.min-1) = 14.4 + 3.48·x (Eq. 2)
Where: x = final shuttle level attained (effectively speed) on the 20m SRT.
In an allometric model proposed by Nevill, et al. [1] the equation was:
Ln (ml.kg-1.min-1) = -0.133 x Ln(M) + 1.519 x Ln(S) + 0.854 - 0.104 x female -0.16 x adult (Eq. 3)
Where : M = Mass and S = 20m SRT run speed (km h−1) and sex (“female”) and age (“adult”) were coded as male = 0 and female = 1 and adult =1 (equation 7 in Nevill, et al. [1].
Both linear regression equations underestimated the treadmill measured values, in contrast the allometric equation provided much closer estimates to the directly measured values (Table 1).
There was less bias associated with the allometric model and the 95% CIs were much closer (Table 1; Figure 1).
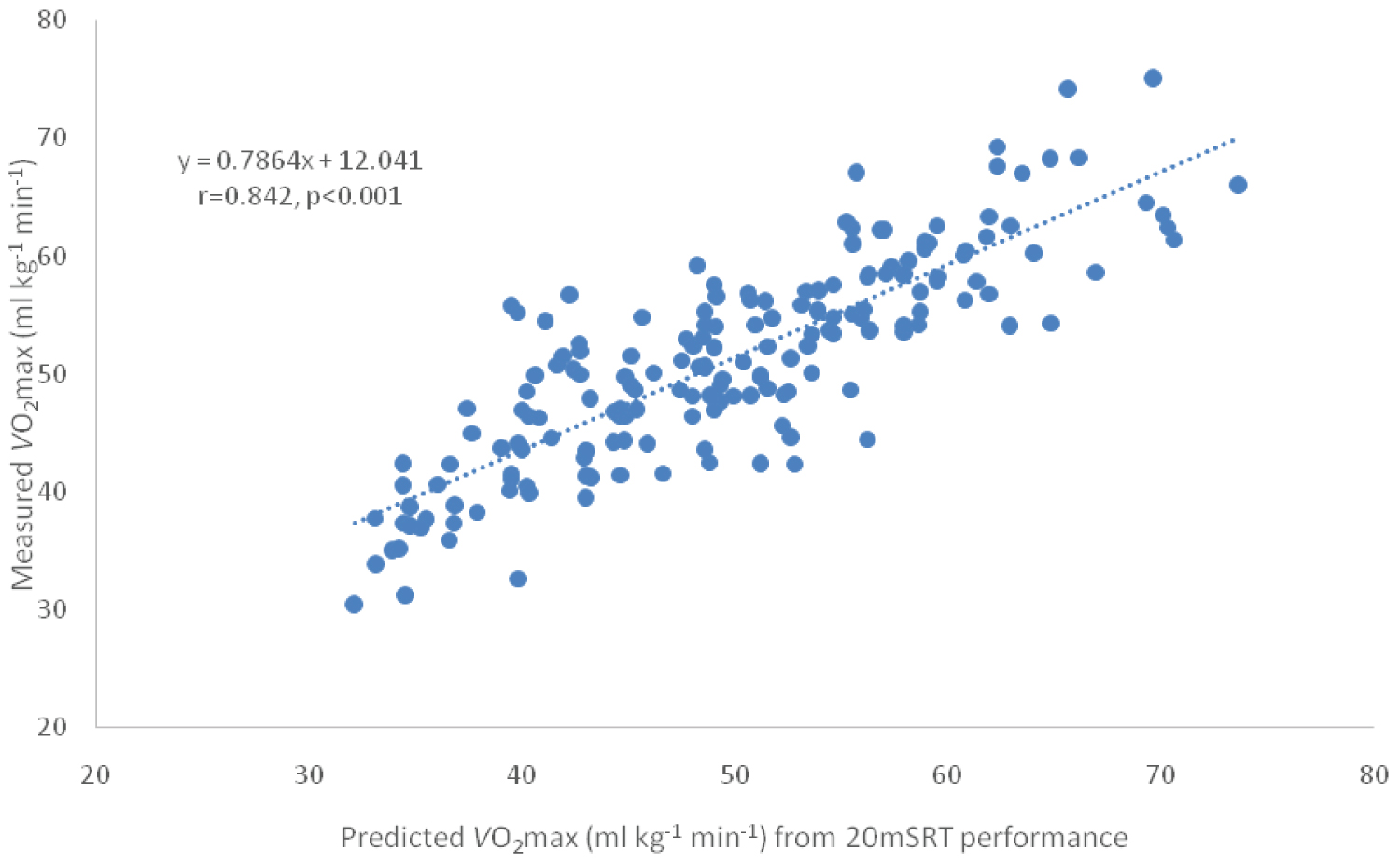 Figure 1: Data shown for the present study (n = 178) with directly measured O2max values plotted on the y axis against predicted (estimated) values on the x axis – values calculated from Equation 3 (above).
View Figure 1
Figure 1: Data shown for the present study (n = 178) with directly measured O2max values plotted on the y axis against predicted (estimated) values on the x axis – values calculated from Equation 3 (above).
View Figure 1
Table 1: Directly measured and predicted values (from 20m shuttle run test performance), bias and confidence intervals for the three models. View Table 1
When the directly measured values were plotted against shuttle run test performance (20m SRT speed; km h-1) a slight curvature in the data was observed (Figure 2).
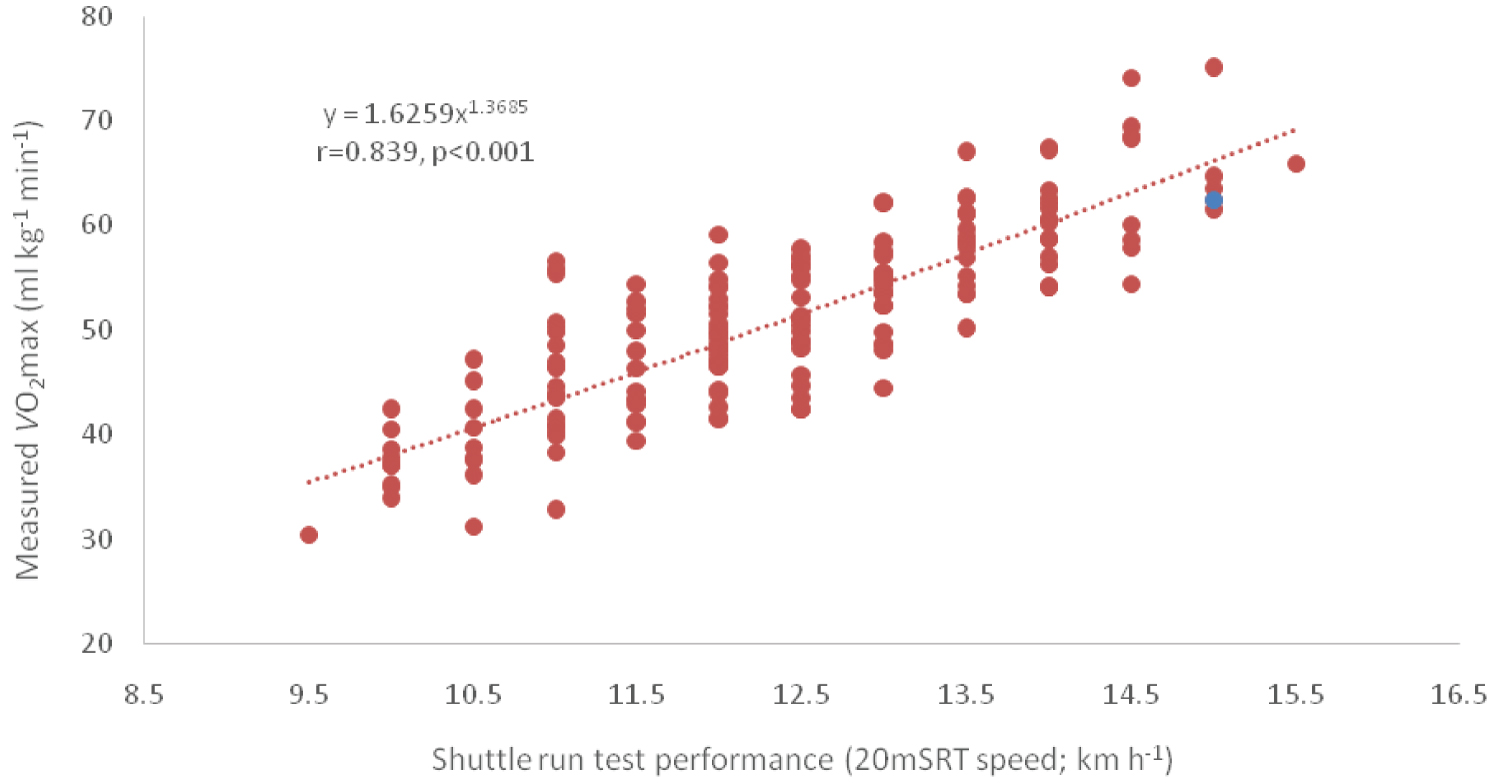 Figure 2: Data shown for the present study (n = 178) with treadmill measured O2max values plotted on the y axis against 20 metre shuttle run performance (20m SRT; km h-1) on the x axis.
View Figure 2
Figure 2: Data shown for the present study (n = 178) with treadmill measured O2max values plotted on the y axis against 20 metre shuttle run performance (20m SRT; km h-1) on the x axis.
View Figure 2
Over time many variations of the original Léger equation [14] have been developed, including some versions based on differences in ethnicity [16,17] although all models were based on linear regression. Of the three models under consideration in the present study the allometric model provided the closest predictions for the directly determined (that is provided greater accuracy) with a bias of only 1.4 compared with 6.8 and 4.4 ml kg-1 min-1 for the Ramsbottom, et al. [15] and Léger, et al. [14] equations respectively.
The slight curvature in the measured versus shuttle run test performance (km h-1) (Figure 2) reinforced the original observation reported by Nevill, et al. [1] namely that curvature reflects the increased energy demands of deceleration, coming to a virtual halt, turning through 180 degrees and then accelerating to the appropriate shuttle run speed demanded by the 20m SRT as the test progresses. Thus the curvilinear relationship shown in their mathematical model [1] actually reflects the physical and physiological demands of the 20m SRT, which was lacking in earlier linear models and / or predictive equations. The 20m SRT is practical, readily understood and used internationally to estimate CRF [18]. To go hand-in-hand with the latter observations a validated and accepted model is required for the prediction of CRF (ml kg-1 min-1) for the purpose of standardization. The data required for predictive CRF values, based on the allometric equation proposed by Nevill, et al. [1], are simple identifiable measures; final shuttle run speed, body mass and sex. Given the evidence provided by the present study the predictive values for CRF based on allometry [1] could be used for this purpose, as the allosteric model is less likely to underestimate CRF (ml kg-1 min-1) compared with the predicted values provided by the evaluated linear regression models.
An allometric model (Eq. 3 and Figure 1) provides more accurate and valid predictions of CRF ( ; ml.kg-1.min-1) in young adults compared with both the tested linear regression models.
Ethical clearance was provided by the local Ethics Committees of Northern Illinois University and Oxford Brookes University.
The authors would like to thank all participants who gave so willingly of their time and to be involved in experiments that led to temporary physical exhaustion.
AMN conceived the study and analyzed the data. RR drafted the manuscript, SP and RR designed their respective studies, directed implementation and data collection. RR, AMN and S Pedited the manuscript for intellectual content and provided critical comments on the manuscript.
No financial support was received for the conduct of this study or preparation of this article.
Roger Ramsbottom, Alan Nevill and Sharon Plowman have no conflicts of interest that are directly relevant to the content of this article.
Data are available on request.