The classification of metatarsus adductus by Bleck relied on the heel bisector line (HBL). The original procedure for bisecting the heel involves the initial making of a mould of the weight bearing foot to create an ellipse image of the heel. The procedure was later simplified by using photocopies of the foot instead of moulds of the foot. In either case, the heel is then bisected to determine its longitudinal axis which is designated as the HBL. The procedure for determining the longitudinal axis of the heel in Bleck's method is unclear and fraught with potential geometric errors. This paper presents an analysis of the said geometric errors in HBL and proposes the bisection of the transmalleolar axis as a geometrically accurate alternative to the HBL to be used for the clinical assessment of metatarsus adductus.
Geometry, Heel bisector line, Metatarsus adductus, Transmalleolar axis bisector
Metatarsus adductus is the medial deviation of the forefoot relative to the hindfoot. The classification of metatarsus adductus severity by Bleck [1,2] relied on the heel bisector line (HBL). The original procedure described by Bleck [2] for bisecting the heel involves the initial making of a mould of the weight bearing foot to create an ellipse image of the heel. The procedure is then completed by determining the longitudinal axis of the ellipse with a straight edge, independent of the forefoot (Figure 1). This method of bisecting the heel has been utilised by clinicians for over 4 decades, with some modifications to the procedure such as the use of footprints [3] and photocopying the sole of the weight bearing foot [4].
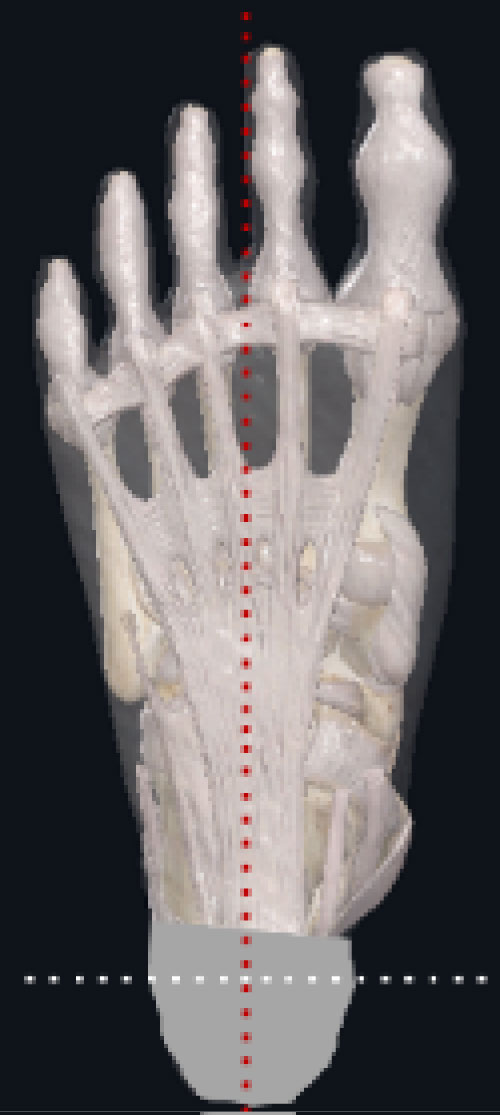Figure 1: Depiction of the Heel bisector line.
View Figure 1
Recent systematic reviews [3,5] show that the HBL is the most frequently used clinical and non-radiographic assessment of metatarsus adductus but its reliability and validity are yet to be evaluated. This paper explores the geometric inaccuracy of the HBL and proposes the Transmalleolar axis bisector (TMAB) as a geometrically accurate alternative.
Bleck's [1,2,6] original HBL method involved making a mould of the foot and isolating the heel from the rest of the foot in order to get an ellipse image before bisecting it. Smith, et al. [4] modified Bleck's method by determining the HBL from footprints made by photocopying the sole of the weight bearing foot. This procedure presents issues with the geometric accuracy of the HBLand its orientation relative to the forefoot because the heel in the footprint is not an ellipse but a partial irregular oval with undefined anterior boundary. The heel is part of a footprint which must remain intact in order to extend the HBL to see where it crosses the metatarsal heads. The mathematical definition of an ellipse does not apply to this partial oval. See Figure 2 in Smith, et al. [4].
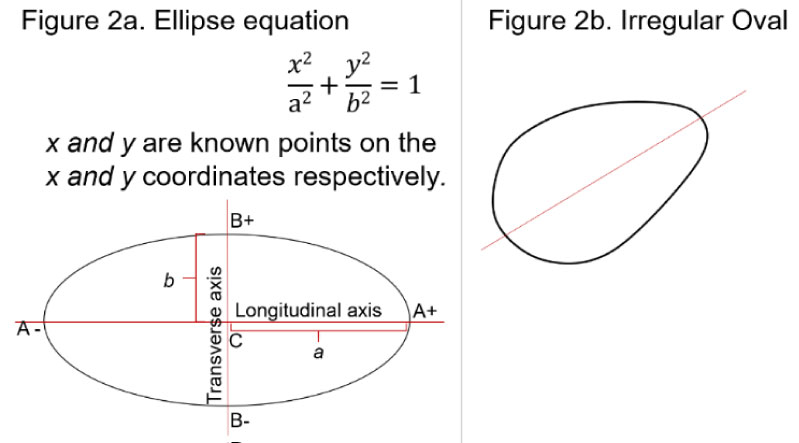Figure 2: The mathematical definition of an ellipse.
View Figure 2
An ellipse has a mathematical equation (Figure 2) that defines the location of its centre, boundaries and main axes, while an irregular oval does not [7-9]. The longitudinal and transverse axes of an ellipse mutually bisect each other at the centre of the ellipse. This mutual bisection of the axes is the defining feature of the 2 possible mirror symmetry of an ellipse. Conversely, an irregular oval has no mathematical definition and has only one axis of symmetry which makes it difficult to determine its centre and axis by applying the rules of coordinate geometry. It is worth noting that all ellipses are ovals but not all ovals are ellipses. An ellipse is a regular smooth oval with a mathematical definition. Irregular ovals may be smooth, but they have no mathematical definition. The partial oval formed by the heel print is irregular even if there was a way to define its entire boundaries (i.e. anterior pole) as in Bleck's original method. These facts therefore, demonstrate the uncertainty of the geometric accuracy of the Heel bisector line. See figure 19 in Bleck [1] and Figure 2 in Smith, et al. [4].
To determine the longitudinal axis of an ellipse with a compass and a ruler, one needs to follow the rules of coordinate geometry as depicted in Figure 3. (1) the lines (PQ and RS) bisecting two pairs of parallel chords on any points of the ellipse will intersect at the centre (C) of the ellipse. (2) The centre (C) of the ellipse is also the centre of a circle which intersects the boundaries of the ellipse at points A, B, D and E. (3) Points ABDE are the vertices of a rectangle (or a square depending on the size of the circle). (4) Bisecting either of the two shorter sides of the rectangle is a line that forms part of the longitudinal axis of the ellipse [7].
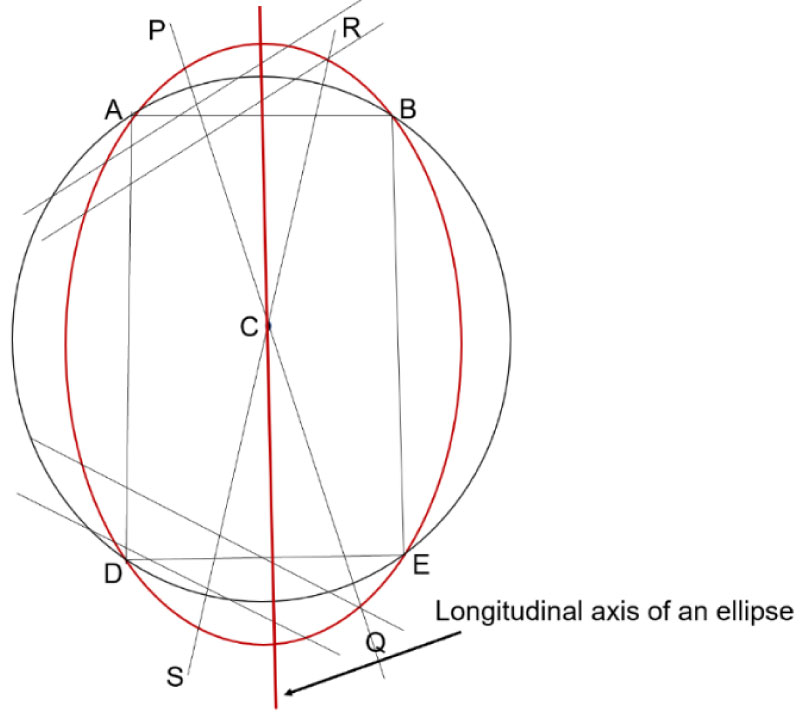Figure 3: How to determine the longitudinal axis of an ellipse with a compass and ruler. Not drawn to scale.
View Figure 3
The original HBL method by Bleck [1,2,6] mentioned the use of a straight edge (ruler) to determine the longitudinal axis of the ellipse, but using a compass was not mentioned. If Bleck's method included an implicit use of a compass, then it would be impossible to use this method on a footprint (or scan) on paper for the reasons given above, i.e. the heel print is not an ellipse but a partial irregular oval which has not mathematical definition and is not amenable to the rules of coordinate geometry.
The procedure for transmalleolar axis bisector (TMAB) is depicted in Figure 4. The patient is in prone lying with the knee of the lower limb of interest in 90° flexion. The assessor approximates the weight bearing posture of the foot by maintaining a plantigrade ankle joint. Then, with a pair of Vernier callipers, a line (AB) is drawn on the heel, linking the most medial point (A) on the medial malleolus to the most lateral point (B) on the lateral malleolus. Before dispensing with the Vernier callipers, the assessor must also mark the midpoint (C) on the line AB. The final part of the procedure is to use a goniometer on the heel with the axis on point C, the stationary arm aligned with line AB and the movable arm of the goniometer at 90° to the stationary arm. The movable arm of the goniometer thus becomes the TMAB i.e. a line perpendicular to and traversing the midpoint of line AB. The assessor finishes the procedure by checking the point at which the TMAB crosses the metatarsals heads. The outcomes may be recorded as; second interdigital web space (2nd IWS), third digit (3rd D), third interdigital web space (3rd IWS) etc. The TMAB depicted in Figure 4 crossed the metatarsal heads on the 4th digit. This is not intended to indicate population norm.
Figure 4: Transmalleolar axis bisector (TMAB).
View Figure 4
The Root model of normal and abnormal foot functioning [10] is facing serious challenges from recent evidence [11,12] and its significance in clinical practice has become controversial. Some of the challengers of the Root model also recommend that clinical assessment of some foot deformities including forefoot alignment should not be done in the non-weight bearing position [11]. However, the variety of routine clinical scenarios include children and adults with severe disability who cannot assume the weight bearing posture. This demographic also needs to have their feet assessed clinically. The proposed TMAB procedure approximates the weigh bearing posture of the footbased on the balance between the hindfoot supination force and the forefoot pronation force of ground reaction in normal bipedal stance [12].
A question that might arise is: Why not bisect the calcaneum with the Vernier callipers and a goniometer instead of using the malleoli as anatomical landmarks? The answer to this question is the geometric certainty of points A and B. Without which the orientation of a calcaneal bisector relative to the forefoot will be arbitrary with an unknown margin of error similar to the HBL.
The TMAB described in this paperis similar to the HBL in that it is non-invasive, and it requires minimum instrumentation. The TMAB however has theoretically, a greater construct validity than the HBL because important aspects of the construct of the heel bisector line are: (i) The exact determination of the boundaries of the so called ellipse contested in this paper to be a partial irregular ovaland (ii) The application of coordinate geometry rules. In the absence of one or both of these aspects of the construct, the orientation of the HBL relative to the forefoot would be arbitrary, with an unknown margin of error. This level of imprecision suggests that the use of theHBL has depended on the experience of the clinicians rather than procedural precision [13]. Conversely, the TMAB is geometrically accurate and easily replicable. These features of the TMAB will pave the way for reliability and validity evaluations of the method and the determination of normative values.
Bleck's classification of metatarsus adductus is based on a normative HBL defined as passing through the 2nd IWS. The rationale for this population norm was that, of the 2000 children's feet that Bleck studied, 85% of all the normal ones had an HBL that crossed the metatarsal heads at the 2nd IWS. The TMAB is very different from the HBL, hence it would be inappropriate to assume that the TMAB will have identical normative value to the HBL. Therefore, a very important next step is a normative study to determine population norms. The normative study is expected to be concurrent with reliability and validity evaluations. The determination of population norms for the TMAB may also be instrumental in developing a validated clinical scale for metatarsus adductus.
The author acknowledges Dr. Johanna Johannsson and Dr. Matthias Loeckx of LUNEX International University of Health, Exercise and Sports, Luxembourg for helping with Figure 4.
The author has no conflict of interested to disclose.
This article did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.
Victor O Alonge is the sole author of this article.