Climate change has a high impact on health and morbidity/mortality in respiratory system diseases and remains poorly investigated in probability distribution modeling. The objective of this study was to analyze the adjustments of Burr (Bu), Inv Gausian 3P (IG3P), Lognormal (LN), Pert (Pe), Rayleigh 2P (Ra 2P) and Weibull 3P (W3P) distributions of the historical series of hospitalizations for respiratory diseases (total hospital admissions) for the period from 2004 to 2018, in Campo Grande, MS. For the data series, the shape and scale parameters of the distributions were determined to verify the quality of fit of the observation data, the Goodness-of-Fit Tests (GOF): Kolmogorov-Smirnov Test, Anderson -Darling Test, Chi-square Test tests were used to verify an optimal estimate for the hospitalization data hospital.
All PDFs are able to describe well the characteristics of hospitalizations. The results presented (total admissions), (summer) show that the functions Weibull 3P (W3P) and Inv Gausian 3P (IG3P); (fall) show that the functions Burr and Weibull 3P (W3P); (winter) shows that the Burr and Inv Gausian 3P (IG3P) and (spring) functions for lognormal and Rayleigh (2P) functions provided the best observed fit for hospital admissions.
Hospital admission, Pneumonia, Modeling, Probability, Child and adults
Several studies of adjustment of probability density distribution or probability estimates using theoretical models of probability in relation to a historical series of data have been developed, highlighting the benefits in the planning of activities that minimize the risks, among which can be cited: precipitation [1-18], air temperature [19-22], solar radiation [20], concentration of pollutant gases [23,24], for the historical series of hospital admissions for respiratory diseases there are no published works with this methodology.
The use of probability density functions is directly linked to the nature of the data to which they relate. Some have good estimation capacity for small numbers of data, others require a large number of observations. Due to the number of parameters of your equation, some can take different forms, being framed in a greater number of situations, that is, they are more flexible. Since respecting the aspect of data representativeness, the estimates of its parameters for a given region can be established as general purpose, without prejudice to the precision in the estimation of probability [4].
Climate change has become one of the most serious environmental concerns for urban areas in recent decades. Several epidemiological studies in recent years have reported associations between high levels of climatic changes and increased rates of death and hospitalization for respiratory and cardiovascular diseases [25-31]. Some epidemiological studies show that air pollution affects human health, even concentrations of air pollutants are below the air quality standards [32-34].
Respiratory diseases and related mortality have been increasingly associated with exposure to climate change. Sensitive and vulnerable groups, such as pregnant women, children, the elderly, and those who already suffer from respiratory illnesses and other serious diseases, or from low-income groups, are especially affected by climatic variation. Studies have shown that the number of respiratory diseases in children and the elderly increases due to the higher concentrations of air pollution [35-41]. According to these studies, children are more susceptible because they need twice the amount of air inhaled by adults, and the elderly are more affected because of their weakened immune and respiratory systems and have been exposed to a large amount of air pollution in all your life.
In this study, we focused on determining the best statistical model that describes the number of hospitalizations for the city of Campo Grande.
Data on the number of hospitalizations for respiratory diseases were used, referring to the period from 2004 to 2018 of Campo Grande-MS, whose geographic coordinates are: 20° 27S; 54° 37W; 530 m and an estimated population of 850,000 inhabitants.
For the correlation of the meteorological data with the aggravation of respiratory diseases, data of hospital admission were collected, together with the health departments of the Department of Informatics of the SUS - Unified Health System (DATASUS).
The data available came from the Hospital Information System of SUS (SIH/SUS), managed by the Ministry of Health, through the Health Care Secretariat, in conjunction with the State Health Secretariats and the Municipal Health Department, and processed DATASUS, of the Executive Secretariat of the Ministry of Health.
The hospital units, participants of the SUS (public or private parties), send the hospitalization information, made by the AIH-Hospital admission authorization, to the municipal managers (full management) or state (the others). This information is processed in DATASUS, generating the credits related to the services provided and forming a valuable database, which contains a large part of hospital admissions, carried out in Brazil.
It should be noted that the SIH/SUS collects variables related to hospitalizations: Identification and qualification of the patient, procedures, examinations and medical acts performed, diagnosis, reasons for discharge, amounts due, etc. Through the Internet, DATASUS provides the main information for tabulation on the databases of the SIH/SUS.
This is an ecological study of time series. This type of design is characterized by studying groups of individuals, generally by geographic regions. In the case of this work the site studied is the city of Campo Grande-MS.
The study population was made up of people living in the city of Campo Grande who were hospitalized due to diseases of the respiratory system from 2004 to 2018. We analyzed all hospitalizations with diagnosis of respiratory diseases from all hospitals, to the Unified Health System (SUS). These data are records of the Hospital Hospitalization Authorizations (AIH) of public and private hospitals and that serve the portion of the population that does not have private health plans, private or funded by companies (http:/www.datasus.gov.br ). The information in the database is: The number of the Taxpayer's Registry (CGC) of the hospital, the city where it is located, the age of the patient, sex, cause of hospitalization, procedure performed, patient's postal code, hospitalization, date of discharge or death, days of UTI stay, among other information. Among the information in the database were selected for this study the date of hospitalization, the diagnosis, the age of the patient.
In this study, a descriptive analysis of the variables was performed, we used the Burr (Bu), Inv Gausian 3P (IG3P), Lognormal (LN), Pert (Pe), Rayleigh 2P (Ra 2P) and Weibull 3P (W3P) functions to model hospital admission data in Campo Grande. Performance indicators are calculated by comparing observed values to predicted values. The observed values are the classified values of the observation data, while the predicted values are the values obtained from the adjusted distribution.
In this study, the efficacy of six probability distributions of a component is evaluated. We use the parametric probability distribution functions (pdfs) of a component because our data have a unimodal distribution. These six models were selected among other models of a component because of their successful applications according to the literature.
The GOF is used to determine the best model among the distributions tested in the characteristic of hospitalizations for respiratory diseases. The goodness of fit test is performed to test the following hypothesis:
H0: The amount of monthly hospital admission data does not follow
H1: The amount of monthly hospital admission data does not follow a distribution
A couple of goodness-of-fit test have been conducted such as Kolmogorov-Smirnov test, Anderson-Darling test along with the chi-square test at significance level (α = 0.05) for choosing the best probability distribution [42].
The Kolmogorov-Smirnov test [43] is used to decide if a sample comes from a population with a specific distribution.
The Kolmogorov-Smirnov (K-S) test is based on the empirical distribution function (ECDF). Given N ordered data points Y1, Y2, ..., YN, the ECDF is defined as
Where n(i) is the number of points less than Yi and the Yi are ordered from smallest to largest value. This is a step function that increases by 1/N at the value of each ordered data point.
The Kolmogorov-Smirnov test statistic (D) is defined as
Where F is the theoretical cumulative distribution of the distribution being tested which must be a continuous distribution (i.e., no discrete distributions such as the binomial or Poisson), and it must be fully specified (i.e., the location, scale, and shape parameters cannot be estimated from the data).
The hypothesis regarding the distributional form is rejected if the test statistic, D, is greater than the critical value obtained from a table.
The Anderson-Darling test (Stephens, 1974) is used to test if a sample of data comes from a population with a specific distribution. It is a modification of the Kolmogorov-Smirnov (K-S) test and gives more weight to the tails than does the K-S test. The K-S test is distribution free in the sense that the critical values do not depend on the specific distribution being tested. The Anderson-Darling test makes use of the specific distribution in calculating critical values. This has the advantage of allowing a more sensitive test and the disadvantage that critical values must be calculated for each distribution. Currently, tables of critical values are available for the normal, lognormal, exponential, Weibull, extreme value type I, and logistic distributions.
The Anderson-Darling test statistic (A) is defined as
F is the cumulative distribution function of the specified distribution. Note that the Yi are the ordered data. The critical values for the Anderson-Darling test are dependent on the specific distribution that is being tested. Tabulated values and formulas have been published [44] for a few specific distributions (normal, lognormal, exponential, Weibull, logistic, extreme value type I). The test is a one-sided test and the hypothesis that the distribution is of a specific form is rejected if the test statistic, A, is greater than the critical value.
The Chi-square test assumes that the number of observations is large enough so that the chi-square distribution provides a good approximation as the distribution of test statistic. The Chi-squared statistic is defined as
Where Oi is observed frequency, Ei is expected frequency, 'i' is number observations (1, 2, ......k), calculated by Ei= F(X2) – F(X1), F is the CDF of the probability distribution being tested.
The observed number of observation (k) in interval 'i' is computed from equation given below
Where n is sample size.
This equation is for continuous sample data only and is used to determine if a sample comes from a population with a specific distribution [42].
Figure 1 illustrates a typical pattern of hospital admissions (morbidity) for respiratory diseases, the average of the months of the years 2004 to 2018, as an example of a typical pattern.
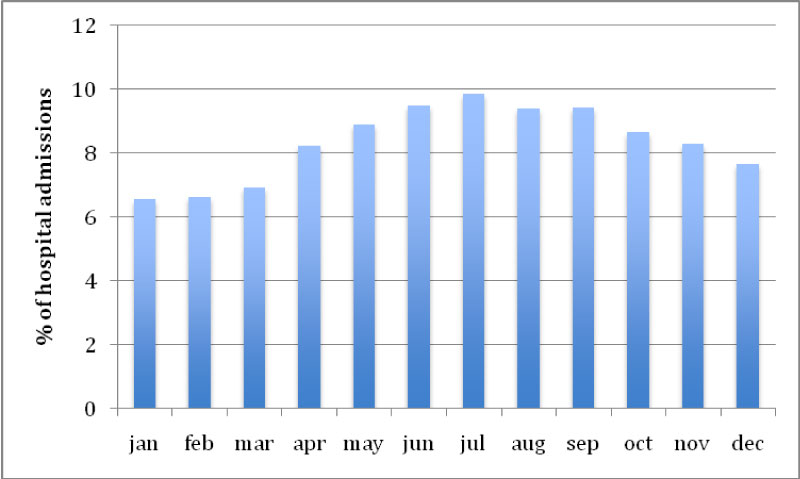 Figure 1: Monthly percentage of respiratory disease morbidity (DAR) in the years 2004 to 2018.
View Figure 1
Figure 1: Monthly percentage of respiratory disease morbidity (DAR) in the years 2004 to 2018.
View Figure 1
During the study period (January 1, 2004 to December 31, 2018) the number of hospitalizations for respiratory diseases was 63,316, with an average of 4221 hospitalizations per month, with a maximum number of hospitalizations from May to October (Table 1).
Table 1: Descriptive statistics of hospital admissions. View Table 1
Figure 1 shows the behavior of mean monthly admissions for respiratory diseases. According to the data, a seasonal pattern was observed between periods of rainfall, drought and transition, especially in the months (April, May, June, July, August and September), where the peak of hospitalizations corresponding to the dry season, low precipitation, relative humidity and minimum temperatures.
It is essential to recognize that social and economic factors play a significant role in predicting the change in the risk of infectious diseases caused by climate change [45-47]. Some populations and regions are more vulnerable to high risks because of their inability to respond effectively to the tensions and challenges posed by climate change [48-50]. Vulnerability levels are partly a function of the programs and measures implemented to reduce the burden of climate-sensitive health determinants and outcomes, and partly to the success of traditional public health practices, including access to safe and better drinking water, sanitation and biosafety and surveillance programs to identify and respond to outbreaks of infectious diseases [48,51-53]. The vulnerability of a society to climate change induced by the risk to the health of infectious diseases is related to its social development. Many infectious diseases often occur in developing countries after tropical cyclones, but are rare in developed countries [54].
The vulnerability of a society to climate change induced by the risk to the health of infectious diseases is even more related to the public health system and to the existing infrastructure. Developing countries tend to be more sensitive to a high health risk posed by climate change because of the lack of resources and capacities for their public health system to effectively respond to the various challenges. Vulnerability to changes in the risks of infectious diseases can be reduced by appropriate adaptation measures. Adaptation can be effective in addressing the challenges posed by climate change. It is important to emphasize that the success of a proactive adaptation depends to a large extent on the correct prediction of the change from the health risk scenario to infectious diseases.
Adaptation measures may be informed by better weather forecasts, including prediction of extreme weather events and weather hazards. By developing an early warning system based on accurate weather forecasts, a society can better prepare for the health risks related to climate change.
Souza and Santos [55] calculated hospitalizations attributed to heat and cold, defined as temperatures above and below optimal temperature and for moderate and extreme temperatures, defined using cutoff point the 2.5th and 97.5th percentiles. They analyzed 148, 849 admissions in several periods. In total, 6.62% (95% IC-6.53-6.82) was due to the non-optimal temperature. The percentile minimum morbidity temperature ranged from approximately the 60th percentile. The temperatures attributable to hospitalization were caused by cold (6.38%, 95% IC 6.04-6.58) rather than by heat (0.39%, 0.28-0.42).
Little evidence is available on the association between ozone exposure and health in Campo Grande, Brazil [56] examined the effects of surface ozone concentrations (O3) on respiratory morbidity in Campo Grande, Brazil. A Poisson time series model was used to examine the effects of O3 on hospital admissions, while controlling for seasonality, long-term trend, temperature, and relative humidity. A nonlinear distributed delay function was used for O3, temperature and relative humidity. We examined the effects of O3 in different age groups (0-4 years, 5-60 years and > 60 years). The relationship between ozone and respiratory morbidity was not linear, with a threshold of 13 ppb (less than 25% of the ozone distribution percentage). The relative risk of hospital admission at the 75th percentile of the O3 distribution compared to 25% of the O3 distribution percentile. The effect of O3 on respiratory morbidity was delayed by two days and lasted 4 days for all age groups, except for people between 5 and 60 years. Children and the elderly were much more vulnerable to ozone pollution than people aged 5 to 60. The study suggests that ozone pollution has negative impacts on respiratory diseases in Campo Grande, Brazil. Children and the elderly were susceptible to exposure to O3. These findings should be used to develop policies to protect people from O3 pollution.
When comparing this pattern with the burned indexes, it is observed an increase in respiratory attendance due to the fires, between August, September and October that compose the dry period of the year and intensification of the fires and higher concentration of fires [55-57].
The use of different methods may lead to inconsistent or even contradictory results. For example, in a study investigating the climatic effects of respiratory diseases in the city of Campo Grande, temperature accounts for a large part of the variance in a multivariate Poisson regression model [55]. However, using the same data source, but based on an integrated autoregressive mobile time series model, another study reported no significant association of temperature and hospital admissions with respiratory diseases. We must realize that a better understanding of the mechanisms of interactions requires the integration of methods with detailed monitoring. However, this has been rare in existing literature.
Among the diseases cataloged in the International Coding of Diseases (ICD 9a and 10a revisions) as respiratory diseases (460-496 and J00-J99 respectively), it was verified that the highest daily averages of hospitalizations were due to influenza and pneumonia (480-487 and J10-J18) representing 52.3% of all admissions. Second, chronic diseases of the lower airways, such as chronic bronchitis, simple and mucus-purulent bronchitis, emphysema, asthma, malaise asthmaticus and bronchiectasis (490-496 and J40-J47) with 19.3%. Third, with 11.3% and a daily average of 5.2, there were the other upper airway diseases (470-478 and J30-J39), such as allergic and vasomotor rhinitis, rhinitis, chronic nasopharyngitis and pharyngitis, chronic sinusitis, nasal polyp, other disorders of the nose and paranasal sinuses, chronic diseases of the tonsils and adenoids, chronic laryngitis and laryngotracheitis. Other acute lower respiratory infections (466 and J20-J22), such as acute bronchitis and bronchitis, which had a daily mean of 2.8 and accounted for 6% of all hospitalizations. Finally, acute upper respiratory infections (460-465 and J00-J06) accounted for 4.3% of hospital admissions, with a daily average of 2.0. These diseases were as follows: Acute nasopharyngitis (common cold), sinusitis, pharyngitis, tonsillitis, laryngitis, obstructive laryngitis, epiglottitis and tracheitis. The other diseases of the respiratory system did not reach 2.0 hospitalizations and had a very low percentage - except for the grouping of unspecified diseases (508 and J95-J99), which represented 4.9% of hospitalizations and a daily average of 2.2. However, this grouping, as its name implies, represents unspecified diseases and, therefore, it is not possible to know the actual cause of hospitalizations.
The parameters of the estimates of the tested distributions are presented in Table 2, these parameters are obtained 'using the Matlab software. Figure 2 shows, respectively, the histogram of the hospital admissions of hospitalizations of the years 2004 to 2018, adjusted by the six probability density functions studied and their cumulative frequency adjusted by the six functions of cumulative distribution.
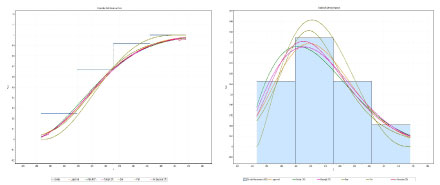 Figure 2: Graphs cdf (left) and pdf (right) of the distributions obtained for the monthly averages of hospital admissions for the years (2004-2018).
View Figure 2
Figure 2: Graphs cdf (left) and pdf (right) of the distributions obtained for the monthly averages of hospital admissions for the years (2004-2018).
View Figure 2
Table 2: Estimated parameters for the distributions studied. View Table 2
Table 2, Table 3, Figure 2 .
Table 3: Criteria for quality adjustment of the historical series of total hospital stays (2004-2018) for respiratory diseases, for the six distribution models Probability using different fit quality tests. View Table 3
Table 4, Table 5, Figure 3.
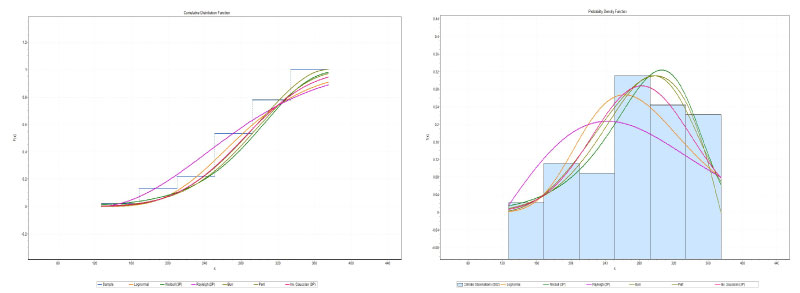 Figure 3: Graphs cdf (left) and pdf (right) of the distributions obtained for the monthly averages of hospital admissions for summer (2004-2015).
View Figure 3
Figure 3: Graphs cdf (left) and pdf (right) of the distributions obtained for the monthly averages of hospital admissions for summer (2004-2015).
View Figure 3
Table 4: Estimated parameters for the distributions studied. View Table 4
Table 5: Criteria for quality adjustment of the historical series of hospital stays for the summer (2004-2018) for respiratory diseases, for the six distribution models Probability using different fit quality tests. View Table 5
Table 6, Table 7, Figure 4.
 Figure 4: Graphs cdf (left) and pdf (right) of the distributions obtained for the monthly averages of hospital admissions for autumn (2004-2018).
View Figure 4
Figure 4: Graphs cdf (left) and pdf (right) of the distributions obtained for the monthly averages of hospital admissions for autumn (2004-2018).
View Figure 4
Table 6: Estimated parameters for the distributions studied. View Table 6
Table 7: Criteria for quality adjustment of the historical series of hospital stays for the autumn (2004-2018) for respiratory diseases, for the six distribution models Probability using different fit quality tests. View Table 7
Table 8, Table 9, Figure 5.
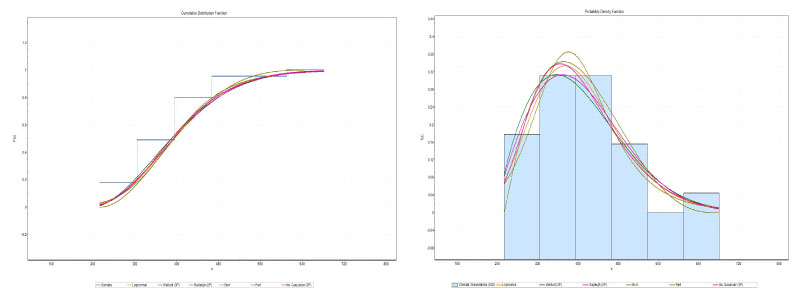 Figure 5: Graphs cdf (left) and pdf (right) of the distributions obtained for the monthly averages of hospital admissions for Winter (2004-2018).
View Figure 5
Figure 5: Graphs cdf (left) and pdf (right) of the distributions obtained for the monthly averages of hospital admissions for Winter (2004-2018).
View Figure 5
Table 8: Estimated parameters for the distributions studied. View Table 8
Table 9: Criteria for quality adjustment of the historical series of hospital stays for the Winter (2004-2018) for respiratory diseases, for the six distribution models Probability using different fit quality tests. View Table 9
Table 10, Table 11, Figure 6.
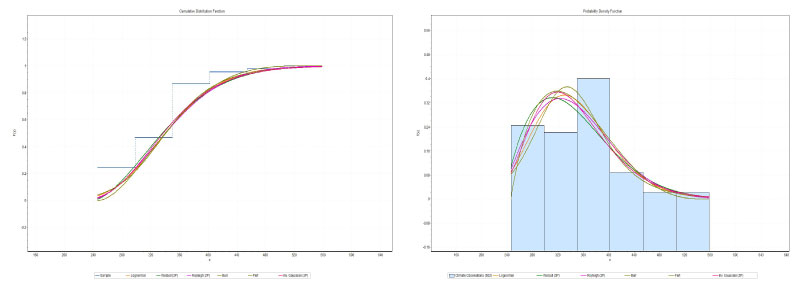 Figure 6: Graphs cdf (left) and pdf (right) of the distributions obtained for the monthly averages of hospital admissions for Spring (2004-2018).
View Figure 6
Figure 6: Graphs cdf (left) and pdf (right) of the distributions obtained for the monthly averages of hospital admissions for Spring (2004-2018).
View Figure 6
Table 10: Estimated parameters for the distributions studied. View Table 10
Table 11: Criteria for quality adjustment of the historical series of hospital stays for the Spring (2004-2018) for respiratory diseases, for the six distribution models Probability using different fit quality tests. View Table 11
The statistical parameters for assessing the suitability of the analyzed PDFs are presented in Table 3, Table 5, Table 7 and Table 9. All the PDFs are able to describe well the characteristics of the hospitalizations. The results presented in Table 3 (total hospitalizations) and Table 5 (summer) clearly show that the functions weibull 3P (W3P) and Inv Gausian 3P (IG3P), provided the best adjustment of hospital admissions observed. The results presented in Table 7 (autumn) clearly show that the Burr and Weibull 3P (W3P) functions provided the best hospital adjustment observed, Table 9 (winter) clearly shows that the Burr and Inv Gausian 3P (IG3P) functions, provided the best adjustment for hospital admissions observed. Table 9 shows that the Rayleigh (2P) and Burr functions provided the best hospital adjustment observed, Table 11 (spring) for the lognormal and Rayleigh (2P) functions, provided the best adjustment of the hospital admissions observed.
In Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6, we present the time series of hospital stays for the years 2004 to 2018. There is no clear variation or trend around an average value. To extract more information about the behavior of the series, Table 1 shows the calculations of mean, standard deviation, variance, asymmetry for the mean of the studied years. It is quite evident the lack of homogeneity in the data of each time series, because in all cases, it is observed that the standard deviation presents average amplitude and a very high variance. These facts are corroborated by the fact that these measurements are highly sensitive to atmospheric conditions, sudden physical changes at measurement sites, and other changes that make the series very heterogeneous and unpredictable in the long run. With regard to asymmetry, it is possible to notice a situation of asymmetry in all cases, with right or positive displacement.
The adjustment of the six functions of probability density was through the Kolmogorov-Smirnov test, Anderson Darling and Chi Squared. Table 2, Table 3, Table 4, Table 5, Table 6, Table 7, Table 8, Table 9, Table 10 and Table 11 presents the test results for the probability density functions that best fit the data as well as the parameter values of the models. In this table it is possible to compare the adjustment is approved according to K-S criteria. Approved functions are highlighted in the table. It is also possible to observe that all the adjustments approved by the tests presented very low values for the maximum quadratic error, corroborating, therefore, adjustments as being the best ones for the respective series.
Finally, the Figures shows the comparison of the adjustments of the best probability density functions with the respective original series (observed). By means of these figures it is possible to note again the trend with positive displacement of both the fitted models and the observed data. In addition, the small differences between the observed profile and the adjusted functions are more clearly demonstrated, because in this reconstruction, different from what happens with the accumulated frequency, the errors are no longer attenuated by the accumulation of frequencies, so that discrete discrepancies become, if clearer. Such discrepancies do not invalidate the results, since the representativeness presented by the models is larger than expected given the heterogeneity of the series.
The results show that all temporary series studied are able to describe hospitalizations well. The results (total admissions), (summer) show the functions Weibull 3P (W3P) and Inv Gausian 3P (IG3P); fall functions Burr and Weibull 3P (W3P); (winter) shows how Burr and Inv Gausian 3P (IG3P) and (spring) functions for lognormal and Rayleigh (2P) functions provide the best observed fit for hospital admissions.
Through the study, it can be concluded that all time series studied presented positive displacement asymmetry. Regarding the adjustment of the best probability distribution model, it was found that for each season a set of PDFs is satisfactorily adjusted.
All authors performed the data analysis, applied the model, created the figures and prepared the original draft, analyzed the raw data and revised the original draft, helped to collect the raw data from the monitoring station.
Climate change impacts human infectious disease via pathogen, host and transmission.
Go beyond empirical observation of association between climate and health effect.
Improve prediction of associated shifts in infectious diseases at various scales.
The health impacts may be controlled through adopting certain proactive measures.
Establish local early warning system for health effect of predicated climate change.
The meteorological database is public domain and is available at: Center for Monitoring Weather, Climate and Water Resources of Mato Grosso do Sul (Cemtec/MS), an agency linked to the State Secretariat of Environment, Economic Development, Production and Family Agriculture (Semagro), http://www.cemtec.ms.gov.br/laudos-meteorologicos/.
The ozone pollutant database belongs to the physics institute of the federal university of mato grosso do sul and may be requested from Prof Dr Amaury de Souza, e-mail: amaury.souza@ufms.br.
This research did not receive external funding.
The authors would like to thank their Universities for their support.
The authors declare no conflict of interest.