J Hypertens Manag ISSN: 2474-3690

• Abstract
• Keywords
• Introduction
• 0D Models
• 1D Models
• Conclusions
• Figure 1
• Figure 2
• Figure 3
• References

Download PDF
    

Journal of Hypertension and Management

¹Department of Mathematics, University of Ioannina, Greece
²Cardiovascular Surgery Department, Sector of Surgery, Faculty of Medicine, University of Ioannina, Greece

Abstract

The mathematical modeling of blood flow in the cardiovascular system has long history. Zero-dimensional (0D) and one-dimensional (1D) models contribute actively to the study of the human cardiovascular system. Usually, low-dimensional models consist of a system of time dependent equations that do not involve spatial derivatives, thus reducing the computational complexity compared to multi-dimensional models. Despite that more complex 3D cardiovascular models are available, there is a tendency of reintroducing the simpler 1D models, due to their capability of involving extensive segments of the cardiovascular system and providing boundary conditions for the advanced 3D models. The low-dimensional models can provide useful information to clinicians about the characteristics of blood flow at the level of individual incidents, patient-specific treatment, and can describe the general phenomena of circulatory physiology. The purpose of the current review is to discuss the advances and evolution of 0D and 1D models of human cardiovascular system.

Keywords

Mathematical modeling, Cardiovascular system, Blood flow, 0D models, 1D models, Computational methods

Introduction

The cardiovascular system is the blood transport mechanism that enables the nutrient transport to the tissues and organs of the body and the removal of various waste and toxic substances [1]. It includes the heart that pumps blood into circulation, the systemic blood vessels that drive blood to and from the peripheral organs, and the pulmonary vessels that enable the exchange of oxygen and carbon dioxide in the lungs. Blood is channeled from the aorta to the arteries, arterioles, capillaries, structuring an arterial tree with decreasing vessel diameters but increasing vessel luminal area overall, with the vessel wall becoming stiffer after consecutive branches.

Blood flow in the cardiovascular system obeys the laws of mass and momentum conservation and blood interaction with the arterial wall [2,3]. The selection of the appropriate model dimensionality, from 0D to 3D, depends on the aims and the desired accuracy. Lumped parameter models assume a uniform distribution of the fundamental variables, pressure, flow and volume, within any particular compartment, organ or vessel at any time instant. The higher dimensional models on the contrary account for the spatial variation of the fundamental variables as well. The distensibility and compliance of the arteries introduce additional constraints that strongly influence blood flow dynamics.

The 0D models give rise to a coupled system of ordinary differential equations (ODEs), suitable for the assessment of global distributions of pressure, flow and blood volume over a range of physiological conditions. For each vascular compartment included in the models, two ODEs are applicable, representing conservation of mass and momentum, complemented by an algebraic equilibrium equation that relates compartment volume to pressure. On the other hand, 1D models are based on simplified fluid flow equations that are solved in the frequency domain using Fourier or Laplace transformations [4-10]. The 1D models are well balanced with respect to modeling complexity and computational cost, rendered suitable for many biomedical applications. With the 1D models, it is possible in the near future to have fast, accurate, patient-specific and clinically applicable solutions for the dynamic flow prediction in the whole human cardiovascular system [11].

The mathematical models of blood flow, with their given noninvasive character, facilitate the study of pathological and physiological waveforms. It is strongly believed that the computation of pressure and flow profiles could be part of potential diagnostic tools in the future. On a patient specific basis, the profiles could be compared with physiological ones suggesting healthy or pathological blood flow.

0D Models

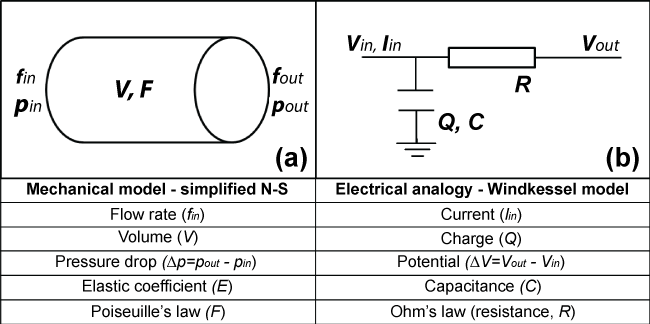
Blood flow in the circulatory system and electrical conductivity in a circuit have shared characteristics and analogous abstract interpretation. Blood pressure in the circulatory system is the reason that blood flow overcomes the hydraulic resistance. Similarly, voltage in a circuit is the reason that current flow overcomes the electrical resistance. The hydraulic resistance represents the combined effect of the cohesive forces, due to the wall elasticity, and blood inertia, while the electric resistor represents the combined resistance in the circuit. Blood flow is described by the conservation of mass (continuity equation) and conservation of momentum (Navier-Stokes equations). Similarly, the electrical flow in the circuit is governed by Kirchhoff's and Ohm's law for the current and voltage, respectively. The equation in the mechanical system associated with the vessel wall distensibility is related to the equation for the capacitor. Figure 1 shows the mechanical model (Figure 1a), e.g. a straight elastic tube, the electrical model (Figure 1b), e.g. a resistance-capacitor (RC) circuit, and the associated unknown quantities that have uniform physical interpretation. The simplest 0D model of the cardiovascular system is based on the famous Windkessel model (Figure 1b).

One-compartment and multi-compartment 0D models

In one-compartment models, the whole systemic vasculature is treated as a whole, and thus the internal pressure distribution and flow velocity in different parts of the vascular network are not calculated separately. The 2-Elements Windkessel model (Figure 1b) is the simplest 0D model consisting of a capacitor (C) that represents the compliance of the large arteries, and a resistor (R) that represents the resistance of small peripheral arteries including arterioles and capillaries [12-18]. The introduction of an extra resistor in series with the existing RC extended the applicability of Windkessel models, accounting for the resistance of the aortic valve to blood flow [19]. The 3-Elements Windkessel model simulates the characteristic impedance of the proximal aorta and is widely used for assessing cardiovascular function in various pathophysiological states. Other studies further extended the RCR model by integrating the inertial effect of blood flow, forming a RLCR circuit. The 4-Element gives a more accurate representation of blood pressure with cardiac cycle time compared to the 2- and 3-Elements models.

Using one-compartment Windkessel models as building blocks, multi-compartment models provide more spatial details by including multiple vascular segments [20-25]. Other parts of the cardiovascular system may still be considered lumped, using less detail. For the construction of a multi-compartment model, appropriate RLC models are created for each represented part of the whole network [26-33]. Burattini and Natalucci [34] developed a different configuration introducing three RCR elements to describe the characteristics of the arterial system, accounting for the viscoelastic properties of the vessel wall. More complex models can also incorporate additional parameters, such as pulse in venous pressure and flow in the components.

A special case of 0D modeling is that of local circulation characteristics in important vascular subsystem, such as cerebral, coronary, renal or lower extremity vessels where often multiple compartment models have been designed to include features such as anastomoses, auto-regulation effects and occasionally collapsible vessels and internal valves. Most commonly, these local simulations do not include a heart model, and usually flow rates and pressures are directly applied as boundary conditions [35-43].

A model consisting of a series of 0D compartments is a representation of a 1D system. Milisic and Quarteroni have given a mathematical proof that 0D models for the vessel network can be regarded as first order discretizations of 1D linear systems [44]. Such models are readily interpreted in terms of electrical analogues. The biggest difference between multiple linear 0D compartment models and published 1D models is that the latter tend to include the nonlinear convective acceleration term whereas the former cannot [45].

0D heart models

There have been numerous studies on the qualitative characterization of the heart as a pump. Due to double contraction and expansion of the left and right heart regions can be said that heart is a two pump system, connected together in series. Despite the similarity of these two pumps most studies examined the properties and functioning of one pump, usually the left one. Many researchers have discussed the characteristics of the left ventricle, to examine whether it should be described as a pressure or a flow source [46]. The atrial-ventricular interaction was also considered to be important in cardiovascular dynamic studies. In these studies, the effect of the pericardium on the cardiac dynamics was included in the analysis [20,22,26-33,47]. It is worth noting that the atrial-ventricular septum motion contributes about 10% of the cardiac output as it undergoes large displacements during the cardiac cycle. Korakianitis and Shi have derived detailed equations to model the motion of the septum [28,29]. Further developments in modeling heart dynamics in the cardiovascular network include multi-scale and multi-physics models of the cardiac function [48] and the coupling of lumped-parameter and distributed network models for cerebral pulse-wave hemodynamics [49]. Recently, there has been effort to develop 1D model of the entire cardiovascular system that includes anatomically realistic 1D vascular network in all major regions of the circulation, coupled to a 0D heart model that accounts for the main chamber interactions [50].

The simplest heart valve models used in 0D studies of cardiovascular dynamics described valves as a diode plus a linear or non-linear resistance. The valve has a low resistance to flow when fully open, and the flow is stopped completely when the valve is closed. This idealized description ignores more complex dynamics of the valve, but can be considered adequate for most studies [46].

Auto-regulation mechanism

When blood is pumped from the heart, and the pressure in the aorta is increased, then the aorta expands. When the pressure drops, the aorta is retracted so that the flow rate through the small peripheral vessels does not immediately go to zero. The acute increase in blood pressure causes an immediate increase in blood flow. However, in most tissues pressure returns to normal level, even if the blood pressure remains high. This restoration of flow to the normal mode is called automatic regulation. The detailed underlying mechanism of auto-regulation is unknown, but the metabolic requirement of the organ and the myogenic response of the vascular smooth muscle are considered to be two of the main causes [51]. Auto-regulation has an important influence on the blood flow in several local circulation loops, including the cerebral, renal, and hepatic circulations, and is an important component of any model of these subsystems [52-55]. Several mathematical models of auto-regulation mechanism have been proposed [41,43,55,56]. In these studies, Ursino and collaborators have proposed a comprehensive mathematical model of intracranial dynamics and cerebrovascular regulation. The results of this mathematical model were correlated with transcranial doppler (TCD) ultrasonography, an approach that is largely used today to achieve non-invasive assessment of cerebral autoregulation and cerebrovascular reactivity in neurosurgical patients.

1D Models

Propagation of pressure and flow waves in the vessel network is one of the most interesting problems in the study of cardiovascular physiology. It is generally believed that important information regarding cardiac function, the elastic properties of the vessels, and the pathophysiological conditions of the important organs, such as brain, liver and kidney, is implemented in these two wave forms and their relationship. Pulse wave studies have received extensive attention in cardiovascular research [57]. To this direction, 1D modeling can offer greater advantages in revealing the pressure and flow changes along the whole length of the studied vessel.

Due to the fact that the vascular system includes billions blood vessels, these 1D numerical models must be truncated and appropriate outflow boundary conditions have to be specified [58]. Additionally, these numerical models can be terminated at a level where the nonlinear losses are minor and linear models could describe flow velocity and pressure waves.

Numerical and analytical methods for 1D models

For the development of 1D mathematical models of the vascular system, the nonlinear 1D wave propagation method offers a good compromise between anatomic accuracy, inclusion of nonlinear losses and material properties. The 1D wave propagation method involves solving the governing equations of blood flow in a 1D domain and is based on the assumptions that the dominant component of blood flow velocity is oriented along the vessel axis and that pressure can be assumed constant over the cross-section of the vessel. The derived governing equations for the 1D pulse wave propagation have a hyperbolic nature [59]. A simplified system of equations that describes the 1D interaction of blood with the arterial tissue, as proposed by Olufsen et al. [9], is shown below:

Continuity Equation,

$\frac{\partial q}{\partial x}+\frac{\partial A}{\partial t}=0\text{ (1)}$

Momentum Equation,

$\frac{\partial q}{\partial t}+\frac{\partial }{\partial x}\left(\frac{q^2}{A}\right)+\frac{A}{\rho }\frac{\partial p}{\partial x}=-F\text{ (2)}$

State Equation, (distensibility)

$p\left(x,t\right)-p_0=\frac{4}{3}\frac{Eh}{r_0}\left(1-\sqrt{\frac{A_0}{A}}\right)\text{ (3)}$

where q is the flow through the vessel, A, is the cross-sectional area, $F=\frac{2\pi \nu R}{\delta }\frac{q}{A}$ is the Poiseuille's term, ρ is the blood density, E is the Young's modulus, the term $\frac{Eh}{r_0}$ is evaluated from an exponential expression.

Another approach is based on Womersley's solution for pulsatile flow in an elastic vessel [60]. Under the assumptions of axisymmetry, linear constitutive behavior, and small perturbations about a constant pressure and zero axial velocity reference state, a system of linear partial differential equations (PDEs) governing the fully developed pulsatile flow in an elastic vessel can be derived and solved analytically. For a prescribed input flow rate, the Fourier coefficients of the input pressure can be determined. An inverse Fourier transform can be used to compute the inlet pressure. Pressure and flow rates throughout the vascular tree can be computed by enforcing conservation of mass and continuity at branch points [61]. While impedance based linear methods can be used to describe pressure and flow wave propagation in vessels, these models do not incorporate non-linear convective losses or losses due to branching and stenoses [62-64]. This is the most significant limitation of Womersley's elastic vessel theory, especially as applied to blood flow in the main arteries and in the diseased state. Recent approaches, as the total variation diminishing (TVD) scheme have been proposed to solve 1D blood flow for human circulation. This method involves only a few modifications to existing shock-capturing TVD schemes. For 1D network simulations, the method has been shown to agree well with computational results [65]. Another approach to solve the 1D models is to linearize the system by neglecting the convection term and then find solutions in frequency domain [66,67].

The method of characteristics could provide a solution of the system of PDEs (continuity and momentum) transforming them into ordinary differential equations (ODEs) along the directions of the characteristic lines [67-71]. The governing equations have also been solved using finite difference methods such as the Lax-Wendroff and MacCormack schemes [72-76]. In recent years, various finite difference [9,10,63,72,76-78], finite volume [79,80], finite element [58,81-84], discontinuous Galerkin schemes [81,83,85-87], or combination of the above numerical methods [88] have been applied on this problem. The Godunov scheme was used to discretise the governing equations in a finite volume formulation [89,90]. For the finite element formulation, Formaggia, et al. adopted the Yoshida projection scheme for the solution of the equations [91]. Wan, et al. used a discontinuous Galerkin scheme [92]. Porenta, et al. [93] and Rooz, et al. [94] applied a Galerkin scheme and Sherwin, et al. solved the equations both with a discontinuous Galerkin scheme and with a Taylor-Galerkin scheme [95]. Wan, et al. [64] and Steele, et al. [96] have described a method to solve the 1D nonlinear equations of blood flow in elastic vessels utilizing a space-time finite element method with Galerkin/Least-Squares (GLS) stabilization technique. Numerical schemes have also been designed to solve the nonlinear equations in time domain [50,97]. Another class of models are described by power law [98] and more recently, models with viscous boundary layers have been proposed [9,99-101].

A small number of researchers have used spectral method for the solution of pulse wave equations. Bessems, et al. have applied a Galerkin weighted residual method to transform the governing equations into a spectral element space [100]. Sherwin, et al. applied the spectral/hp element method [102]. Ballarin and colleagues have developed a parameterized approach of the Navier-Stokes equations utilizing the POD-Galerkin approximation [103]. Additional studies used spectral method to perform 1D flow simulations [104,105]. Several researchers have proposed stochastic approaches for the human arterial network hemodynamics or for the boundary conditions of the developed model [106-109].

An effective way to describe the arterial structure that consists of thousands to millions of arteries is by using the concept of fractal tree models. Perdikaris, et al. have developed a flexible and effective model that accurately distributes flow in the downstream vasculature and can stably provide a physiological pressure outflow boundary condition [110]. They have scaled up a Discontinuous Galerkin solver that utilizes the MPI/Open MP hybrid programming to thousands of computer cores simulating blood flow in networks of millions of arterial segments. Linninger, et al. developed a computer fractal-like tree model that involves arterial, capillary and venous blood vessels of the cerebral microvascular bed as well as brain tissue occupying extra vascular space [111].

Finally, there is a small number of researchers [112,113] who specifically included the inertial forces in their 1D model derivation, and arrived at a wave dynamics equation in the form of the Korteweg-de Vries (KdV) equation. The corresponding wave dynamics is governed by a special kind of wave called solitary wave. The solitary wave is a better description of the arterial pulse wave since it matches the experimental results better than the hyperbolic wave equation that is currently used by the majority of researchers. This seems to be an interesting area that requires further exploration [112-116].

Boundary conditions

Due to the hyperbolic nature of the 1D pulse wave equation, boundary condition (BC) has to be imposed to each end of the vessel [57]. At the inlet of the vessel, the pressure or flow rate can be applied based on derivations or experimental data. For the outlet side, the boundary condition requires more consideration. Many researchers have directly specified a combination of the pressure and flow rate at the inlet and outlet. Other researchers used constant or varying resistance or a three-element Windkessel to specify the pressure/flow relation at the outlet [64,67,74,75,93,94]. Others have chosen to specify the wave reflection coefficient at the outlet [78,83,88] or used the non-reflecting boundary condition and compatibility condition [117].

The most popular downstream conditions in recent studies are to use a Windkessel model as an after-load or directly to specify the wave reflection coefficient. Olufsen proposed the structured tree model in which the impedance of smaller arterioles was estimated with linearised Navier-Stokes equations further improving the accuracy of downstream boundary condition [62]. Smith, et al. studied the blood flow in coronary network, and a pressure dependent vessel network for the coronary arteriole, capillary and venules was used as terminal load to each generation of coronary artery branches [76]. A special kind of boundary condition internal to a vessel segment is that of vessel branching, in which a parent vessel is branched into several daughter vessels [9,10,118]. Many researchers directly applied equal static pressures and conservation of flow rates at the branching points [62,64,93]. Sherwin, et al. proposed an improved description applying continuity of total pressure [95]. Recently, Morbiducci, et al. proposed inflow boundary conditions for image-based computational hemodynamics [119]. They study the impact of idealized versus measured velocity profiles in the human aorta and concluded that idealized velocity profiles as inlet BCs can lead to misleading representations of the aortic hemodynamics both in terms of disturbed shear and bulk flow structures.

Problems of 1D models

There are several complications in the study of 1D pulse wave propagation, including the tapering of the vessel branching, nonlinear pressure/cross-sectional area relationships for the vessel wall, axial tension and bending in the vessel wall, collapse of veins and pulmonary vessels. In deriving the governing equations, most researchers have considered the nonlinear pressure/cross-sectional area relation of the vessel wall by incorporating individually adapted constitutive relations. An additional factor that influences the validity of 1D models is the blood rheology as the Newtonian approach seems to be restrictive when looking for an accurate estimation of wall shear stress [120]. In vessels with an internal diameter of less than 1mm, the apparent viscosity is dependent significantly on temperature and shear rate [18]. However, in vessels smaller than this value, we can change the friction coefficient to account the altered viscosity. Researchers have developed non-Newtonian models, such as the Casson viscoplastic model, to describe arterial blood flow [121]. Another approach is the Dissipative Particle Dynamics (DPD) in combination with 1D global models of blood circulation [122]. Since blood is considered as a heterogeneous fluid composed of plasma and blood cells, DPD is a novel multi-scale approach to describe blood dynamics.

Lateral leakage and tapering can be modeled by the 1D models. The aorta is tapering from the proximal to the distal end. The tapering wall increases the pulse pressure by continuous reflection. It is also observed that there are tiny side branches at the aorta. Some studies show that the effect of tapering wall is compensated by the blood loss to the side branches. In net effect, it is more like a flow in a straight tube with no lateral leakage [18]. Brook and Pedley [90], Porenta, et al. [93], Formaggia, et al. [91], Rooz, et al. [94], Sherwin, et al. [95,102] included the effect of vessel tapering by considering a varying initial cross-sectional area of the vessel.

Since the mean Reynolds number could take a value of 4000 during the cardiac cycle [123], the flow should be described as turbulent. In unsteady case the flow is at least transitional to turbulence. In small arteries, the Reynolds number drops substantially due to the fact that the velocity and the diameter of the vessels become smaller. Given that the Womersley number is also much smaller in small arteries, laminar flow is likely to appear in small arteries. That gives justification to Poiseuille theory in estimating the peripheral resistance. In medium-sized arteries, there may be transition conditions between turbulent and laminar flow. The 1D models neglect the velocity components in the circumferential direction and thus a laminar flow is an implicit assumption. In the aorta, the wave speed is about 5 m/s and the radius is about 10 mm [18]. If we assume the period of one pulse is 1s, the ratio between the wave length and the radius is 500. In smaller arteries, the wave speed increases and the radius decreases, the ratio becomes even bigger. Thus the long wave assumption is fully justified. One crucial step in deriving the 1D model is to prescribe a proper axial velocity profile. The fluid friction coefficient and the correction factor of the convection term in the momentum balance equation are dependent on this profile.

In clinical applications, the blood pressure is measured when the subject is in supine or sitting position. In those cases, the pressure difference through the whole body caused by gravity is much smaller than the pressure at the arterial system. Curvature and bifurcation will dissipate blood flow energy; an experimental study shows that the energy loss at bifurcations is very small [81]. Since the network of vessels is very large, we usually have to truncate it at some levels. The truncated sub-networks have to be described properly. Reflection coefficient, structured tree [9], 0D models [124] and other kind of generalized methods for specific numerical schemes [58] could lead to problems in 1D cardiovascular models.

With some modifications, the 1D models can be used in simulation of venous flow. There are three special features of venous system that need to be treated, the inflow from venules bed, muscular contraction and valves. The inflow can be considered as a source term in the mass conservation equation, the muscular contraction can be described by an external pressure in the constitutive equation of the vessel wall; the valves, which in fact allow very small reverse flows, can be modeled by very large resistances when blood's pressure gradient to the heart is adverse [125].

The constitutive equation of the wall is mainly derived from thin shell theory. The wall shows nonlinear elasticity properties in high pressure and the inertia of the wall may affect the pulse wave as well. Usually linear elastic models are integrated into the 1D fluid models for simplicity. Recent studies indicate that the viscoelasticity may have significant influence on the pulse waves [63,81,100,126-130].

Applications of 1D models

Several 1D models of the vessel network have been proposed for the study of pulse wave transmission in various applications [62,64,67-71,73,75,89-91,93-95,131]. The models mainly differ in the boundary conditions applied and the solution methods used, and whether nonlinear effects were taken into account.

Stergiopulos and collaborators solved the nonlinear 1D blood flow equations in a comprehensive model of the arterial system using a lumped parameter model of the vasculature downstream of each branch to account for the capacitive and resistive vasculature effects [63]. Earlier work had been done on modeling flow in a single tapering tube where the 1D nonlinear equations were coupled to Windkessel models [132,133]. Although the geometry was simple, these studies conveyed most of the ideas such as the effect of nonlinearity, tapering, stenosis and dilatation of the distal beds on pressure and flow waveforms. Wang, et al. studied the coupling of the 1D linear equations with terminal resistances using simplified input data [67]. Sherwin, et al. compared the 1D linear model to the equivalent non-linear one [95,102]. Several groups have mathematically analyzed and developed the coupling of 1D non-linear equations with lumped models [124,134,135].

In contrast to methods coupling the 1D equations of blood flow to lumped parameter models, Olufsen, et al. developed a distributed model based on calculating the input impedance of an asymmetric binary structured tree using Womersley's linear wave theory [60] and an algorithm for computing the impedance of a vascular network initially proposed by Taylor [136]. Olufsen's distributed model of the downstream vasculature enabled the representation of more realistic flow and pressure waveforms than those obtained with lumped parameter models [62]. Steele, et al. used a modified version of Olufsen's impedance boundary condition to model blood flow at rest and during simulated exercise conditions [96]. In this case, vascular networks were assigned to the outlets of a model of the abdominal aorta, modified to represent the resting flow distribution of eleven different subjects and then dilated to simulate the effects of lower limb exercise.

Overall, the 1D models are well balanced between complexity and computation cost, thus they are very suitable for many biomedical applications [127,137]. Most of the 1D pulse wave transmission models have been applied to study the pulse wave dynamics in arterial segments [68-70]. Wang, et al. [71], and Wang and Parker [67] later extended the study to investigate the pulse wave dynamics in a complete arterial network, including ventricular-arterial coupling. Li and Cheng [73] studied the pulse wave features in the pulmonary arterial network. A model of the human cardiovascular-respiratory control system with one and two transport delays in the state equations describing the respiratory system was developed by Kappel, et al. [138,139]. The model can be used to study the interaction between cardiovascular and respiratory function in various situations as well as to consider the influence of optimal function in physiological control system performance. The model was applied to the simulation of the orthostatic stress phenomenon [140-142], which was also considered by Olufsen, et al. [143].

In one class of 1D model applications, we simulate the diseased blood flow in various surgery plans hoping that optimized guidance to surgeons may be given successfully. Even though there are many difficulties on setting the parameters of patient-specific models and usually only qualitatively accurate predictions can be given, we still can extract clinically relevant information. Huberts, et al. show that the mean pressures and flows after an arteriovenous fistula surgery can be simulated with 1D models with satisfactory accuracy [144]. Another successful example is the simulation of blood flow after bypass surgery [145]. Porenta, et al. [93] and Rooz, et al. [94] have studied the pulse wave features in arteries with stenosis. Wan, et al. [64] and Steele, et al. [92] calculated the pulse wave dynamics in diseased arterial vessels with bypass grafts. Surovtsova [131], Sherwin, et al. [95], and Pontrelli and Rossoni [74] studied the pulse wave transmission in stenotic arteries with implanted stents. Formaggia, et al. studied wave propagation and reflection due to stenting, solving the 1D nonlinear equations of blood flow with a prescribed pressure at the inlet and a non-reflecting outlet boundary condition representing a tube of infinite length [146]. They proposed an approach for the coupling with myocardial contraction [147,148].

Another development in 1D pulse wave transmission modeling is the wave intensity analysis proposed by Parker and Jones [69], in which they defined the product of pressure and velocity changes over a small interval as the evaluation of rate of energy flux per unit area in a profile of vessel segment. This indicator accurately describes the wave intensity accompanying the pulse wave transmission, and can be used to distinguish the forward transmission wave from the backward one. The wave intensity analysis has been applied for the study of pulse wave transmission in the left ventricle [149,150], coronary vessels [151], systemic arteries [152] and pulmonary arteries [153]. Some researchers have studied the pulse wave transmission in collapsible vessels. Elad, et al. studied the unsteady fluid flow through collapsible tubes [72].

The most advanced 1D cardiovascular models are taking under consideration the coupling of the blood with the arterial or venous wall. The properties of the vascular wall, elastic or viscoelastic, are governed by the wall equilibrium equations. Most researchers use simple linear or nonlinear constitutive equations to describe the pressure/cross-sectional area relationship [62,64,67-73,75,76,89-91,93-95,102,131]. However, more complex models are also available [74]. Pontrelli and colleagues studied the modeling of the wall using the coupling of simple lumped models with a six-compartment lumped model, representing the whole system as a closed loop [154,155].

Multi-scale models

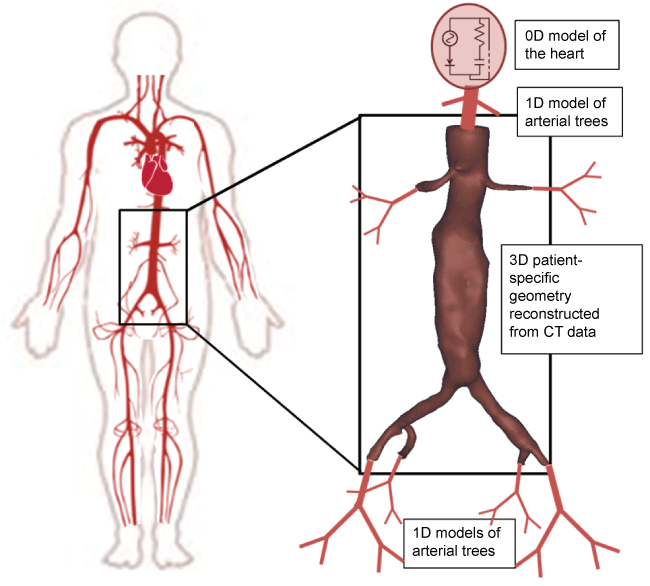
Low-dimensional models (0D and 1D) are suitable for the characterization of blood flow along extended parts of the cardiovascular systems but, due to their design, fail to account for the complexity of the local vascular geometry. Multi-scale models for cardiovascular hemodynamics have been recently developed to combine the efficiency of the continuum models with the higher fidelity of the atomistic or mesoscopic models leading to hybrid type computations [156-159]. A representation of a multi-scale cardiovascular model is shown in figure 2.

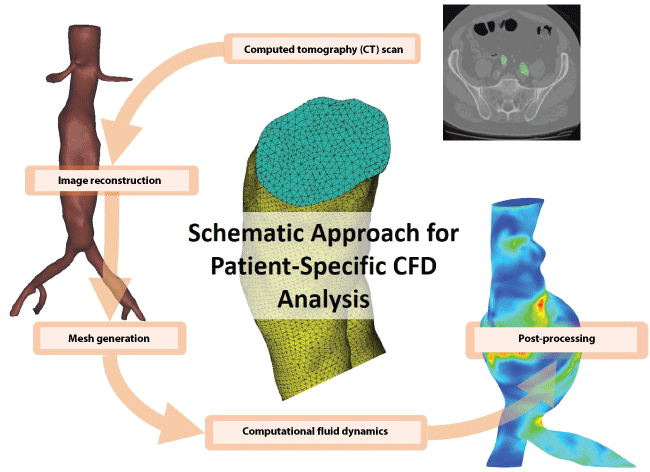
Higher dimensional models (2D and 3D) are able to predict the hemodynamic properties in more detail as they can account for the local vascular geometry, especially the patient-specific 3D models that derive from reconstructions of medical screening data, according to the workflow of figure 3. However, due to the intense computational requirements, the 3D models are normally restricted to smaller arterial segments [160]. Additionally, the predictability of 3D models largely depends on the accurate description of the boundary conditions. It is apparent therefore that the utilization of 3D models does not guarantee the accurate simulation of the in vivo blood flow conditions. The limitations of the various models are neutralized when combined in unified studies where low-dimensional models are attached at the inlets and outlets of the 3D computational domains [161]. Every sub-model lends different characteristics to the unified model as it is governed by different type of equations. The 0D lumped parameter models are governed by ODEs, the 1D models are mostly described by hyperbolic PDEs, while the 2D/3D models are based on the Navier-Stokes equations [45].

Methods to couple higher and lower dimensional models were initially outlined by Formaggia, et al. where the proposed iterative coupling was tested initially in simplified computational domains [91]. Pant, et al. introduced a framework for the estimation of lumped parameters based on sensitivity analysis tools and the sequential estimation approach of the unscented Kalman filter aiming to increase the levels of patient-specific analysis of hemodynamic flow [162]. Kim, et al. demonstrated the coupling of a lumped parameter heart model to a 3D finite element model of the aorta [2]. Extending the applicability of the coupling, Chandra, et al. applied boundary conditions that capture the wave propagation, in 3D fluid-structure interaction models of arterial blood flow [163]. Smith, et al. generated an anatomically-based coronary geometrical model [147], and then performed 1D simulations on six generations of vessels, using physiologically relevant lumped boundary conditions [76].

Validation

At the beginning, low-dimensional models agreed quantitatively with experimental observations when accurate parameters of the models were available [78,81]. In several cases the numerical results only meet qualitatively with in vivo data [9,75,92,164-166]. To know the sensitivity of the output to the uncertainties of each parameter of the 1D models, sensitivity analysis has been done [11,49,167]. To estimate the parameters, we can compare the model output with measurements and minimize the difference by tuning the parameters [116,168]. Many applications of the 1D models rely on the solution of the reverse problems. However, in these studies, the computations have to run millions of times, which contribute to the development of a fast numerical code.

From the above analysis is imperative to highlight that all these studies have to be validated against experimental measurements. Researchers have done substantial effort to validate the low-dimensional approaches [92,106,144,145,169]. Reymond, et al. extended and improved a previous 1D model of the systemic circulation by including a heart model, a detailed description of the cerebral arterial tree, viscoelasticity, and a Witzig-Womersley theory-based formulation for the friction and convective acceleration terms [75]. Morbiducci, et al. developed inflow boundary conditions for image-based computational hemodynamics. Their findings indicate that assumptions upon the shape of the inlet velocity profile in subject-specific in silico studies of the aortic hemodynamics might have completely different impact on the aortic bulk flow topology and on disturbed shear [119]. They also developed a model for atherosclerosis at arterial bifurcations. Arterial bifurcations can be exposed to disturbed shear stress and there by affected by local plaque formation, which reflects a complex interplay among hemodynamics, biological and systemic risk factors [170]. Van der Horst, et al. presented two disease types models, coronary stenoses located in the epicardial vessels and left ventricular hypertrophy with an aortic valve stenosis, affecting the coronary microvasculature [171]. Guala, et al. presented a detailed subject-specific validation against in vivo measurements from a population of six healthy young men. Several quantities of heart dynamics such as the mean ejected flow, ejection fraction, and left-ventricular end-diastolic, end-systolic and stroke volumes and the pressure waveforms are compared with measured data [172].

Conclusions

The purpose of this review is to discuss recent advances and evolution of low-dimensional models of human cardiovascular system and its applications. Configurations of the 0D models are becoming more sophisticated and advanced, and the various developed models have wide and successful applications in the study of cardiovascular physiology, evaluation of new devices and more. The 1D models were mainly confined to the study of arterial hemodynamics, where their ability to capture wave propagation effects is imperative, with minor extensions to venous dynamics. These models have been successfully applied in the context of clinical diagnosis of pathological changes in the cardiovascular system, such as hypertension, atherosclerosis, and in stent design. With the development of computers and numerical analysis techniques, higher dimensional hemodynamic analysis (2D/3D) using computational fluid dynamics is no longer prohibitive. So, in order to obtain very accurate results and to simulate the interaction among cardiovascular organs, it is required to couple the 0D models and the 1D/2D/3D models to build multi-dimensional and multi-scale models. It is possible in the near future to have accurate, real-time, patient-specific, clinically applicable cardiovascular models for the simulation of the whole human body cardiovascular dynamics.

References

1. Levick JR (2013) An introduction to cardiovascular physiology. Butterworth-Heinemann.
   


2. Kim HJ, Figueroa CA, Hughes TJR, Jansen KE, Taylor CA (2009) Augmented lagrangian method for constraining the shape of velocity profiles at outlet boundaries for three-dimensional finite element simulations of blood flow.Computer Methods in Applied Mechanics and Engineering 198: 3551-3566.
   


3. Van de Vosse F, De Hart J, Van Oijen C, Bessems D, Gunther T, et al. (2003) Finite-element-based computational methods for cardiovascular fluid-structure interaction. Journal of Engineering Mathematics 47: 335-368.
   


4. Avolio A (1992) Ageing and wave reflection. J Hypertens Suppl 10: S83-86.
   


5. Barnard AC, Hunt WA, Timlake WP, Varley E (1966) A theory of fluid flow in compliant tubes. Biophys J 6: 717-724.
   


6. Bassingthwaighte JB, Liebovitch LS, West BJ (2013) Fractal physiology. Springer.
   


7. Caro CG, Pedley TJ, Schroter RC, Seed WA (1978) The mechanics of the circulation. Journal of Fluid Mechanics Oxford University Press.
   


8. Chorin AJ, Marsden JE (1990) A mathematical introduction to fluid mechanics. Springer, New York
   


9. Olufsen MS, Peskin CS, Kim WY, Pedersen EM, Nadim A, et al. (2000) Numerical simulation and experimental validation of blood flow in arteries with structured-tree outflow conditions. Annals of Biomedical Engineering 28: 1281-1299.
   


10. Zagzoule M, Marc-Vergnes JP (1986) A global mathematical model of the cerebral circulation in man. J Biomech 19: 1015-1022.
    


11. Leguy CAD, Bosboom EM, Belloum AS, Hoeks AP, van de Vosse FN (2011) Global sensitivity analysis of a wave propagation model for arm arteries. Med Eng Phys 33: 1008-1016.
    


12. Berger DS, Li JK (1992) Temporal relation between left ventricular and arterial system elastances. IEEE Trans Biomed Eng 39: 404-410.
    


13. Cavalcanti S, Belardinelli E (1996) Modeling of cardiovascular variability using a differential delay equation. IEEE Trans Biomed Eng 43: 982-989.
    


14. Diaz-Zuccarini V, LeFevre J (2007) An energetically coherent lumped parameter model of the left ventricle specially developed for educational purposes. Computers in Biology and Medicine 37: 774-784.
    


15. Drzewiecki G, Wang JJ, Li JKJ, Kedem J, Weiss H (1996) Modeling of mechanical dysfunction in regional stunned myocardium of the left ventricle. IEEE Trans Biomed Eng 43: 1151-1163.
    


16. Green JF, Miller NC (1973) A model describing the response of the circulatory system to acceleration stress. Ann Biomed Eng 1: 455-467.
    


17. Li JKJ (2000) The arterial circulation: Physical principles and clinical applications. Springer Science & Business Media.
    


18. Nichols W, O'Rourke M, Vlachopoulos C (2011) Mcdonald's blood flow in arteries: Theoretical, experimental and clinical principles. CRC Press.
    


19. Westerhof N, Bosman F, De Vries CJ, Noordergraaf A (1969) Analog studies of the human systemic arterial tree. J Biomech 2: 121-143.
    


20. Beyar R, Hausknecht MJ, Halperin HR, Yin FCP, Weisfeldt ML (1987) Interaction between cardiac chambers and thoracic pressure in intact circulation. Am J Physiol 253: H1240-H1252.
    


21. Burkhoff D, Tyberg JV (1993) Why does pulmonary venous-pressure rise after onset of LV dysfunction: A theoretical analysis. Am J Physiol 265: H1819-H1828.
    


22. Santamore WP, Burkhoff D (1991) Hemodynamic consequences of ventricular interaction as assessed by model analysis. Am J Physiol 260: H146-H157.
    


23. Ursino M (1999) A mathematical model of the carotid baroregulation in pulsating conditions. IEEE Trans Biomed Eng 46: 382-392.
    


24. Ursino M, Fiorenzi A, Belardinelli E (1996) The role of pressure pulsatility in the carotid baroreflex control: A computer simulation study. Comput Biol Med 26: 297-314.
    


25. Zácek M, Krause E (1996) Numerical simulation of the blood flow in the human cardiovascular system. J Biomech 29: 13-20.
    


26. Beyar R, Dong SJ, Smith ER, Belenkie I, Tyberg JV (1993) Ventricular interaction and septal deformation: a model compared with experimental data. Am J Physiol 265: H2044-2056.
    


27. Chung DC, Niranjan SC, Clark JW, Bidani A, Johnston WE, et al. (1997) A dynamic model of ventricular interaction and pericardial influence. Am J Physiol 272: H2942-H2962.
    


28. Korakianitis T, Shi YB (2006) A concentrated parameter model for the human cardiovascular system including heart valve dynamics and atrioventricular interaction. Med Eng Phys 28: 613-628.
    


29. Korakianitis T, Shi YB (2006) Effects of atrial contraction, atrioventricular interaction and heart valve dynamics on human cardiovascular system response. Med Eng Phys 28: 762-779.
    


30. Olansen JB, Clark JW, Khoury D, Ghorbel F, Bidani A (2000) A closed-loop model of the canine cardiovascular system that includes ventricular interaction. Computers and Biomedical Research 33: 260-295.
    


31. Santamore WP, Shaffer T, Papa L (1990) Theoretical model of ventricular interdependence pericardial effects. Am J Physiol 259: H181-H189.
    


32. Sun Y, Beshara M, Lucariello RJ, Chiaramida SA (1997) A comprehensive model for right-left heart interaction under the influence of pericardium and baroreflex. Am J Physiol 272: H1499-H1515.
    


33. Slinker BK, Chagas ACP, Glantz SA (1987) Chronic pressure overload hypertrophy decreases direct ventricular interaction. Am J Physiol 253: H347-H357.
    


34. Burattini R, Natalucci S (1998) Complex and frequency-dependent compliance of viscoelastic windkessel resolves contradictions in elastic windkessels. Med Eng Phys 20: 502-514.
    


35. Bovendeerd PHM, Borsje P, Arts T, van De Vosse FN (2006) Dependence of intramyocardial pressure and coronary flow on ventricular loading and contractility: a model study. Ann Biomed Eng 34: 1833-1845.
    


36. Geven MCF, Bohte VN, Aarnoudse WH, van den Berg PMJ, Rutten MCM, et al. (2004) A physiologically representative in vitro model of the coronary circulation. Physiol Meas 25: 891-904.
    


37. Manor D, Beyar R, Sideman S (1994) Pressure-flow characteristics of the coronary collaterals: a model study. Am J Physiol 266: H310-318.
    


38. Pennati G, Bellotti M, Fumero R (1997) Mathematical modelling of the human foetal cardiovascular system based on doppler ultrasound data. Med Eng Phys 19: 327-335.
    


39. Snyder MF, Rideout VC (1969) Computer simulation studies of the venous circulation. IEEE Trans Biomed Eng 16: 325-334.
    


40. Ursino M (1991) A mathematical model of overall cerebral blood flow regulation in the rat. IEEE Trans Biomed Eng 38: 795-807.
    


41. Ursino M, Giulioni M (2003) Quantitative assessment of cerebral autoregulation from transcranial doppler pulsatility: A computer simulation study. Med Eng Phys 25: 655-666.
    


42. Ursino M, Iezzi M, Stocchetti N (1995) Intracranial pressure dynamics in patients with acute brain-damage: A critical analysis with the aid of a mathematical model. IEEE Trans Biomed Eng 42: 529-540.
    


43. Ursino M, Ter Minassian A, Lodi CA, Beydon L (2000) Cerebral hemodynamics during arterial and CO2 pressure changes: In vivo prediction by a mathematical model. Am J Physiol 279: H2439-H2455.
    


44. Milisic V, Quarteroni A (2004) Analysis of lumped parameter models for blood flow simulations and their relation with 1D models. ESAIM-Mathematical Modelling and Numerical Analysis 38: 613-632.
    


45. Quarteroni A, Veneziani A, Vergara C (2016) Geometric multiscale modeling of the cardiovascular system, between theory and practice. Computer Methods in Applied Mechanics and Engineering 302: 193-252.
    


46. Shi Y, Lawford P, Hose R (2011) Review of zero-D and 1-D models of blood flow in the cardiovascular system. Biomed Eng Online 10: 33.
    


47. Slinker BK, Glantz SA (1986) End-systolic and end-diastolic ventricular interaction. Am J Physiol 251: H1062-1075.
    


48. Quarteroni A, Lassila T, Rossia S, Ruiz-Baiera R (2016) Integrated heart-coupling multiscale and multiphysics models for the simulation of the cardiac function. Computer Methods in Applied Mechanics and Engineering.
    


49. Ryu J, Hu X, Shadden SC (2015) A coupled lumped-parameter and distributed network model for cerebral pulse-wave hemodynamics. J Biomech Eng 137: 101009.
    


50. Ferranti F, Tamburrelli V, Antonini G (2015) Rational macromodeling of 1D blood flow in the human cardiovascular system. Int J Numer Method Biomed Eng 31.
    


51. Hall JE (2006) Guyton and hall: Textbook of medical physiology. Elsevier, Philadelphia.
    


52. Cornelissen AJM, Dankelman J, VanBavel E, Spaan JAE (2002) Balance between myogenic, flow-dependent, and metabolic flow control in coronary arterial tree: A model study. Am J Physiol Heart Circ Physiol 282: H2224-H2237.
    


53. Cornelissen AJM, Dankelman J, VanBavel E, Stassen HG, Spaan JAE (2000) Myogenic reactivity and resistance distribution in the coronary arterial tree: A model study. Am J Physiol Heart Circ Physiol 278: H1490-H1499.
    


54. Jeays AD, Lawford PV, Gillott R, Spencer PA, Bardhan KD, et al. (2007) A framework for the modeling of gut blood flow regulation and postprandial hyperaemia. World J Gastroenterol 13: 1393-1398.
    


55. Lodi CA, Ursino M (1999) Hemodynamic effect of cerebral vasospasm in humans: a modeling study. Ann Biomed Eng 27: 257-273.
    


56. Kappel F, Peer RO (1993) A mathematical model for fundamental regulation processes in the cardiovascular system. J Math Biol 31: 611-631.
    


57. Fung YC (1984) Biodynamics: Circulation. Springer Science, Business Media.
    


58. Vignon IE, Taylor CA (2004) Outflow boundary conditions for one-dimensional finite element modeling of blood flow and pressure waves in arteries. Wave Motion 39: 361-374.
    


59. Whitham GB (1999) Linear and nonlinear waves. Wiley, New York.
    


60. Womersley JR (1955) Oscillatory motion of a viscous liquid in a thin-walled elastic tube: The linear approximation for long waves. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science 46: 199-221.
    


61. Avolio AP (1980) Multi-branched model of the human arterial system. Medical & Biological Engineering & Computing 18: 709-718.
    


62. Olufsen MS (1999) Structured tree outflow condition for blood flow in larger systemic arteries. Am J Physiol 276: H257-H268.
    


63. Stergiopulos N, Young DF, Rogge TR (1992) Computer simulation of arterial flow with applications to arterial and aortic stenoses. J Biomech 25: 1477-1488.
    


64. Wan J, Steele B, Spicer SA, Strohband S, Feijoo GR, et al. (2002) A one-dimensional finite element method for simulation-based medical planning for cardiovascular disease. Comput Methods Biomech Biomed Engin 5: 195-206.
    


65. Huang PG, Muller LO (2015) Simulation of one-dimensional blood flow in networks of human vessels using a novel TVD scheme. International Journal for Numerical Methods in Biomedical Engineering 31.
    


66. Nicoud F, Vernhet H, Dauzat M (2005) A numerical assessment of wall shear stress changes after endovascular stenting. J Biomech 38: 2019-2027.
    


67. Wang JJ, Parker KH (2004) Wave propagation in a model of the arterial circulation. J Biomech 37: 457-470.
    


68. Bodley WE (1971) The non-linearities of arterial blood flow. Phys Med Biol 16: 663-672.
    


69. Parker KH, Jones CJH (1990) Forward and backward running waves in the arteries: Analysis using the method of characteristics. J Biomech Eng 112: 322-326.
    


70. Streeter VL, Keitzer Wf, Bohr Df (1963) Pulsatile Pressure And Flow Through Distensible Vessels. Circ Res 13: 3-20.
    


71. Wang JJ, O'Brien AB, Shrive NG, Parker KH, Tyberg JV (2003) Time-domain representation of ventricular-arterial coupling as a windkessel and wave system. Am J Physiol Heart Circ Physiol 284: H1358-H1368.
    


72. Elad D, Katz D, Kimmel E, Einav S (1991) Numerical schemes for unsteady fluid flow through collapsible tubes. J Biomed Eng 13: 10-18.
    


73. Li CW, Cheng HD (1993) A nonlinear fluid model for pulmonary blood circulation. J Biomech 26: 653-664.
    


74. Pontrelli G, Rossoni E (2003) Numerical modelling of the pressure wave propagation in the arterial flow. International Journal for Numerical Methods in Fluids 43: 651-671.
    


75. Reymond P, Merenda F, Perren F, Rüfenacht D, Stergiopulos N (2009) Validation of a one-dimensional model of the systemic arterial tree. Am J Physiol Heart Circ Physiol 297: H208-222.
    


76. Smith NP, Pullan AJ, Hunter PJ (2002) An anatomically based model of transient coronary blood flow in the heart. SIAM Journal on Applied Mathematics 62: 990-1018.
    


77. Kroon W, Huberts W, Bosboom M, van de Vosse F (2012) A numerical method of reduced complexity for simulating vascular hemodynamics using coupled 0D lumped and 1D wave propagation models. Comput Math Methods Med 2012: 156094.
    


78. Saito M, Ikenaga Y, Matsukawa M, Watanabe Y, Asada T, et al. (2011) One-dimensional model for propagation of a pressure wave in a model of the human arterial network: Comparison of theoretical and experimental results. J Biomech Eng 133.
    


79. Cavallini N, Caleffi V, Coscia V (2008) Finite volume and weno scheme in one-dimensional vascular system modelling. Computers & Mathematics with Applications 56: 2382-2397.
    


80. Delestre O, Lagree PY (2013) A 'well-balanced' finite volume scheme for blood flow simulation. International Journal for Numerical Methods in Fluids 72: 177-205.
    


81. Alastruey J, Khir AW, Matthys KS, Segers P, Sherwin SJ, et al. (2011) Pulse wave propagation in a model human arterial network: Assessment of 1-D visco-elastic simulations against in vitro measurements. J Biomech 44: 2250-2258.
    


82. Formaggia L, Lamponi D, Quarteroni A (2003) One-dimensional models for blood flow in arteries. Journal of Engineering Mathematics 47: 251-276.
    


83. Guadagni G, Bove EL, Migliavacca F, Dubini G (2001) Effects of pulmonary afterload on the hemodynamics after the hemi-Fontan procedure. Med Eng Phys 23: 293-298.
    


84. Malossi ACI, Blanco PJ, Deparis S (2012) A two-level time step technique for the partitioned solution of one-dimensional arterial networks. Computer Methods in Applied Mechanics and Engineering 237: 212-226.
    


85. LaDisa JF, Olson LE, Guler I, Hettrick DA, Kersten JR, et al. (2005) Circumferential vascular deformation after stent implantation alters wall shear stress evaluated with time-dependent 3D computational fluid dynamics models. J Appl Physiol (1985) 98: 947-957.
    


86. Matthys KS, Alastruey J, Peiro J, Khir AW, Segers P, et al. (2007) Pulse wave propagation in a model human arterial network: Assessment of 1-D numerical simulations against in vitro measurements. J Biomech 40: 3476-3486.
    


87. Mynard JP, Nithiarasu P (2008) A 1D arterial blood flow model incorporating ventricular pressure, aortic valve and regional coronary flow using the locally conservative galerkin (LCG) method. Communications in Numerical Methods in Engineering 24: 367-417.
    


88. Wang X, Fullana JM, Lagree PY (2015) Verification and comparison of four numerical schemes for a 1D viscoelastic blood flow model. Computer Methods in Biomechanics and Biomedical Engineering 18: 1704-1725.
    


89. Brook BS, Falle SAEG, Pedley TJ (1999) Numerical solutions for unsteady gravity-driven flows in collapsible tubes: Evolution and roll-wave instability of a steady state. Journal of Fluid Mechanics 396: 223-256.
    


90. Brook BS, Pedley TJ (2002) A model for time-dependent flow in (giraffe jugular) veins: uniform tube properties. J Biomech 35: 95-107.
    


91. Formaggia L, Gerbeau JF, Nobile F, Quarteroni A (2001) On the coupling of 3D and 1D Navier-Stokes equations for flow problems in compliant vessels. Computer Methods in Applied Mechanics and Engineering 191: 561-582.
    


92. Steele BN, Wan J, Ku JP, Hughes TJ, Taylor CA (2003) In vivo validation of a one-dimensional finite-element method for predicting blood flow in cardiovascular bypass grafts. IEEE Trans Biomed Eng 50: 649-656.
    


93. Porenta G, Young DF, Rogge TR (1986) A finite-element model of blood flow in arteries including taper, branches, and obstructions. J Biomech Eng 108: 161-167.
    


94. Rooz E, Young DF, Rogge TR (1982) A finite-element simulation of pulsatile flow in flexible obstructed tubes. J Biomech Eng 104: 119-124.
    


95. Sherwin SJ, Formaggia L, Peiro J, Franke V (2003) Computational modelling of 1D blood flow with variable mechanical properties and its application to the simulation of wave propagation in the human arterial system. International Journal for Numerical Methods in Fluids 43: 673-700.
    


96. Steele BN, Olufsen MS, Taylor CA (2007) Fractal network model for simulating abdominal and lower extremity blood flow during resting and exercise conditions. Comput Methods Biomech Biomed Engin 10: 39-51.
    


97. Guan D, Liang F, Gremaud PA (2016) Comparison of the windkessel model and structured-tree model applied to prescribe outflow boundary conditions for a one-dimensional arterial tree model. Journal of Biomechanics 49: 1583-1592.
    


98. Hughes JR, Lubliner J (1973) On the one-dimensional theory of blood flow in the larger vessels. Mathematical Biosciences 18: 161-170.
    


99. Azer K, Peskin CS (2007) A one-dimensional model of blood flow in arteries with friction and convection based on the Womersley velocity profile. Cardiovasc Eng 7: 51-73.
    


100. Bessems D, Giannopapa CG, Rutten MCM, van de Vosse FN (2008) Experimental validation of a time-domain-based wave propagation model of blood flow in viscoelastic vessels. J Biomech 41: 284-291.
     


101. Lagree PY (2000) An inverse technique to deduce the elasticity of a large artery. Eur Phys J AP 9: 153-163.
     


102. Sherwin SJ, Franke V, Peiro J, Parker K (2003) One-dimensional modelling of a vascular network in space-time variables. Journal of Engineering Mathematics 47: 217-250.
     


103. Ballarin F, Manzoni A, Quarteroni A, Rozza G (2015) Supremizer stabilization of POD-galerkin approximation of parametrized steady incompressible Navier-Stokes equations. International Journal for Numerical Methods in Engineering 102: 1136-1161.
     


104. Acosta S, Puelz C, Riviére B, Penny DJ, Rusin CG (2015) Numerical Method of Characteristics for One-Dimensional Blood Flow. J Comput Phys 294: 96-109.
     


105. Tamburrelli V, Ferranti F, Antonini G, Cristina S, Dhaene T, et al. (2010) Spectral models for 1D blood flow simulations. Conf Proc IEEE Eng Med Biol Soc 2010.
     


106. Brault A, Dumas L, Lucor D (2016) Uncertainty quantification of inflow boundary condition and proximal arterial stiffness coupled effect on pulse wave propagation in a vascular network. arXiv preprint.
     


107. Chen P, Quarteroni A, Rozza G (2013) Simulation-based uncertainty quantification of human arterial network hemodynamics. Int J Numer Method Biomed Eng 29: 698-721.
     


108. Eck VG, Feinberg J, Langtangen HP, Hellevik LR (2015) Stochastic sensitivity analysis for timing and amplitude of pressure waves in the arterial system. International Journal for Numerical Methods in Biomedical Engineering 31.
     


109. Sankaran S, Marsden AL (2011) A stochastic collocation method for uncertainty quantification and propagation in cardiovascular simulations. J Biomech Eng 133: 031001.
     


110. Perdikaris P, Grinberg L, Karniadakis GE (2015) An effective fractal-tree closure model for simulating blood flow in large arterial networks. Ann Biomed Eng 43: 1432-1442.
     


111. Linninger AA, Gould IG, Marinnan T, Hsu CY, Chojecki M, et al. (2013) Cerebral microcirculation and oxygen tension in the human secondary cortex. Ann Biomed Eng 41: 2264-2284.
     


112. Demiray H (2002) Propagation of weakly nonlinear waves in fluid-filled thin elastic tubes. Applied Mathematics and Computation 133: 29-41.
     


113. Yomosa S (1987) Solitary waves in large blood vessels. Journal of the Physical Society of Japan 56: 506-520.
     


114. Crepeau E, Sorine M (2007) A reduced model of pulsatile flow in an arterial compartment. Chaos Solitons & Fractals 34: 594-605.
     


115. Laleg TM, Crepeau E, Sorine M (2007) Separation of arterial pressure into a nonlinear superposition of solitary waves and a windkessel flow. Biomedical Signal Processing and Control 2: 163-170.
     


116. Lombardi D (2014) Inverse problems in 1D hemodynamics on systemic networks: A sequential approach. International Journal for Numerical Methods in Biomedical Engineering 30: 160-179.
     


117. Lee J, Smith N (2008) Development and application of a one-dimensional blood flow model for microvascular networks. Proc Inst Mech Eng H 222: 487-511.
     


118. Linninger AA, Xenos M, Sweetman B, Ponkshe S, Guo X, et al. (2009) A mathematical model of blood, cerebrospinal fluid and brain dynamics. J Math Biol 59: 729-759.
     


119. Morbiducci U, Ponzini R, Gallo D, Bignardi C, Rizzo G (2013) Inflow boundary conditions for image-based computational hemodynamics: Impact of idealized versus measured velocity profiles in the human aorta. J Biomech 46: 102-109.
     


120. Amblard A, Bou-Said B (2005) Modelling the blood flow in an aorta; the mptt and modified mptt models. Tribology and Interface Engineering Series 48: 381-387.
     


121. Apostolidis AJ, Moyer AP, Beris AN (2016) Non-newtonian effects in simulations of coronary arterial blood flow. Journal of Non-Newtonian Fluid Mechanics 233: 155-165.
     


122. Bessonov N, Sequeira A, Simakov S, Vassilevski Y, Volpert V (2016) Methods of blood flow modelling. Math Model Nat Phenom 11: 1-25.
     


123. Stein PD, Sabbah HN (1976) Turbulent blood flow in the ascending aorta of humans with normal and diseased aortic valves. Circ Res 39: 58-65.
     


124. Fernandez MA, Milisic V, Quarteroni A (2005) Analysis of a geometrical multiscale blood flow model based on the coupling of odes and hyperbolic pdes. Multiscale Modeling & Simulation 4: 215-236.
     


125. Fullana JM, Zaleski S (2009) A branched one-dimensional model of vessel networks. Journal of Fluid Mechanics 621: 183-204.
     


126. Holenstein R, Niederer P, Anliker M (1980) A viscoelastic model for use in predicting arterial pulse waves. J Biomech Eng 102: 318-325.
     


127. Raghu R, Taylor CA (2011) Verification of a one-dimensional finite element method for modeling blood flow in the cardiovascular system incorporating a viscoelastic wall model. Finite Elements in Analysis and Design 47: 586-592.
     


128. Raghu R, Vignon-Clementel IE, Figueroa CA, Taylor CA (2011) Comparative study of viscoelastic arterial wall models in nonlinear one-dimensional finite element simulations of blood flow. J Biomech Eng 133.
     


129. Reuderink PJ, Hoogstraten HW, Sipkema P, Hillen B, Westerhof N (1989) Linear and nonlinear one-dimensional models of pulse wave transmission at high Womersley numbers. J Biomech 22: 819-827.
     


130. Steele BN, Valdez-Jasso D, Haider MA, Olufsen MS (2011) Predicting arterial flow and pressure dynamics using a 1d fluid dynamics model with a viscoelastic wall. SIAM J Appl Math 71: 1123-1143.
     


131. Surovtsova I (2005) Effects of compliance mismatch on blood flow in an artery with endovascular prosthesis. J Biomech 38: 2078-2086.
     


132. Balar SD, Rogge TR, Young DF (1989) Computer simulation of blood flow in the human arm. J Biomech 22: 691-697.
     


133. Raines JK, Jaffrin MY, Shapiro AH (1974) A computer simulation of arterial dynamics in the human leg. J Biomech 7: 77-91.
     


134. Formaggia L, Nobile F, Quarteroni A, Veneziani A (1999) Multiscale modelling of the circulatory system: A preliminary analysis. Computing and Visualization in Science 2: 75-83.
     


135. Ruan WH, Clark ME, Zhao MD, Curcio A (2003) A hyperbolic system of equations of blood flow in an arterial network. SIAM J Appl Math 64: 637-667.
     


136. Taylor MG (1966) Wave transmission through an assembly of randomly branching elastic tubes. Biophys J 6: 697-716.
     


137. Wang X, Delestre O, Fullana JM, Saito M, Ikenaga Y, et al. (2012) Comparing different numerical methods for solving arterial 1D flows in networks. Computer Methods in Biomechanics and Biomedical Engineering 15: 61-62.
     


138. Batzel JJ, Timischl-Teschl S, Kappel F (2005) A cardiovascular-respiratory control system model including state delay with application to congestive heart failure in humans. Journal of Mathematical Biology 50: 293-335.
     


139. Kappel F (2012) Modeling the dynamics of the cardiovascular-respiratory system (cvrs) in humans, a survey. Math Model Nat Phenom 7: 65-77.
     


140. Kappel F, Fink M, Batzel JJ (2007) Aspects of control of the cardiovascular-respiratory system during orthostatic stress induced by lower body negative pressure. Math Biosci 206: 273-308.
     


141. Fink M, Batzel JJ, Kappel F (2004) An optimal control approach to modeling the cardiovascular-respiratory system: An application to orthostatic stress.Cardiovascular Engineering: An International Journal 4: 27-38.
     


142. Batzel JJ, Goswami N, Lackner HK, Roessler A, Bachar M, et al. (2009) Patterns of cardiovascular control during repeated tests of orthostatic loading. Cardiovasc Eng 9: 134-143.
     


143. Olufsen MS, Nadim A, Lipsitz LA (2002) Dynamics of cerebral blood flow regulation explained using a lumped parameter model. Am J Physiol Regul Integr Comp Physiol 282: R611-R622.
     


144. Huberts W, Van Canneyt K, Segers P, Eloot S, Tordoir JHM, et al. (2012) Experimental validation of a pulse wave propagation model for predicting hemodynamics after vascular access surgery. J Biomech 45: 1684-1691.
     


145. Willemet M, Lacroix V, Marchandise E (2013) Validation of a 1D patient-specific model of the arterial hemodynamics in bypassed lower-limbs: Simulations against in vivo measurements. Med Eng Phys 35: 1573-1583.
     


146. Formaggia L, Nobile F, Quarteroni A (2002) A one dimensional model for blood flow: Application to vascular prosthesis. In: Babuška I, Ciarlet PG, Miyoshi T, Mathematical modeling and numerical simulation in continuum mechanics, Springer, Berlin.
     


147. Smith N, Hunter P (2004) Giving form to the function of the heart: Embedding cellular models in an anatomical framework. Jpn J Physiol 54: 541-544.
     


148. Smith NP (2004) A computational study of the interaction between coronary blood flow and myocardial mechanics. Physiol Meas 25: 863-877.
     


149. Wang JJ, Parker KH, Tyberg JV (2001) Left ventricular wave speed. J Appl Physiol (1985) 91: 2531-2536.
     


150. Wang Z, Jalali F, Sun YH, Wang JJ, Parker KH, et al. (2005) Assessment of left ventricular diastolic suction in dogs using wave-intensity analysis. Am J Physiol Heart Circ Physiol 288: H1641-H1651.
     


151. Sun YH, Anderson TJ, Parker KH, Tyberg JV (2000) Wave-intensity analysis: a new approach to coronary hemodynamics. J Appl Physiol (1985) 89: 1636-1644.
     


152. Zambanini A, Cunningham SL, Parker KH, Khir AW, Thom SAM, et al. (2005) Wave-energy patterns in carotid, brachial, and radial arteries: A noninvasive approach using wave-intensity analysis. American Journal of Physiology-Heart and Circulatory Physiology 289: H270-H276.
     


153. Hollander EH, Dobson GM, Wang JJ, Parker KH, Tyberg JV (2004) Direct and series transmission of left atrial pressure perturbations to the pulmonary artery: A study using wave-intensity analysis. Am J Physiol Heart Circ Physiol 286: H267-H275.
     


154. Di Carlo A, Nardinocchi P, Pontrelli G, Teresi L (2003) A heterogeneous approach for modelling blood flow in an arterial segment. Advances in Computational Bioengineering 7: 69-78.
     


155. Pontrelli G (2004) A multiscale approach for modelling wave propagation in an arterial segment. Comput Methods Biomech Biomed Engin 7: 79-89.
     


156. Karniadakis GE (2016) Computational models of blood disorders. Drug Discovery Today: Disease Models.
     


157. Taelman L, Degroote J, Verdonck P, Vierendeels J, Segers P (2013) Modeling hemodynamics in vascular networks using a geometrical multiscale approach: Numerical aspects. Annals of Biomedical Engineering 41: 1445-1458.
     


158. Reymond P, Perren F, Lazeyras F, Stergiopulos N (2012) Patient-specific mean pressure drop in the systemic arterial tree, a comparison between 1-D and 3-D models. J Biomech 45: 2499-2505.
     


159. Epstein S, Willemet M, Chowienczyk PJ, Alastruey J (2015) Reducing the number of parameters in 1D arterial blood flow modeling: Less is more for patient-specific simulations. Am J Physiol Heart Circ Physiol 309: H222-H234.
     


160. Reymond P, Vardoulis O, Stergiopulos N (2012) Generic and patient-specific models of the arterial tree. J Clin Monit Comput 26: 375-382.
     


161. Morbiducci U, Gallo D, Massai D, Consolo F, Ponzini R, et al. (2010) Outflow conditions for image-based hemodynamic models of the carotid bifurcation: Implications for indicators of abnormal flow. J Biomech Eng 132.
     


162. Pant S, Fabreges B, Gerbeau JF, Vignon-Clementel IE (2014) A methodological paradigm for patient-specific multi-scale CFD simulations: From clinical measurements to parameter estimates for individual analysis. International Journal for Numerical Methods in Biomedical Engineering 30: 1614-1648.
     


163. Chandra S, Raut SS, Jana A, Biederman RW, Doyle M, et al. (2013) Fluid-structure interaction modeling of abdominal aortic aneurysms: The impact of patient-specific inflow conditions and fluid/solid coupling. J Biomech Eng 135.
     


164. Devault K, Gremaud PA, Novak V, Olufsen MS, Vernières G, et al. (2008) Blood Flow In The Circle Of Willis: Modeling And Calibration. Multiscale Model Simul 7: 888-909.
     


165. Reymond P, Bohraus Y, Perren F, Lazeyras F, Stergiopulos N (2011) Validation of a patient-specific one-dimensional model of the systemic arterial tree. Am J Physiol Heart Circ Physiol 301: H1173-1182.
     


166. Stettler JC, Niederer P, Anliker M (1981) Theoretical analysis of arterial hemodynamics including the influence of bifurcations. Part 1: Mathematical model and prediction of normal pulse patterns. Annals of Biomedical Engineering 9: 145-164.
     


167. Xiu DB, Sherwin SJ (2007) Parametric uncertainty analysis of pulse wave propagation in a model of a human arterial network.Journal of Computational Physics 226: 1385-1407.
     


168. Leguy CAD, Bosboom EMH, Gelderblom H, Hoeks APG, van de Vosse FNV (2010) Estimation of distributed arterial mechanical properties using a wave propagation model in a reverse way. Medical Engineering & Physics 32: 957-967.
     


169. Johnson DA, Rose WC, Edwards JW, Naik UP, Beris AN (2011) Application of 1D blood flow models of the human arterial network to differential pressure predictions. J Biomech 44: 869-876.
     


170. Morbiducci U, Kok AM, Kwak BR, Stone PH, Steinman DA, et al. (2016) Atherosclerosis at arterial bifurcations: evidence for the role of haemodynamics and geometry. Thromb Haemost 115: 484-492.
     


171. van der Horst A, Boogaard FL, van't Veer M, Rutten MC, Pijls NH, et al. (2013) Towards patient-specific modeling of coronary hemodynamics in healthy and diseased state.Computational and Mathematical Methods in Medicine 2013.
     


172. Guala A, Camporeale C, Tosello F, Canuto C, Ridolfi L (2015) Modelling and subject-specific validation of the heart-arterial tree system. Ann Biomed Eng 43: 222-237.