Background: Considerations must be taken when designing group-randomized trials due to the hierarchical structure of the data. Longitudinal group-randomized trials have an added layer of nesting adding more complexity to the study design. Simulation studies have been performed to compare the operating characteristics and validate statistical models for these hierarchical data structures, but many provide simulations from parametric distributions under set assumptions.
Methods: Our manuscript aims to use previous study data to compare two statistical analysis methods in group-randomized trial designs through data-driven simulations for a prospective study design. Creating simulated datasets using existing study data from a previous study allows the existing data to drive the assumptions of the models. The motivation for this simulation study was a potential concern that our proposed longitudinal mixed-effects model could have inflated type I error. We compare the empirical power and type I error rate for our proposed model against a baseline adjusted model at a single time point when modeling a continuous outcome, % weight change at 24 months. The longitudinal model includes three follow-up time points, while the other models the outcome with an adjustment for a baseline measure, weight. The empirical power of the models is calculated and compared for varying effect sizes.
Results: Results showed that the models had comparable power for the tested effect sizes and type I error rates of 3.09% and 3.87% for the longitudinal and the baseline adjusted model, respectively. Conclusion
These results show our proposed longitudinal model does not result in an inflated type I error rate and would be sufficient to use for the future trial.
Cluster-randomized, Simulated trial design, Comparative effectiveness, Existing study data, Prospective study design
ICC: Infraclass Correlation
Group-randomized clinical trial designs, also commonly referred to as cluster-randomized clinical trial designs, randomize groups of subjects rather than individuals to study conditions, creating a hierarchical data structure as the subjects within a cluster are correlated. This correlation violates the independence assumption and is measured by the intracluster, or intraclass, correlation (ICC), defined as the ratio of the between-cluster variance to the total variance [1]. Group randomization is the only feasible method for randomization when an intervention must be applied to an entire group. These trial designs are now a key tool in the comparative effectiveness of treatments in health services research and implementation science as they can be more administratively convenient, increase subject compliance, reduce contamination bias, and produce results applicable in real-world clinical settings [2-4]. An added level of hierarchical, or nested, data occurs in longitudinal group-randomized trial designs. As the subjects are measured more than once throughout the study, the repeated measurements are correlated or exhibit variability that changes. Although there are many benefits to group-randomized trial designs, they pose some design and analysis problems not present in other designs [4]. As these group-randomized trial designs are more widely used, there is more available literature that has been published to address these issues in design and analysis, many using simulations studies [5-9].
Simulation studies are an invaluable tool for statistical research, particularly for the comparison of the performance of statistical methods [10]. Simulation studies use pseudo-random sampling to generate datasets, and these simulated datasets are used to obtain empirical results that allow comparison between different statistical models [10]. The pseudo-random sampling can be performed either by producing parametric draws from a known model or by data-driven sampling methods. Re-sampling with replacement, is sampling many simulated datasets with replacement from a specific dataset and is based on the idea that using existing data instead of making assumptions about the populations one is attempting to estimate can give better results [11].
Although the literature is rich with manuscripts that use distribution-driven simulations to evaluate the performance of modeling techniques and provide recommendations on adequate sample sizes and the total number of clusters, our paper aims to provide an example of using a simulation study using re-sampling with replacement on previous study data to compare statistical methods [12]. Our motivation for this paper came from a concern about a recently funded grant that was written to expand on lessons learned in a previous trial, RE-POWER (Rural Engagement in Primary Care for Optimizing Weight Reduction) [13,14]. The proposed grant used a repeated measures mixed model with three-time points modeled explicitly, similar to what was used in RE-POWER, but the reviewer noted that Murray et al. showed through simulations that this model design is known to have an inflated type 1 error, up to 20%, depending on the simulation assumptions [6]. Several alternative models could be used in this case, including a mixed-effects model at a single follow-up time with an adjustment for baseline measure or a random coefficients analysis that would include all of the time points [6].
The primary goal of this manuscript is to compare the model we proposed, a mixed-effect repeated measures model with three-time points, by comparing it to a mixed-effects model at a single follow-up adjusting for baseline. The prospective study structure is very similar to the previous study, RE-POWER, so we have a unique opportunity to use the existing study data and simulation studies to compare the two analytic methods by allowing the simulated data to drive the assumptions that other simulation techniques must specify.
The rest of this article is organized as follows. In Section 2, we present the information from the previous study that provides the data from which we derived the simulated datasets used to perform our simulation studies. The information for the prospective study that will set up our simulation datasets is also provided. The statistical mixed effect models for the clustered data are presented in Section 3. Section 4 details the structure of the simulations, then the simulation results are presented in Section 5, followed by the concluding remarks in section 6.
Capitalizing on the expanded capacity for home-based telemedicine and lessons learned in a previous primary care-based weight-loss trial, we are currently conducting a cluster-randomized trial, RE-TOOL (Rural Engagement in Teemed Team for Options in Obesity Solutions). The previous study, RE-POWER, was a pragmatic cluster randomized trial across 36 primary care clinics that ended in January 2020 with the primary care clinics as the randomization unit. There were three treatment groups compared; two were a group-based intervention (one in person, one telehealth), and the third group included individual in-person clinic visits with clinicians. There were 1407 participants enrolled across the 36 primary care clinics that were randomly assigned to the treatment arms, with most clinics accruing 35-40 participants. The primary outcome, weight loss, was measured at 6, 18, and 24 months. Follow-up data were complete for 91.7%, 84.6%, and 86.7% of participants at 6, 18, and 24 months, respectively. Analyses used linear mixed-effects multilevel models, including random participant and cluster (practice) effects, to explore the differences in the outcome of absolute weight change and percentage weight change at 24 months with model adjustment for randomization strata. The most efficient covariance structure based on Akaike’s information criterion (AIC) was used. Upon comparing the models' AICs to determine the covariance structure that provided the best relative goodness-of-fit, we found the variance components structure to be best to describe the random effect of site and unstructured to be best for describing the correlation in participants' measures. The missing outcomes were treated as missing at random and addressed using maximum likelihood methods. The intraclass correlation coefficient for the participants within the clusters for RE-POWER was found to be 0.02.
The prospective study, RE-TOOL, will compare the percent weight change between two interventions: Team Care which combines intensive group-based coaching visits with quarterly individual team-based clinic visits, and Local Care + which has quarterly primary care physician visits only. We propose a total of 16 clinics, randomized 1:1 to the two treatment groups, which will accrue 35 participants per clinic. Percent weight change from baseline will be captured at three-time points, 6, 12, and 24 months with a hypothesized net between-group treatment effect at 24 months of 3%. Using a closed analytic formula and a type I error rate of 0.05, the trial will have 85% power to detect a net between-group treatment effect of 3% (SD = 8%) with an ICC of 0.02, as observed in RE-POWER. We planned to use similar analysis techniques that were used in RE-POWER, and percent weight loss would be analyzed using hierarchical linear mixed-effects models using weights at 6, 12, and 24 months, with intervention arm, time, clinic, and their interaction terms included in the model. In the absence of differential loss to follow-up, the primary analysis described above will use restricted maximum likelihood, and no participants will be deleted from the analysis due to missing data.
Mixed models are an extension of simple linear models to allow both fixed and random effects to be included in modelling the outcome. Mixed models are used in group-randomized controlled trials due to the nested structure of participants within randomized clusters. The continuous outcome measure of interest is the percent weight change, specifically at 24 months, defined as the quantity 24 month weight-baseline weight divided by baseline weight.
A three-level mixed-effects repeated measures linear model for our continuous outcome, % weight change , with subject-specific and cluster-specific random slopes can be written as
where is the index for the participant within the k th cluster, . The variable is the intervention assignment indicator for participant i , coded 1 for the treatment (Team Care) and 0 for the comparison group (Local Care +) . Since the randomization to the treatment is done at the site level (cluster), the index for will only depend on k . The variables take a value of 1 for the i th participant’s 18 month or 24-month weight change, respectively, and 0 otherwise. The fixed effect terms in equation (1) include the overall fixed intercept, denotes the effect of the treatment group at the 6 month follow-up time, and denote the time effects in the comparison group for 18 and 24 months, respectively and and denote the intervention by time interaction effects, which can be interpreted as the additional change in the % weight change for the treatment group over time compared to the comparison group. To account for the positive intraclass correlation expected in the data, the cluster- and participant-specific random effects must be specified in the model. It has been shown that failing to include these effects will result in an inflated type I error rate [14,15]. The random effects allow for correlation among members within a site, , and across time, and , for correlation among participants and across time and , and for random variations among the participants, Under the general linear mixed model, we assume that the random effects are independent and normally distributed as , and . The null hypothesis we will be testing is that there is no treatment effect, in % weight change at month 24 when adjusting for baseline weight.
The null hypothesis we will be testing is that there is no difference in outcome, % weight change, between the two treatment groups at month 24, .
In the alternative baseline-adjusted model, we are modelling a single follow-up time with adjustment for baseline weight. The mixed-effects linear model for % weight change at month 24 with subject-specific and cluster-specific random slopes and an adjustment for baseline weight can be written as
where is the index for the participant, nested within the k th cluster, . The variable is the intervention assignment indicator for participant i , coded 1 for the treatment and 0 for the comparison group. Since the randomization to the treatment is done at the site level (cluster), the index for will only depend on k . The variable denotes the baseline weight measured for participant i . The fixed effect terms in equation (1) include the overall fixed intercept, denotes the treatment effect for the outcome, % weight loss at month 24, and denotes the slope of the baseline weight effect in the comparison group, i.e., the change in the intervention effect for a one-unit change in baseline weight. The random effects allow for correlation among members within a site, , for correlation among participants , and random variations among the participants, Under the general linear mixed model, we assume that the random effects are independent and normally distributed as , and . The null hypothesis we will be testing is that there is no treatment effect, in % weight change at month 24 when adjusting for baseline weight.
We performed simulation studies to compare the empirical type I error rate and power for the two models described in Section 3 under different effect size scenarios. We used simple random sampling to draw sites from the previous study data, drew participants from the selected sites with replacement, and assigned the selected sites to the treatment arm (Team Care) or comparison arm (Local Care + ) in 1:1 using a null distribution. For the type I error rate, we modeled the simulated data without any adjustments to the % weight change variable, i.e., see the no effect scenario in (Table S1).
Table 1: Simulated percent weight change for treatment (Team Care) and comparison (Local Care+) for the hypothesized effect. View Table 1
To calculate the empirical power, we adjusted the % weight change for the participants at the clinics randomized to the treatment group by subtracting the values in Table S1 from the % weight change for each participant at the treatment arm sites. For instance, the simulated data before adjustments were made for the treatment group arm had a 24-month mean % weight change of -4.37%, thus after the adjustment for the hypothesized effect (Scenario 4), the 24-month mean % weight change would be -7.37%. The % weight change effect size was adjusted for a greater % weight change at the earlier time points, months 6 and 12, as the previous study showed participants initially had a greater % weight loss early in the study that was trending back toward 0% as the study went on. Table S1 shows the adjustments that were made to the % weight change for the participants allocated to the Team Care arm for each of the follow-up time periods before modelling the data again.
The formal steps for the data set generation are:
S1. Randomly sample with replacement 16 clinics from the 34 clinics in our data set.
S2. For each clinic, randomly generate the intervention assignment indication or 1. Note that we are considering a balanced allocation of the intervention.
S3. Randomly sample without replacement 35 participants % weight change for each follow-up time and the baseline weight from the 16 selected clinics.
S4. Adjust the % weight change in the simulated dataset depending on the follow-up time to the values shown in Table 1 for each of the scenarios.
S5. Fit the data with the three-level linear mixed effects model (1) using the MIXED procedure in SAS/STAT TM software [16]. Code provided in Appendix A.
S6. The p -value, p 1sd , for the pairwise test of the treatment group to the comparison group at the month 24 follow-up is obtained for the d th simulated dataset for the s th scenario.
S6. Fit the data with the two-level linear mixed effect model with the adjustment for baseline weight (2) using the MIXED procedure in SAS/STAT software. The covariance structure is the default variance components. Code is provided in Appendix A.
S7. The p -value, p 2sd, for the test of the treatment effect, is obtained for the d th simulated dataset for the s th scenario.
S9. Repeat steps S4 to S8, storing the p -values from each of the effect size adjustments for scenarios (2)-(6) in (Table 1).
S10. Repeat steps S1 to S9 10,000 times for each combination of effect size modification. Thus, we have p -values from 10,000 simulated datasets for the original sampled datasets and each of the effect size adjustments.
S11. Calculate the empirical power (or type I error rate) as the proportion of times the simulation-based p -value is smaller than the significance level, α = 0.05.
By using 10,000 simulated data sets to compare our two models, the maximum margin error is
The simulation study produced 10,000 sampled datasets from the RE-POWER study data, with each having a total sample size of 560 participants across 16 sites, with each site having 35 participants. Since the simulated data was drawn from the RE-POWER population, we expect the missing data to be about 8.3%, 15.4%, and 13.3% for months 6, 12, and 24, respectively. Across these samples, the treatment group arm had a 24-month mean % weight change of -4.37% (SD = 8.48%) compared to the comparison groups of -4.39% (SD = 8.51%). This results in a bias of 0.02, favouring the comparison arm. The empirical type I error rate was calculated for no effect of treatment (null) and the empirical power was calculated for the effect sizes or a difference in % weight change comparing treatment to comparison, 1, 2, 3, and 4%. These values were found by calculating the number of times out of 10,000 that the p -value of the pairwise test was less than 0.05. Figure 1 provides the empirical type I error rate (effect size of 0%) and the empirical power comparison for the two statistical methods for the varying effect sizes. It shows that for all assumed effect sizes, the power is very comparable, although slightly lower in the longitudinal model. For our specific hypothesized effect size, 3%, the longitudinal model has empirical power of 84.28% compared to 86.09% in the baseline-adjusted model.
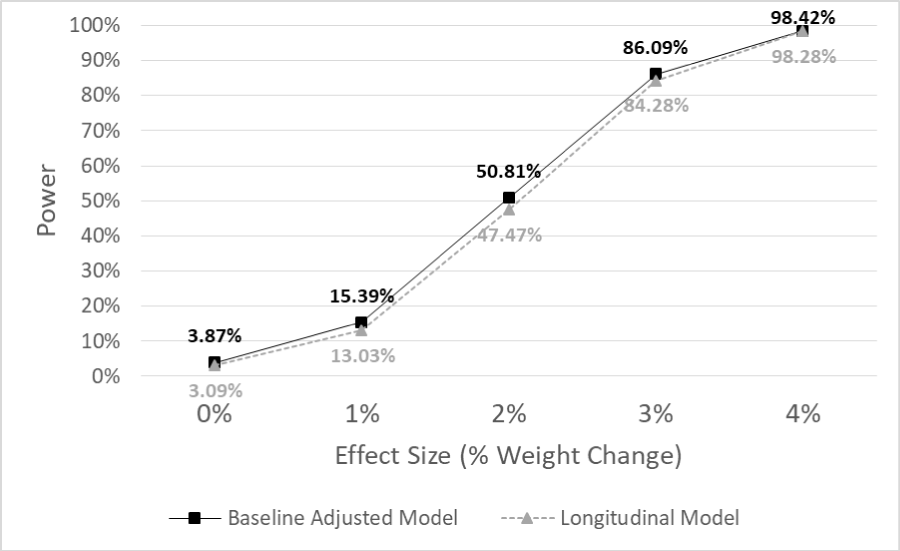 Figure 1: A plot of empirical power for each of the two models we are comparing for the varying effect sizes for % weight change at 24 months. The proposed prospective study, RE-TOOL, has a hypothesized effect size of 3% at 24 months.
View Figure 1
Figure 1: A plot of empirical power for each of the two models we are comparing for the varying effect sizes for % weight change at 24 months. The proposed prospective study, RE-TOOL, has a hypothesized effect size of 3% at 24 months.
View Figure 1
Although the power is slightly lower in the longitudinal arm, the type I error rate is also lower in the longitudinal model, 3.09%, compared to 3.87% in the baseline-adjusted model. The primary effect size of interest was 3%, as the prospective study hypothesized that the treatment group would have an average % weight loss of 3% more than the comparison arm. For the pairwise test of treatment group vs. comparison group % weight change at month 24, the mean estimate across the simulations was -2.97% for the longitudinal model compared to -2.98% for the baseline adjusted model. The coverage probability for our hypothesized effect size was found to be 96.21% [95% CI: 96.58-95.84] compared to 94.15% [95% CI: 93.69-94.61] for the longitudinal and baseline adjusted model, respectively.
In this manuscript, we used simulation studies using the data-driven method to challenge the proposed statistical model originally proposed. The simulation results showed the empirical power and type I error rate comparison between the proposed longitudinal statistical model and the single time point, baseline-adjusted model. Although the baseline-adjusted model was slightly more powerful for the hypothesized time effect, we did find that the empirical type I error rate was not inflated in the longitudinal model. The coverage probability and estimated mean difference between the two groups also favoured the longitudinal model. The results from this simulation study provide justification to move forward with the longitudinal mixed model if we wish to keep consistent with the analysis and results presented in the previous, very similar study.
Murray, et al. concluded that the longitudinal mixed-effect models were still useful under certain assumptions compared to a baseline adjusted model. By allowing the previous study data to drive the assumptions of our modelling, we found the longitudinal model across three-time points to still be useful. Having the ability to use previous study data to design or compare statistical methods for a future trial is a unique opportunity. Our study provides an example of performing a simulation study using previous study data to compare statistical methods. Some limitations include borderline small number of clusters utilized for this study design and the approach used in the paper is that it cannot be used in situations where previous study data does not exist or the new study design deviates too far from the previous study design.
We would like to thank the RETOOL grant reviewer that prompted this work.
Research reported in this publication was supported by the National Cancer Institute under Award Numbers R01CA268034 and P30CA168524. The data from this study comes from a contract from the Patient Cantered Outcomes Research Institute (PCORI), RE-POWER Study #OB-1402-09413. The contents are solely the responsibility of the authors and do not necessarily represent the official views of the NIH/NCI/PCORI.
AB performed the coding and simulation analysis. BG conceptualized the idea. MM provided a thorough review of the methods used. EE and CB provided the study design for the prospective and previous study.
The datasets used during the current study are not publicly available but are available from the corresponding author on reasonable request.
The authors declare that they have no competing interests.