Biomarker targeted two-stage adaptive design is used increasingly in early-stage clinical trials in a variety of therapeutic areas including oncology, where the sample size of the trial is re-estimated based on the first stage data. In such trials often the sample size is moderate, and so incorporating prior information and using robust methods are desirable. In this article, to improve upon existing methods using parametric normal models, we propose a nonparametric Bayesian approach for designing such adaptive trials in a phase IIb/IIIa setting comparing a treatment vs. a control. Extensive simulation studies are conducted to evaluate the performance of the proposed method and compare it with the existing normal parametric model. Our results indicate that with good prior information, more reasonable and robust inference than with existing parametric methods can be obtained.
Adaptive design, Biomarker targeted design, Maximum likelihood estimate, Non-parametric Bayes model, Sample size, Two-stage clinical trial
Biomarker targeted design is an important step towards precision medicine, which can improve efficiency of randomized clinical trial [1,2]. Zhou, et al. [3] and Lee, et al. [4] proposed Bayesian approach and Wang, et al. [5] applied this design in therapeutic trials, Freidlin, et al. [6] discussed issues with this design, Tang and Zhou [7] proposed a general framework. The two or three stage designs are commonly used in recent phase IIb-IIIa trials comparing treatment vs. control. Such sequential monitoring has become an integral part of clinical trial. It allows for early stopping of the trial for extreme results observed in interim stage(s) [8-11].
More recently, Gao, Roy, and Tan [12,13] proposed a two-stage adaptive design for biomarker targeted population where only biomarker positive subjects enter the trial study. However, the test is imperfect subject to false positive and false negative errors. Thus a mixture normal model is used for the biomarker positive subjects. The final sample size re-estimation is based on the positive predict value (PPV), the proportion of true positives among test positives, estimated from the first stage data, deviates slight from a more common adaptive designs [14-16]. Proschan [17] and Xiong, Tan and Boyett [18] discussed sample size re-estimation in clinical trials. Since for early-stage clinical trial, often the sample size is relatively small, and so incorporating valuable prior information, if available, and using a robust method would be desirable. For the first goal a Bayesian model is preferable, while for robustness the nonparametric method is more suitable. Thus, we propose a nonparametric Bayesian method to achieve both goals.
The rest of this article is organized as follows. Section 2 introduces the problem, then develops the proposed nonparametric Bayesian method, and compares with the frequentist parametric method, the two-stage sequential test, and sample size re-estimation. In Section 3, extensive simulation studies are conducted to evaluate the performance of the proposed method, compared it with the existing normal parametric model. We leave the technical details in the Appendix.
We first introduce the setting by briefly reviewing the related targeted design in Gao, Roy, and Tan [13]. Consider a two-stage clinical trial with continuous or response endpoint comparing two groups, control and treatment, to assess the effect of a new treatment. The observed data at stage k is from independent biomarker test positive individuals (k = 1, 2), xCi is response from the i-th individual in the control group, and xTj is that from the control group. By convention, the sample size nC2 and nT2 include nC1 and nT1; n1 = nC1 + nT1 is the planned sample size for stage I; and n2 = nC2 + nT2 is the total sample size at end of the trial, which is subject to updating based on parameters estimates from stage I data. Let μC be the mean response of the control group, μT be that for the treatment group, and θ = μT - μC be the treatment difference in the overall study population. The objective of the trial is to test whether there is treatment difference between the two arms, i.e. to test H0 : θ = 0 versus HA : θ ≠ 0, with pre-specified significance level α and power β, and determine the total sample size n2.
Since only biomarker test positive patients enter the trial, and a proportion ω of them are truly positive. Hence the trial population consists of true biomarker enrichment group (E) and the non-enrichment (NE) group. Let μ0C and μ1C be the mean response for NE and E group in control arm respectively; μ0T and μ1T be those for NE and E portion in the treatment arm respectively, and μC and μT be those of the control and treatment groups. Then
In Gao, Roy and Tan [13], the following normal mixture model are used
where Bi ~ Bernoulli (ω).
Let and be the sample means of the control and treatment group at end of stage I,
Then the total sample size n2 needed for the whole trial is estimated as
Maximum likelihood estimation (MLE) for mixture model is more conveniently obtained by the EM algorithm, given in the Appendix.
For early-stage clinical trial often the sample size is relatively small, and in some cases there is prior knowledge about the data distribution. A subjectively specified parametric model however may not be able to describe the distribution, so a nonparametric prior is preferred. Thus we adopt a nonparametric Bayesian model for this problem.
Let FC and FT be the distribution function of the control and treatment arm respectively. Often there are prior information for them. Let π(FC) and π(FT) be their priors, we assume and where is the Dirichlet process with parameter PC(.); similarly for The distribution PC is the prior knowledge about FC, and similarly for PT.
We adopt the following assumptions assumed in Gao, Roy and Tan [13].
A1) μ0C = μ1C = μ0T := μC;
A2) Var(X0C) = Var(X1C) = Var(X0T) = Var(X1T) := 2.
The reason for A1) is that a predictive biomarker is associated with response or lack of response to a particular therapy. Ideally, a predictive biomarker positive patient receiving therapy is expected to show a substantially higher response than negatively-biomarker patients receiving the therapy as well as those in the control group regardless of the marker status. Therefore, A1) with the treatment potentially making μ1T different from μ0C, μ1C and μ0T. Thus, the treatment effect, if any, is assumed to be a result of differential response to the treatment in the positively-biomarker group. A2) is a reasonable assumption to reduce model complexity.
For notational brevity, we will just write nC for nC,1 and nT for nT,1 etc. At end of stage I, using the non-parametric Bayesian formula for mean [19], in our case we have for μC and μT
where μPC and μPT are the prior means of PC and PT. We have the estimates for means of the two distributions
Also, using the non-parametric Bayesian formula for variance [19], we have of Var(XC) and of Var(XT ) in our case as
where is the prior second moment, similarly for
To update the estimation of PPV ω, let be the total responses at end of stage I. Since we substitute means and total responses to estimate ω as
For given significance level α and power β, the decision boundaries are determined to satisfy type I error no greater than α and with power at least β. Consider test statistics Tj at stage j (j = 1, ..., k), the flexible class of boundaries proposed by Wang and Tsiatis [20] are, for some (c, γ) to be determined,
Under H0, (T1, ..., Tk) is multivariate normal distributed with zero mean vector. The sequential test will reject the null hypothesis at stage j if |Tj| ≥ bj. Then we have equation
Here we adopt O'Brien-Fleming boundaries having shape parameter γ = 0. In our case, k = 2, α = 0.05, c = 2.7967. The corresponding threshold of p-value at stage I is approximately 0.0054.
If the null hypothesis is not rejected at stage I, the sample size for the next stage need be determined by considering the required global power. Recall that n1 and n2 are the sample sizes at the end of stage I and II respectively. For simplicity we assume nT = nC = n1/2. Then under H0,
Under H1,
with family-wise power function
Denote and which is determined by n2 given other parameters. Then n2 is determined by the least integer satisfies
Extensive simulation studies are conducted to compare three methods, the method of Gao, Roy and Tan [13], the proposed nonparametric Bayesian method, and the parametric maximum likelihood (MLE) based method. We considered both truncated normal and skewed normal (with skewness parameter α). The reason for the first is that the treatment effects should be negative values; the latter represent departure from the normality assumption. For the sequential test, we assume n1 = n2/2, i.e., the sample sizes are the same for the two stages. If the re-estimated sample size is less than n2, we will keep the original design. Moreover, the estimation of can be obtained using the formula below
which is the formula we actually used in the simulation study.
The results are displayed in Table 1, Table 2, Table 3, Table 4 and Table 5, with different parameter settings and sample sizes, with estimated treatment effects μT, μC, their difference θ, test result, and estimated sample size (if the null hypothesis is not rejected in stage I), the probability of reject H0 (so not continue the trial to stage II). In all the tables, results from the method of Gao, Roy and Tan [13] is named `empirical'; the proposed method, named `NP Bayes', and the MLE with EM-algorithm, named `MLE(EM), are compared. The sample size estimate n2 depends on the estimated PPV is not stable. So we display the mean, median and trimmed mean (with trim proportion 10% on both sides) from all three methods, with 500 repetitions. Also, the corresponding disease prevalence (prev), sensitivity (sen), specificity (spec), the true ω0, and the effect size (EF, |mean| /s.d) used in the simulation are given at the top of each Table.
Table 1: Estimation results from three methods (data from truncated-normal). View Table 1
Table 2: Comparison between different response rate (Truncated-normal). View Table 2
Table 3: Comparison in different scales (Skewed-normal). View Table 3
Table 4: Comparison in different sample sizes (Skewed-normal). View Table 4
Table 5: Comparison in different sample sizes (Skewed-normal). View Table 5
To reflect the effects on estimated sample size of the skewness of the skewed normal and of EF, Figure 1, Figure 2, Figure 3 and Figure 4 are shown for the mean and trimed mean estimation methods below. We see that the empirical Bayesian estimate seems more reasonable, the empirical methods tend to over-estimate the sample size, and the MLE tends to under estimate it, and that the trimed mean method is much more stable. For comparison, we altered settings for parameters and kept EF the same for each graph.
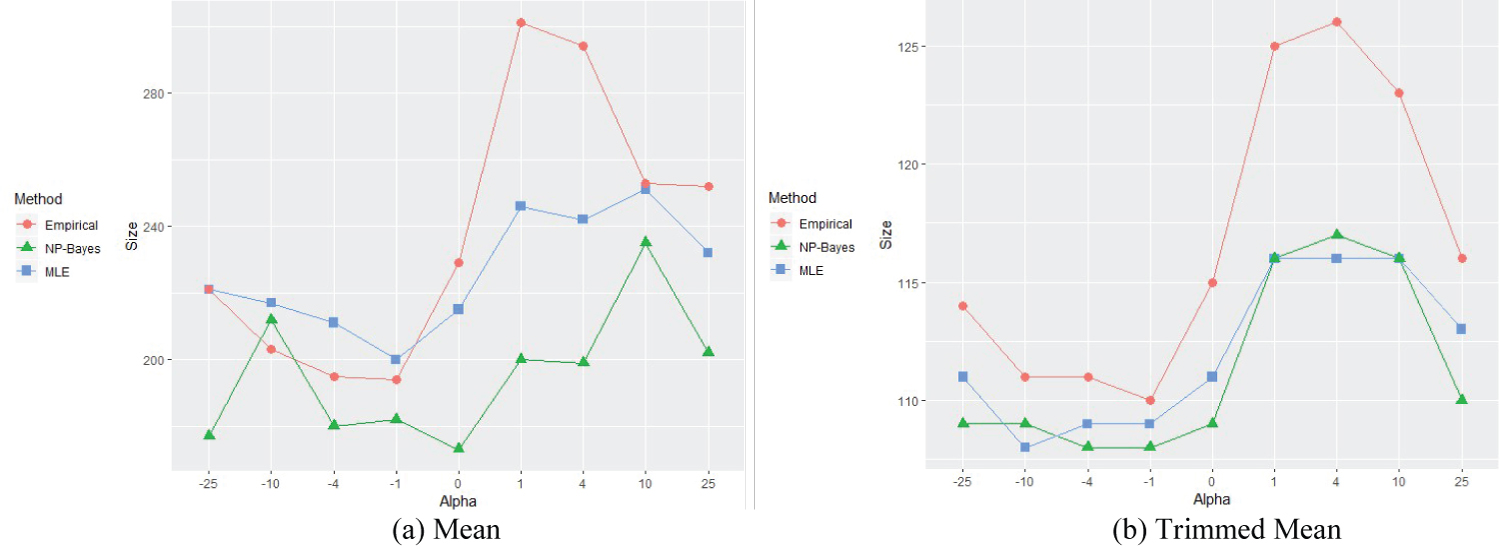 Figure 1: Means for different alpha settings (Table 3), EF = 0.81.
View Figure 1
Figure 1: Means for different alpha settings (Table 3), EF = 0.81.
View Figure 1
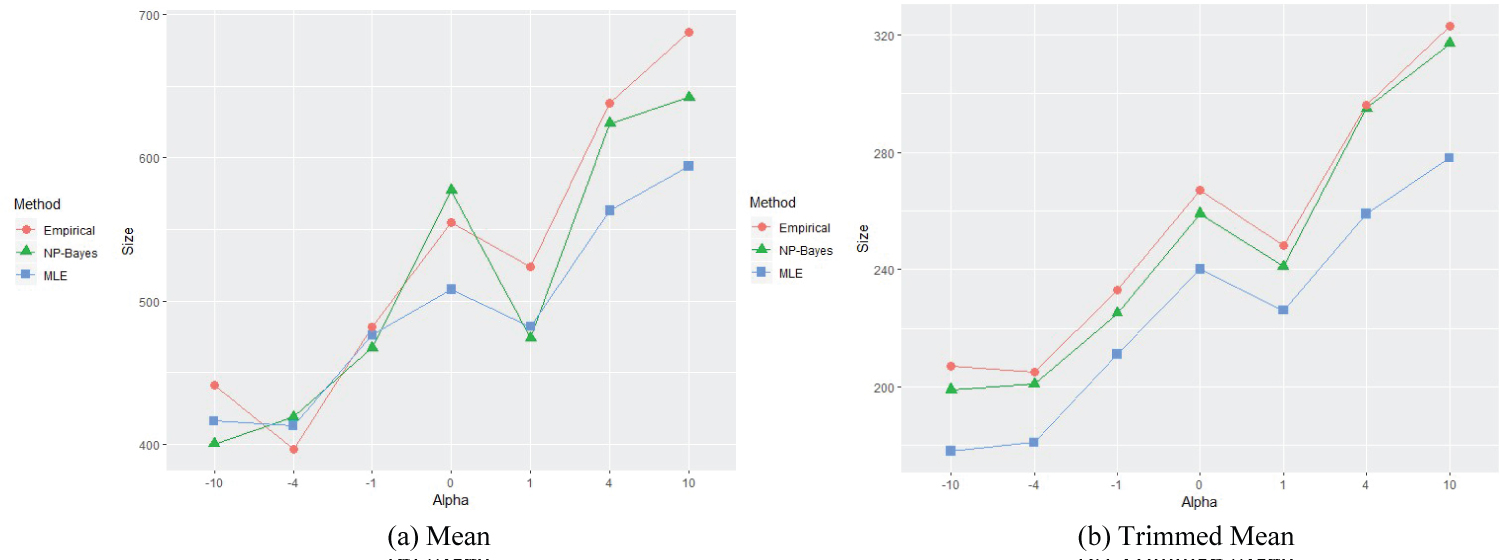 Figure 2: Means for different alpha settings, EF = 0.485.
View Figure 2
Figure 2: Means for different alpha settings, EF = 0.485.
View Figure 2
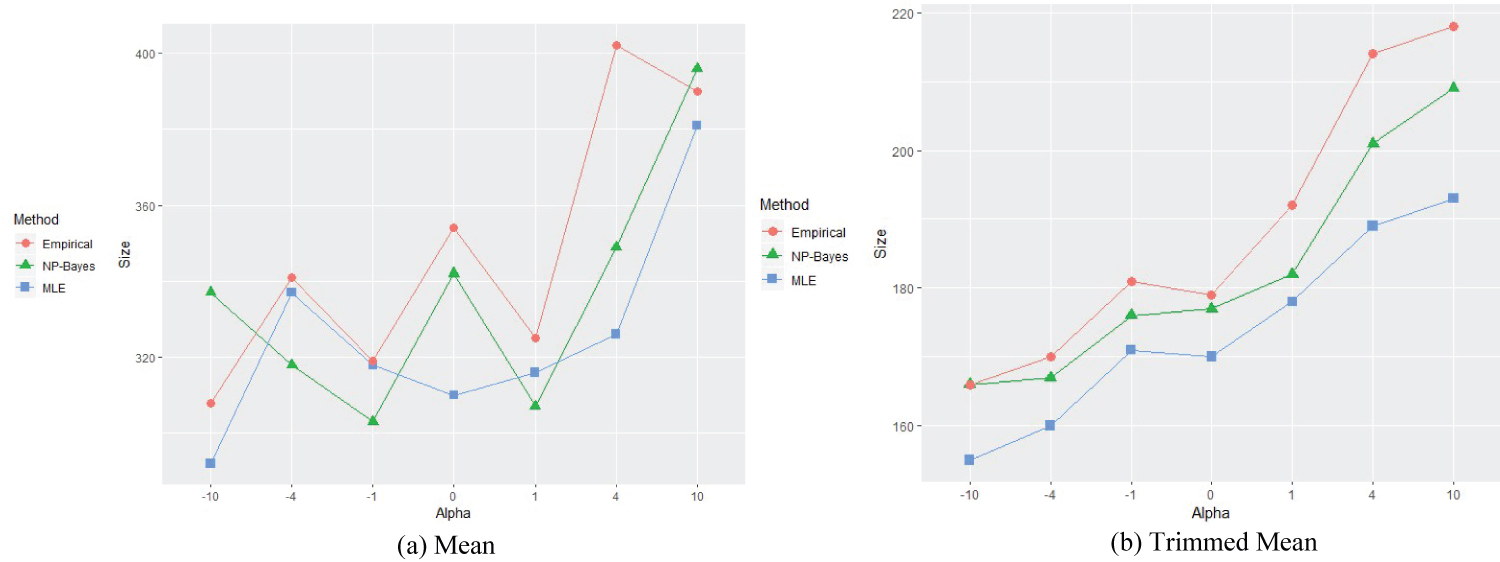 Figure 3: Means for different alpha settings, EF = 0.603.
View Figure 3
Figure 3: Means for different alpha settings, EF = 0.603.
View Figure 3
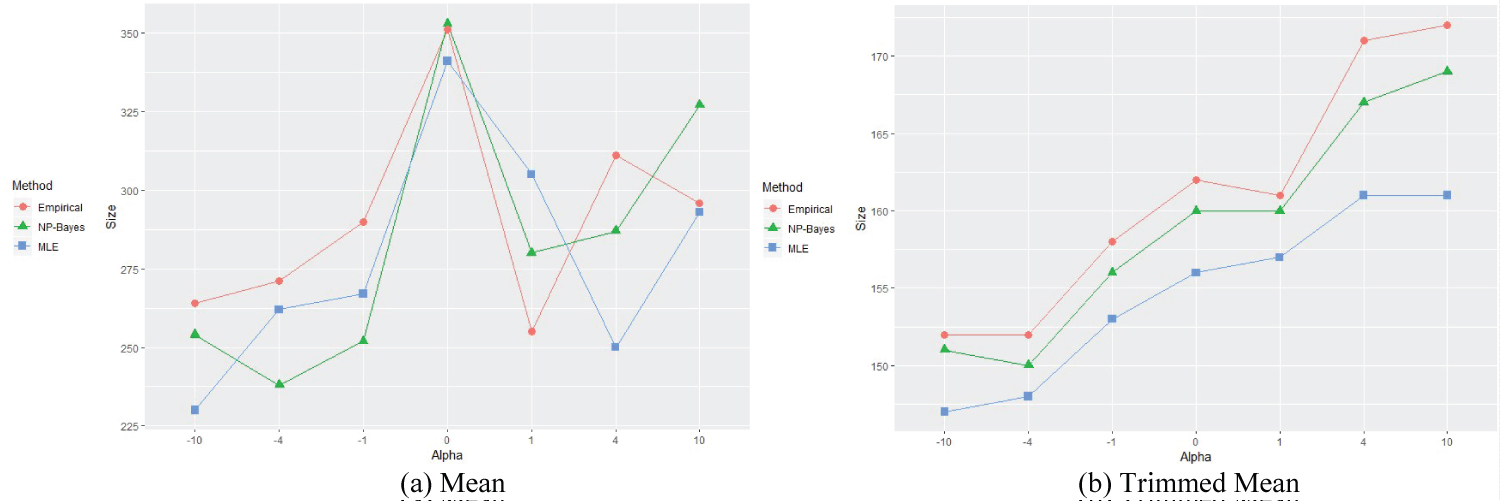 Figure 4: Means for different alpha settings, EF = 0.699.
View Figure 4
Figure 4: Means for different alpha settings, EF = 0.699.
View Figure 4
From the Tables, the empirical and non-parametric Bayesian estimates are close to each other when the sample size is relatively large, which is consistent with the Bayes-frequentist estimation theory. However, the non-parametric Bayesian estimators were more robust than empirical ones, especially in cases where the sample size is relatively small. The variance of the empirical estimators was hugely inflated, which would require large increase of patients in stage-II. Moreover, as expected the non-parametric Bayesian estimators were not very sensitive to the selection of the prior, likely due to the fact that essential information was captured by the prior already. MLE method by EM algorithm can give smallest increase in sample size, especially when the sample were precisely from normal distribution, with zero-skewness. However, the estimators were significantly biased, which may be caused by the exceedingly high power of the stage-I test than the specified level. Therefore, non-parametric Bayesian estimators performed the best in the proposed adaptive design since they are more robust and require weak assumption on prior. They utilize the prior information but are not too dependent on prior selection. In smaller scales, it could reduce the unexpected variance, which may lead to large sample size increase in the next stage. In addition, they asymptotically converged to empirical estimators, indicating unbiasedness with large sample sizes.
We have proposed a nonparametric Bayesian method for the two-stage adaptive biomarker-targeted clinical trial design. Compared with the existing parametric model, it has the advantage of incorporating prior information into the design, and being robust to model assumption. Extensive simulation studies are conducted to evaluate the performance of the proposed method, and compare with the commonly used methods for this problem. In our simulation studies, we considered the non-skewed and skewed, to reflect correct and incorrect model specifications. It was found that the skewness will influence the estimation accuracy in this design. The estimate is most accurate with left-skewed distributions, least accurate with right-skewed distributions, and modest with truncated normal distributions. Cases gave moderate results, and would be the hardest to estimate. Moreover, the more left-skewed, the more accurate for the estimations.