The accurate detection of vascular bifurcations is not helpful for pulmonary vascular disease diagnosis, but vital in (Computed Tomography) CT image analysis and processing of lung. We propose a tensor voting based method for vascular bifurcation detection in CT image of lung, which a vessel enhancement method is firstly proceeding to initially extract vessel structure, on which we perform ball voting with the pixels. Then counting the number of votes of each pixel and calculating the local maximum value of ball tensor salience of pixel. All the points with local maximum are as original candidate bifurcations. Finally, Principal Component Analysis (PCA) algorithm is utilized to eliminate non-bifurcations to get accurate bifurcations. To our best knowledge, there is no such application for tensor voting in this area. Experiment results of synthetic data and CT images of lung show that our method has better detection ratio, lower false detection ratio and better robustness than other vascular bifurcation detection methods.
Vascular bifurcation detection, Tensor voting, PCA algorithm
During pulmonary image analysis or clinical diagnosis and treatment, it is necessary to extract plenty of feature points as land-markers to compare body structure images obtained at different time in order to identify the disease. So, the research of feature point detection methods becomes a significant task. For a feature point of image, it is such point that uniquely represents the local feature of image, including corner, inflexion and bifurcation, and is robust to background and scalar of image. Feature point is so vital that it can be the cornerstone of such image technologies as image registration, image matching, object recognition, motion detection and image stitching. Additionally, it is applied to many medical fields as following: feature points can be an indicator of a separate vessel so that it is easy for doctors to track a specific vessel they need to observe during diagnosis of disease; feature point can identify a certain location as land-marker used for registration of multiple images so that they would be mapped to the same coordinate space; feature point has so good robustness to be used for object recognition. Therefore, feature point detection is favorable to diagnose disease and also a great important step for image subsequent processing.
For (Computed Tomography) CT images of lung, bifurcation is usually chosen as feature point because of its unique structure, which plays an important role in vascular localization in modern clinical diagnosis and image registration in image processing area. So, it is an important and challenge task to detect vascular bifurcation in lung image. However, it is heavy difficult to detect bifurcation as the low contrast and blurred vascular structure of lung CT image. So, there is less research on vessel bifurcation detection of lung image and there is no a unified standard about detection method. To our knowledge, vascular bifurcation detection can be classified into three categories as following:
(1) Bifurcation detection based on vessel central line extraction.
The flow of this kind method is that vessel structure is firstly extracted using vessel detection algorithm, thinning algorithm is used to extract skeleton of vessel for obtaining the single pixel vessel tree structure, and bifurcation is finally detected from the vessel tree. Zhang, et al. [1] utilized ZBS algorithm for vessel segmentation and Dijkstra algorithm for vessel center line extraction. This method has low accurate rate. Maduskar, et al. [2] used Frangi filter algorithm to extract vessel structure from lung image and Reebgraph algorithm to extract vessel center line. This method obtained lots of false positive bifurcations. Chen, et al. [3] analyzed the connection of logic tree structure extracted from thinned vessel to detect bifurcations. The bifurcations detected by this method is too concentrated.
(2) Bifurcation detection-based Hessian matrix
The flow of this kind of method is that a second order derivative matrix (Hessian matrix) of image is calculated to compute eigenvalues of the matrix, then a filter is constructed by the combination of eigenvalues and there is a maximum response at bifurcation. Zhou, et al. [4] proposed a new vessel filter to enhance vessel and bifurcation at the same time and finally detected the bifurcations by positioning the maximum response. But they did not make a distinction between bifurcations and non-bifurcations. Baboiu, et al. [5] presented a vascular bifurcation filter in scale space by analyzing eigenvalues of image. This method was just tested on synthesized data not the medical images. Nomura, et al. [6] built a detection function by Hessian matrix of vessel segmented by region-growing algorithm. This method mainly focuses on vascular nodules and pays not much attention to bifurcations.
(3) Bifurcation detection-based machine learning
This kind of method mainly uses machine learning algorithm to construct a classifier to train features extracted from image, and bifurcations are detected according to the classifier. Zhou, et al. [7] applied AdaBoost algorithm and the specific cross-sectional plane filter to vascular bifurcation detection. Zhao, et al. [8] extracted seven features to be the input of Random Forest classifier and designed a vascular bifurcation detector. However, this kind of method is comparatively time-consuming during training period as it adopts the machine learning algorithm.
In this paper, we propose a tensor voting based method for vascular bifurcation detection in CT image of lung. The purpose of this work is to detect vascular bifurcations accurately, which can be useful for the CT image analysis and processing of lung.
Two groups of data are used to test the effectiveness of my methods. One is synthesized vessel and the other one is CT image of lung.
1) First group: synthesized data
The synthesized data is a vessel structure included 5 bifurcations and 7 end-points in Figure 1a without noise.
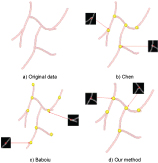 Figure 1: A comparison between bifurcation detection methods.
View Figure 1
Figure 1: A comparison between bifurcation detection methods.
View Figure 1
2) Second group: CT image of lung
The CT image of lung is from DIR-LAB [9] that provides a group of 4D CT images of lung consist of 10 cases, each one having a thoracic with six phases. As shown in Figure 2, we evaluate the validity of our method using four parts (PartA, PartB, PartC, PartD) segmented from the data at time 0 of first case (Case1_T00). Among the four parts of data, PartA and PartC are located at the edge of lung with small blood vessels, and PartB and PartD are located at the central of lung with large blood vessels, all of which are chose to demonstrate the effectiveness for different size of blood vessels.
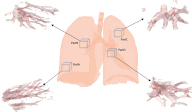 Figure 2: A comparison between bifurcation detection methods.
View Figure 2
Figure 2: A comparison between bifurcation detection methods.
View Figure 2
Tensor voting was firstly proposed by Guy [10] to solve feature extraction and segmentation of image and then was developed by Lee [11] and Tang [12]. In the past decades, tensor voting was successfully applied to many of issues in computer vision fields. In the paper, we present a tensor voting based vascular bifurcation detection according to the statistical property of the algorithm. The flow diagram of our method is shown in Figure 3.
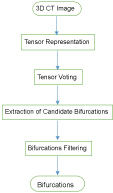 Figure 3: The overview of our method.
View Figure 3
Figure 3: The overview of our method.
View Figure 3
The image data is represented by a second order, nonnegative definite tensor, which encodes the salience of geometry (point, curve, or surface) of a pixel and its tangent or normal orientation together. The tensor T of image f is as following:
where are the second order derivative of a pixel at the directions of x, y and z respectively. is the second order derivative of a pixel at the directions of x and y. The rest of the other terms has the similar meaning. Additionally, a tensor is also a real symmetric matrix, which, in other way, can be decomposed into the combination of eigenvalues and eigenvectors. So, the other expression form of tensor is as following:
where are the eigenvalues of image, are corresponding eigenvectors. S, P, B are called as stick tensor, plate tensor and ball tensor respectively. For this kind of expression form of tensor, some cases are considered:
● If and , stick component is dominant, which means the pixel most likely belongs a surface with the normal direction .
● If and , plate component is dominant, which means the pixel most likely belongs a curve with the tangent direction and the normal plane spanned by and .
● If and , ball component is dominant, which means the pixel is most likely belong to a junction with no preference of orientation.
So, stick tensor, plate tensor and ball tensor represent the surface, curve and junction in coordinate space respectively and their weight factors, namely salience, represent the probability of the pixel belongs to a specific geometry in coordinate space.
After the image is encoded into tensor, then we describe the voting process, in which a vote is propagated from one pixel to another. The stick component is the most import in tensor voting algorithm and all other components are derived from it. The process of stick voting is as shown in Figure 4, in which V is a voter with the normal direction N, and R is a receiver of votes.
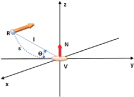 Figure 4: 3D Stick Voting.
View Figure 4
Figure 4: 3D Stick Voting.
View Figure 4
In Figure 4, s is the arc length VR, l is the distance between V and R, is the angle between y axis and the distance l. The osculating circle connecting V and R is the most likely connection as it keeps the curvature constant along the hypothesized circular arc. Then the most likely direction of vote cast from voter V to receiver R is normal to the circular arc at R (thick yellow arrow in Figure 4) and the vote, that is stick tensor, is as following:
Where is the salience decay function, determines the window size of voting , s and k have the following form:
According to [13], there is no vote cast from voter to receiver anymore if, so the algorithm just has one only parameter .
For the ball tensor from voter to receiver, it can be obtained by rotating stick tensor about y and z axes and integrating the contributions. So, it has the following form:
where is the rotation matrix that aligns stick tensor with the eigenvector corresponding to the maximum eigenvalue. are rotation angles about x, y, z axis respectively. has the following form:
According to the definition of ball tensor, it represents the junction in coordinate space. That is why we choose ball voting to detection vascular bifurcation in lung image. As shown in Figure 5a, the Y-shaped tubular structure is viewed as a 3D vessel. are three voters located at different branches of the vessel, and R is a receiver lactated at the bifurcation. The three dotted arrows represent three times voting and each voting process is shown in Figure 5b.
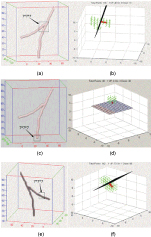 Figure 5: Bifurcations distinction by PCA.
View Figure 5
Figure 5: Bifurcations distinction by PCA.
View Figure 5
Finally, we extract vascular bifurcations according to the voting result. If the number of pixels of image is M, the number of the voting field is N, the accumulation of votes at each pixel can be written as follows:
can be also decomposed the following form:
where are eigenvalues of the tensor at receiver, are the eigenvectors corresponding to the eigenvalues respectively. Then, we calculate the local maximum value of (the salience of ball tensor) and find the corresponding pixels as the candidate bifurcations.
Due to the end-points of vessel also present strong salience of junction, the end-point may be selected by mistake as candidate bifurcations. Next, we demonstrate how to eliminate non-bifurcations using Principle Component Analysis (PCA).
Not all bifurcations extracted using ball tensor voting method are positive bifurcations. For example, some are end-points of vessel, others may be points located at middle of vessel. In order to eliminate non-bifurcations, we utilize PCA algorithm to filter candidate bifurcations.
Principle Component Anysis (PCA) was first proposed by Pearson, K [14]. The algorithm is mainly used to analyze data and build mathematical model. In this paper, we focus on the eigen-decomposition of covariance matrix and computation of principle direction, namely eigenvector corresponding to maximum eigenvalue. Then we apply the principle direction to distinguish bifurcation and non-bifurcation. The detail of this method is described as follows:
We choose one candidate bifurcation as a central point and construct a collection of coordinates using all points around the central point, N is the number of points in the selected space area. Then calculate the mean value coordinates and covariance matrix C, their forms are written as:
We calculate the eigenvalues and eigenvectors of the covariance matrix and choose the direction of eigenvector corresponding to maximum eigenvalues as principle direction. With the principle direction as normal direction, a plane going through the selected candidate bifurcation point is determined. Then count the number of points belong to the vessel, which are located above the plane, and the number , which are located below the plane. If or , the selected candidate bifurcation is an endpoint of vessel.
In the following part, we illustrate the effectiveness of our method on a synthesized Y-shaped vessel image. Three selected candidate bifurcations are located at bifurcation, end and middle of vessel respectively and PCA is performed to filter non-bifurcation in the three cases. The results are shown in Figure 5.
● If the candidate bifurcation is located at the bifurcation of vessel, the principle direction of point-set by PCA is shown in Figure 5b (the thick red line). With this direction as normal direction, the plane going through the candidate bifurcation is shown in Figure 5b (the black plane). Then we count the number of points located at each side of the plane respectively. If the number of points at one side is larger than the other side and both numbers are close to 0, the candidate bifurcation is identified as bifurcation of vessel.
● If the candidate bifurcation is located at the end of vessel, the principle direction of point-set by PCA is shown in Figure 5d (the thick red line). With this direction as normal direction, the plane going through the candidate bifurcation is shown in Figure 5d (the mesh grid plane). Then we count the number of points located at each side of the plane respectively. If the number of points at one side is larger than the other side and one of the numbers is close to 0, the candidate bifurcation is identified as an end-point of vessel.
If the candidate bifurcation is located at the middle of vessel, the principle direction of point-set by PCA is shown in Figure 5f (the thick red line). With this direction as normal direction, the plane going through the candidate bifurcation is shown in Figure 5f (the black plane). Then we count the number of points located at each side of the plane respectively. If the number of points at one side is most equal to the other side and none of the number is close to 0, the candidate bifurcation is identified as a middle point of vessel.
We use the two group of images to test our method and the results are compared with the methods of Chen [3] and Baboiu [5].
In order to describe the advantages and disadvantages of each method in quantitative analysis, we calculate the number of detected bifurcations, the number of no detectable bifurcations and the number of detected non-bifurcations. Then we evaluate the three methods by detection ratio (DR) and false detection ratio (FDR). DR is the percentage of the number of detected bifurcations and the actual number of bifurcations. FDR is the percentage of the number of detected non-bifurcations and the number of candidate bifurcations. Their forms are as following:
where true positives (TP) refers to the number of detected bifurcations that are actual bifurcations, false negatives (FN) refers to the number of no detectable bifurcations that are actual bifurcations, and false positives (FP) refers to the number of detected bifurcations that are not actual bifurcations.
In the first experiment, as shown in Figure 1, the method of Chen and mine can accurately detect 5 bifurcations, however, the method of Baboiu detects 5 bifurcations and 2 additional end-points and middle points of vessel. The FDR of method of us are 0% and DR are 100%, however, they are 50% and 80% for method of Baboiu respectively.
In the second experiment, the information of four parts data (show in Figure 2) is listed in Table 1. Figure 6, Figure 7, Figure 8 and Figure 9 show the results of bifurcation detection of three methods on the four parts of lung, which include 3D views (detected bifurcations are marked by yellow ball) and 2D views (bifurcation locations are marked by red x). Table 2, Table 3, Table 4 and Table 5 are the statistics on the number of detected bifurcations of three methods.
Table 1: The information of parts of lung. View Table 1
Table 2: The statistics on number of detected bifurcations on Part A data. View Table 2
Table 3: The statistics on number of detected bifurcations on Part B data. View Table 3
Table 4: The statistics on number of detected bifurcations on Part C data. View Table 4
Table 5: The statistics on number of detected bifurcations on Part D data. View Table 5
In Figure 1, we can see that the method of Chen is obviously better than Baboiu. That is because the structure of the synthesized vessel is so clear that an ideal thinned vessel tree can be obtained without vessel segmentation of the original data.
In Figure 6, Figure 7, Figure 8 and Figure 9, the bifurcations detected by the method of Chen is relatively concentrative because low contrast image results in the imperfect segmentation of vessel structure, which further influenced the thinning result of vessel and then bifurcation detection. The bifurcations detected by Baboiu method are dispersed at the edge of image as noise affects the reliability of eigenvalues decomposed from hessian matrix of image. Table 2, Table 3, Table 4 and Table 5 also show that the methods of Chen and Baboiu have a high false detection ratio and low detection ratio, however, our method has low false detection ration and high detection ratio. All the experiment results verify the effectiveness and robustness of our method.
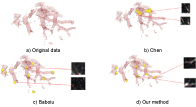 Figure 6: Bifurcations detected by three methods on Part A data.
View Figure 6
Figure 6: Bifurcations detected by three methods on Part A data.
View Figure 6
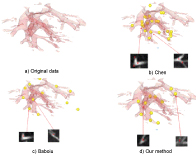 Figure 7: Bifurcations detected by three methods on Part B data.
View Figure 7
Figure 7: Bifurcations detected by three methods on Part B data.
View Figure 7
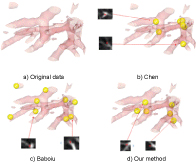 Figure 8: Bifurcations detected by three methods on Part C data.
View Figure 8
Figure 8: Bifurcations detected by three methods on Part C data.
View Figure 8
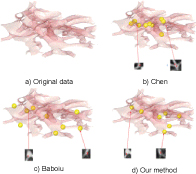 Figure 9: Bifurcations detected by three methods on Part D data.
View Figure 9
Figure 9: Bifurcations detected by three methods on Part D data.
View Figure 9
However, there are tremendous add operation of pixels for tensor voting algorithm, so we just test our method on parts of whole lung image. In the future, we might apply the method to the whole CT image of lung accelerated by graphic processing unit (GPU) to verify the effectiveness and robustness.
This research is partially supported by the Shenzhen Fundamental Research Program (JCYJ 20170818100006280).