The effect of the applied RF field in an NMR experiment on the magnitude of the Spectral Density for a Dipolar Relaxation Mechanism is demonstrated theoretically. The effect is shown with Sin Cos Pulse as a concrete example. The order of magnitude of the magnetic moment where these effects will be significant for typical Rf amplitude values is derived. The effect may be of utility in providing an alternate method of control for MRI Tissue Contrast applications with further development.
In contemporary NMR methodologies, it is common to find experimental scenarios where the relaxation of the magnetization during a pulse train is important to be able to model and quantify [1-3]. In this note we suggest that for some molecular species the Rotational Diffusion can be affected and modified by the Magnetic Field Torque of the applied radio-frequency pulse. During the course of working on this concept, it has come to our attention that the Russian investigator Sitnitsky [4] has investigated this phenomenon.
This proposed influence may be important in some models for explaining experimental data, such as for Liquid Crystals [5]. We demonstrate the derivation of this effect on the spectral densities following the classic treatment of Abragam [6] and gives some ranges of parameters where this effect may be of importance.
We note that the proposed effects may be useful as another avenue to control the spin dynamics of an experimental system while the pulse is on. Also, the proposed effects have been dealt with rigorously in the Physics Literature [7].
The "Toy Model" we propose to explicate this effect is the following.
We envision a spin system, transformed to the so called Tilted Doubly Rotating Frame (TDRF [8]). In this frame there will be defined a so-called "effective field." We can write down an effective Hamiltonian for the applied RF of the following form:
For the exposition here we consider the Sin/Cos pulse, defined as:
Where is a constant (See for example the relevant papers of the Garwood Group [9-11].
In the TDRF the effective field can be seen from geometric arguments to be defined as:
Substituting Eq [2 a,b] into Eq[3], one easily appreciates that . So that as required for our argument the effective field defined as:
Where is the particle gyromagnetic ratio.
Now we consider a Molecular Species in solution with a defined dipole moment .
In a constant field , there is a potential energy of interaction [12] between the moment and the field defined as:
Here the angle is defined as the angle between the vectoral directions of the dipole moment and the constant field.
We change to the convenient notation:
So that:
Knowing the geometry between the effective field and the magnetic moment in the TDRF, it is Seen that the angle is defined as:
Using Eq [2a,b] in Eq [7] we see that:
Suppose we take the Nuclear Species of Interest to be in a molecule that we model and approximate as a sphere. We assume that the Rotational Brownian Motion can be represented as a series of small incremental rotations. We seek to find the Correlation Function which characterizes the rotational diffusion. As treated, in for example Abragam Chapter VIII or other places in the literature [13,14] we can define the Correlation Function in terms of the spatial part of the Dipolar Interaction Hamiltonian. If we adopt the notation of Abragam, we can define the Correlation Function as:
Where we set and consider the case where is zero.
So, to carry out this program we need to an expression for the Probability Density Function.
This PDF will be a solution of the so-called Smoluchowski Equation (SE), where the effects of the applied RF Torque will be included. As one can infer there are numerous assumptions one can apply to the formulation of the SE. The solution in general, (see for example the classic papers of Coffey's group [12] are not totally trivial, usually the derivation of series solutions which involve the solution of iterative expressions for the expansion coefficients, or continued fraction solutions.
We have chosen to present and use the solution of Sitnitsky [4] which is the most easily implemented solution we have found to program for demonstration of our methods.
Please see Appendix I for a detailed definition of the terms in the series expression for the PDF.
The PDF can be taken to be the approximate solution of the following partial differential Equation using our expression for the Potential Energy Term [4].
Here b is a constant defined in (4).
In Eq [10] x is defined to be as where measure as defined previously the interaction between the Moment and the RF field with the definition:
We can use the definition of the PDF to compute the Correlation Function as In Eq [9] and then compute the corresponding Spectral Density as:
In Figure 1 we show the dependence of the Spectral Density as given in Eq [12], for the case mp = 0.
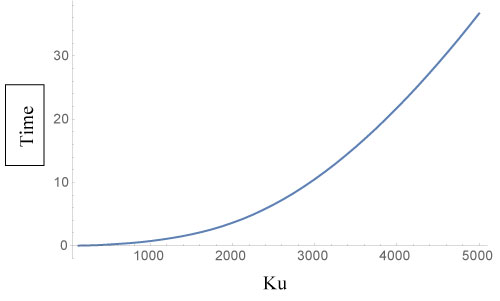 Figure 1: Dependence of Spectral Density on the Ku parameter. (See text for definition of Ku).
View Figure 1
Figure 1: Dependence of Spectral Density on the Ku parameter. (See text for definition of Ku).
View Figure 1
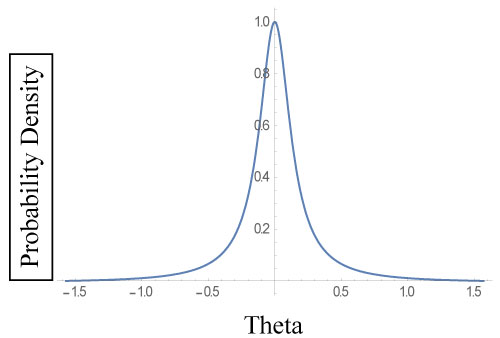 Figure 2: Plot of Probability Density Function Theta.
View Figure 2
Figure 2: Plot of Probability Density Function Theta.
View Figure 2
As can be seen there is found to be an appreciable dependence of the Spectral Density on the parameter This is taken to indicate that the RF Field, with a range of values which will be discussed below, can affect the Spectral Density which is used to compute relaxation functions [6,13-15]. So that the RF field, through interaction on the Rotational Brownian Motion, can influence the values of the calculated relaxation functions during a pulse sequence.
To the knowledge of the author, this possibility has not been fully appreciated in the NMR literature.
The reader may wonder what is a lower bound on the magnetic moment of the particle of Interest for a typical value of the pulse amplitude.
In the Garwood papers [9-11], the pulse amplitude is typically on the order of Hz. Then we reason that the interaction energy of the magnetic moment with the field in the TDRF should be greater than the thermal energy of the surrounding liquid medium.
So, we propose:
Or
We note that the units of a magnetic moment can be seen in CGS units to be .
So, at room temperature in CGS units, is on the order of .
, is typically on the order of Gauss.
Practical lower bound on the magnetic moment of the particle for an effect of the RF field on the Rotational Brownian Motion of the particle and consequently on the Spectral Density for a dipolar relaxation mechanism.