Objectives: In this paper, single and multiobjective optimal control is performed on a Corona Virus disease model involving hospitalizations and non-pharmaceutical intervention tasks to minimize the damage done by the virus. This model considers the effects of hospitalization and non-pharmaceutical interventions like quarantining and social distancing.
Methods: This method does not use weighted functions but minimizes the distance from the utopia point. The utopia point is obtained by the single objective optimal control procedure and the multiobjective optimal control is performed by minimizing the distance from the Utopia point. The optimization program, Pyomo where the differential equations are automatically converted to a Nonlinear Program is used in conjunction with the state-of-the-art global optimization solver BARON.
Results: Four single objective optimal control and one multiobjective optimal control problem were solved. The single optimal control involves minimizing the infections, death rate, and the cost of performing the control tasks and maximizing the recovered subjects. The multiobjective optimization involves minimizing the infections, death rate, and the cost of performing the control tasks and maximizing the recovered subjects at the same time. It is observed that the multiobjective optimal control is as effective as the single objective optimization in addition to having the advantage of controlling many variables.
Conclusions: The multiobjective optimization involving the minimization of the distance from the Utopia point is very effective to obtain the best control profiles and enables one to maximize the number of recovered subjects while keeping the cost of performing the control tasks as low as possible. In fact, it is as effective as the single objective optimal control that involves maximizing the recovered subjects without dealing with the cost of performing the control tasks.
The number of fatalities caused by the Corona Virus disease (COVID) virus is not only extremely high but also increasing at an alarming rate. The many strategies that are being used throughout the world, to control the pandemic, are being overwhelmed mercilessly by the global pandemic. The exponential increase in the number of confirmed infectious cases and deaths has caused countries all around the world to respond with severe lock-down, quarantining, and social distancing measures to contain the spread of the disease. It is causing so much suffering that one must do whatever possible to minimize the damage until a cure or/and a reliable vaccine is developed. The rapid spreading of this virus and the amount of fatalities has led to a lot of research in the year 2020 alone developing strategies to minimize the damage [1-23]; An interesting article [17] deals with optimal control of the covid pandemic model with hospitalization and non-pharmaceutical interventions. However, in this work a single function was minimized subject to the differential equations that govern the COVID model. This paper deals with the use of rigorous multiobjective optimal control (MOOC) for the same Covid pandemic model involving hospitalization and non-pharmaceutical interventions [17]. It is demonstrated that multiobjective optimal control procedure will yield very similar results (in addition to controlling the other variables) for the important variable that represents the number of recovered subjects as when a single objective optimal control is performed maximizing this variable.
In the model [17], the outside infections affect the susceptible population S at a rate . This results in the formation of an exposed group E. This group has a life span of days. The symptomatic infected subjects, I, would be a portion of the exposed group. The remaining subjects, A, are classified as asymptomatically infected and constitute a fraction of the symptomatically affected.
The set A has a life span of days. All asymptotically infected subjects and a fraction of the infected subjects recover and become immune. A fraction of the symptomatically infected subjects become a hospitalized group and they either recover or perish. The equations that govern this model are
(1)
(2)
(3)
(4)
(5)
(6)
The number of deaths is a function of the hospitalized subjects and is given by
This formulation accounts for the situation where the existing hospital resources (like hospital beds) are not adequate to ensure that all the hospitalized patients are taken care of. The Variable names are given in Table 1 and the parameter values are given in Table 2. All the data values are taken from Perkins and Espana [17].
Table 1: The Variable names. View Table 1
Table 2: Parameter values. View Table 2
In the multiobjective nonlinear optimal control (MOOC) strategy [24,25] used in this work the single objective optimal control problem is first solved for each of the objective functions. This procedure does not involve the use of weighting functions not does it impose additional parameters or additional constraints on the problem unlike the weighted function or the epsilon correction method [26].
For a multiobjective optimal control problem
the single objective optimization problems are solved independently minimizing each (i = 1,2,3…n) individually. This will lead to minimized values
(i = 1,2,3,..n). Then the problem that will be solved is
The optimization program, Pyomo [27] where the differential equations are automatically converted to a Nonlinear Program (NLP) using the orthogonal collocation method [28] is used for performing the dynamic optimization calculations. The Lagrange-Radau quadrature with three collocation points and 10 finite elements are chosen. The resulting nonlinear optimization problem was solved using the solver BARON 19.3 [29] accessed through the Pyomo-GAMS27.2 [30] interface. BARON implements a Branch-and-reduce strategy and provides a guaranteed global optimal solution.
Four single objective optimal control and one multiobjective optimal control problems are solved. Figure 1 (a-f), Figure 2 (a-f), Figure 3 (a-f), Figure 4 (a-f) and Figure 5 (a-f) represent the profiles of S, I, H, D, (H-D), U for each of these optimal control problems. The time considered is 1 year (365 days). In the first problem the total number of infected persons, I, is minimized. The best individual solution obtained by Baron is zero and that is considered to be the Utopia point. In the second optimal control problem the number of deaths, D, is minimized and the utopia point obtained is 4.274 × 10-5. In the third problem, (H-D) the number of recovered patients is maximized and the resulting utopia point is 0.1132. In the fourth single objective optimal control tasks are minimized to keep the price as low as possible and the utopia point is 0 again. In the multiobjective problem the objective function that is minimized will be
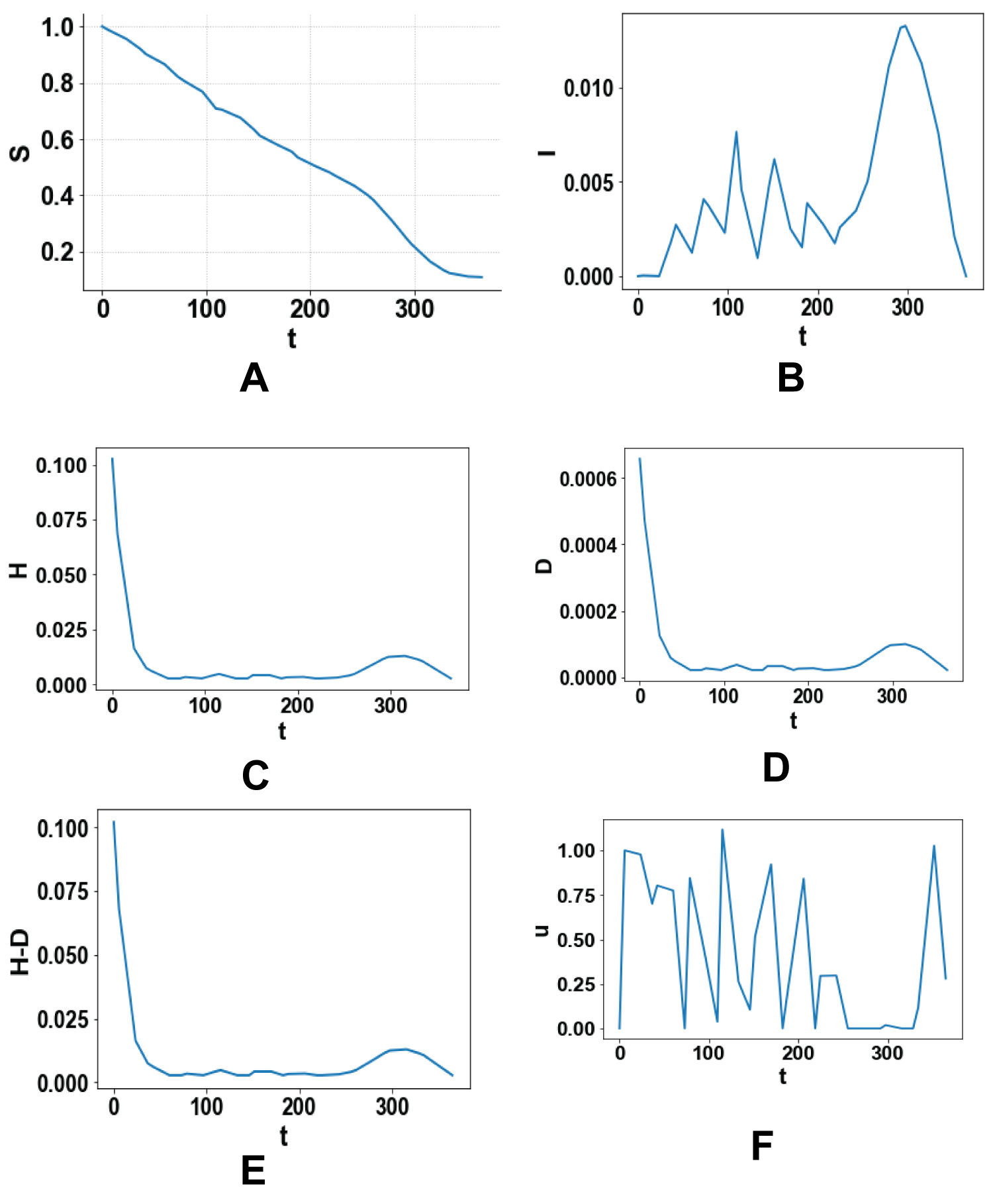 Figures 1: (a-f) Optimal control minimizing the total number of infected persons, I.
View Figure 1
Figures 1: (a-f) Optimal control minimizing the total number of infected persons, I.
View Figure 1
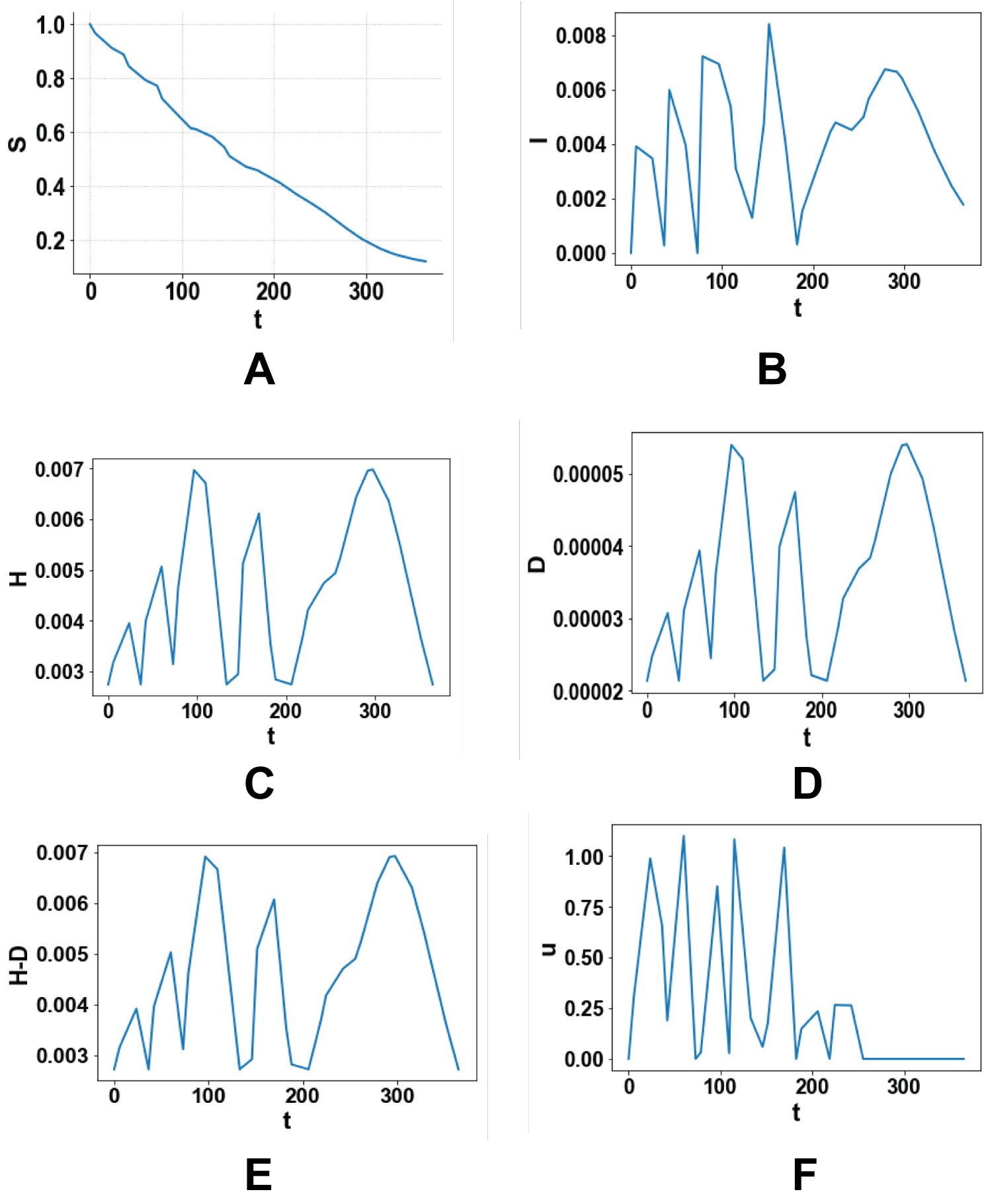 Figure 2: (a-f) Optimal control minimizing the total number of deaths D.
View Figure 2
Figure 2: (a-f) Optimal control minimizing the total number of deaths D.
View Figure 2
 Figures 3: (a-f) Maximizing the number of people recovered after hospitalization H-D.
View Figure 3
Figures 3: (a-f) Maximizing the number of people recovered after hospitalization H-D.
View Figure 3
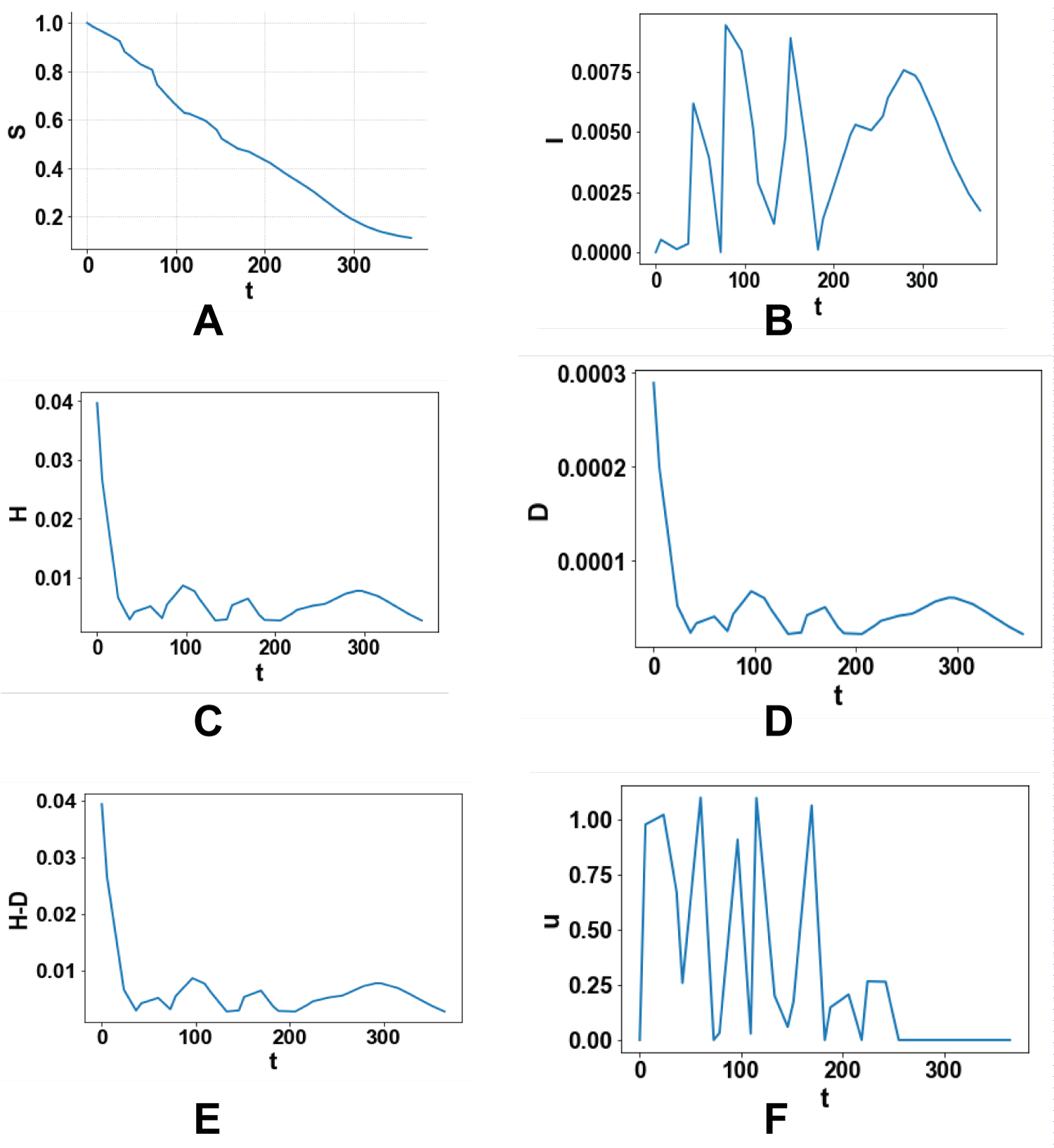 Figure 4: (a-f) Minimizing the control actions to keep the expenses as low as p.
View Figure 4
Figure 4: (a-f) Minimizing the control actions to keep the expenses as low as p.
View Figure 4
 Figure 5: (a-f) Multiobjective optimal control profiles.
View Figure 5
Figure 5: (a-f) Multiobjective optimal control profiles.
View Figure 5
This kind of multiobjective optimal control is very effective as it considers all the factors in a single optimal control task and enables the most effective strategies to be used. A comparison of Figure 3e and Figure 5e involving the most important variable (H-D), demonstrates that the multiobjective optimal control almost captures the same profile as the single optimal control solely maximizing the same variable while controlling the other variables as well. This demonstrates that this procedure is not only rigorous but also more useful than single objective optimizations as it allows for the control of more than one variable while being as effective.
A rigorous multiobjective optimization procedure is used for the Covid model that involves hospitalizations and non-pharmaceutical interventions. It is demonstrated that this strategy is effective as it produces almost the same profile for the number of recovered subjects as when a single objective optimal control is performed maximizing the same variable, while controlling the other variables at the same time. The future work will involve the performance of such a multiobjective optimal control for other covid models.
The author has no conflict of interest.