Personalized medicine today is primarily addressing efficacy. Here we investigate and illustrate the role that precision medicine could play in drug safety by supporting the identification of subjects at high risk of harm by an otherwise safe and efficacious treatment. Predicting potential harm requires high sensitivity of a classification rule. After reviewing some case studies from the literature we discuss the appropriateness of two methods to identify sub-groups of patients at risk. To illustrate the methods we reanalyze one of the examples and provide performance results of the methods by simulations. It turns out that basing a predictor of the most appropriate treatment on the individual treatment estimator can achieve results superior to those obtained from within-subgroup significance tests when sensitivity and relevance are the main concerns. In conclusion, significance tests should not be the first choice approach to identify subgroups of subjects at risk of harm of an otherwise safe intervention.
Personalized medicine, Drug safety, Biomarker, Covariates, Harm prevention, Individual treatment effect
Personalized or precision medicine is established in oncology and starts to become adopted in other therapeutic areas as well. Drug regulators have bought into the concept such that a good number of newly developed drugs obtained approval only for a subgroup of patients identifiable by a specific biomarker (see for example) [1].
As it stands, personalized medicine currently focuses primarily on efficacy, i.e., on the identification of subgroups of patients that respond better to an intervention than others. In the following we consider the situation where an efficacious treatment is tolerable for the majority of subjects but can cause unacceptable harm to a subgroup. In case this subgroup could be identified and individuals could be classified accordingly, the drug could be safely administered by applying it only to subjects not at risk of harm.
To give an idea of the type of harm we have in mind we use natalizumab in multiple sclerosis as an example [2]. This drug, an immunosuppressant, increases the risk of a rare brain infection called Progressive Multifocal Leukoencephalopathy (PML) that usually leads to death or severe disability [3]. There is no known biomarker by which one could separate patients at high or low risk of PML other than a John Cunningham Virus (JCV) infection which also increases the PML risk. Because the PML risk increases over time of exposure, treatment with natalizumab has to be stopped after 2 years. The medication is only accessible through a restricted distribution program [4].
The decision to administer a drug only to a subgroup of patients instead of the broader population bears the risk to withhold an efficacious treatment from a subgroup. Not personalizing the drug use for efficacy reasons when it should be done risks to offer a subgroup of patients a non-efficacious treatment. If safety is a concern for a subgroup, one would offer a harmful drug to this subgroup if the drug would be given to all patients. Therefore the balance between false-positive and false-negative predictions is different when personalized medicine is concerned with efficacy or safety. In the latter case, preventing harm may have priority to the extent that it is desirable to identify individuals from the susceptible group at the expense of falsely identifying some not belonging to it. In other words because the utility of predictive safety markers is to exclude patients at risk of harm, sensitivity is of greatest importance.
We present three examples from the literature that are concerned with finding subgroups of patients at high risk of unwanted effects, mainly to illustrate what has been done in this regard in the past. Then mainly two methods to identify subgroups will be described briefly, one based on significance tests and one on the Individual Treatment Effect (ITE) which is defined as the expected effect in an individual characterized by specific covariates. These considerations are then applied to the first of the three examples and contrasted with the results of the publication. In a small simulation study the performance of the methods will be investigated. Finally some conclusions are drawn on the applicability of subgroup selection in the context of drug safety.
Contrast-Induced Nephropathy (CIN) is a serious complication of diagnostic and interventional procedures. In [5] the risk of nephrotoxicity was compared under two contrast media, Isosmolar Iodixanol (IOCM) and a Low-Osmolar Medium (LOCM). Furthermore the authors set out to identify predictors of contrast induced nephropathy. An individual patient data meta-analysis including 2727 patients from 16 double-blind, randomized, controlled trials with stratification according to Chronic Kidney Disease (CKD) and Diabetes Mellitus (DM) was performed. Endpoints were increase in serum Creatinine (Cr) and incidence of post-procedural contrast-induced nephropathy, defined as a rise of creatinine by more than 0.5 mg/dl. The CIN rates by subgroups are shown in Table 1. The authors conclude that "Patient-related predictors of CIN were found to be CKD and CKD + DM, but not DM alone". We get back to this conclusion in Section 4.
Table 1: Number of patients with CIN over total number of patients by patient subgroups and contrast media from [5]. View Table 1
Even after approval of recombinant tissue plasminogen activator for acute ischemic stroke concerns remained about the risk of bleedings. To analyze whether special subgroups of patients have a higher risk of Symptomatic Intracerebral Hemorrhage (SICH), the results of 4 prospective observational studies including 1966 acute stroke patients treated within 3 hours with alteplase have been analyzed [6]. No (numerical) SICH rates by subgroup are presented in the paper but a forest plot depicting the incidences of SICH for each subgroup. Surprisingly, the SICH rate of 6.4% from the National Institute of Neurological Disorders and Stroke (NINDS) study [7] is used as reference instead of the one obtained from the 4 studies which are 4.7% with a 95% confidence interval of 3.8-5.9%. The paper concludes: "There was no statistically significant increase in the SICH rate in any of the five specified subgroups of patients (advanced age, NIHSS > 20, Hispanic ethnicity, diabetes and CHF)".
Concerns over hepatoxicity have contributed to the withdrawal or non-approval of lumiracoxib which is efficacious in osteoarthritis and acute pain. To identify genetic markers able to select individuals at risk for developing drug induced liver injury a case-control genome - wide association study was conducted in 41 lumiracoxib treated patients with liver enzyme elevations above 5 times Upper Limit of Normal (ULN) and 176 patients without liver injury [8] using DNA samples collected from the TARGET study [9]. Endpoints were time to liver enzyme elevations above 5 times ULN. Fine mapping identified a strong association to a common HLA haplotype. HLA-DQA1*0102 had the best results in terms of negative predictive value (99%) and sensitivity (73.6%).
To further examine the performance characteristics of the marker, all remaining 4518 lumiracoxib treated patients from the TARGET study with DNA available who had given informed consent were genotyped for presence or absence of HLA-DQA1*0102. Kaplan-Meier (KM) estimates of the cumulative incidence of liver enzyme elevations were obtained for HLA-DQA1*0102 carriers and non-carriers and compared to estimates for all patients treated with lumiracoxib, ibuprofen or naproxen. As it turns out, the KM curve for lumiracoxib treated subjects who are DQA*0102 carriers is increasing much faster over time than the KMs for patients treated with the comparator drugs. The risk of non-carriers under lumiracoxib is similar to the risk in the overall population under the comparator treatments (Figure 1 in [8]). The paper concludes: "The results presented here provide strong evidence that the HLA-DQA1*0102 allele would have clinical utility as a screening marker to exclude carriers from lumiracoxib treatment".
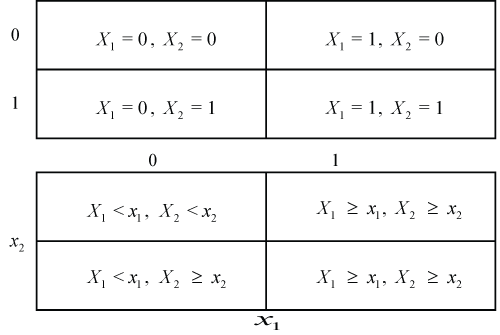 Figure 1: Subgroups defined by the individual treatment effect in the case of two binary (upper diagram) or two numerical covariates (lower diagram). In either case only two subgroups are obtained.
View Figure 1
Figure 1: Subgroups defined by the individual treatment effect in the case of two binary (upper diagram) or two numerical covariates (lower diagram). In either case only two subgroups are obtained.
View Figure 1
The most intuitive way to account for subgroups when analyzing clinical trials is to identify covariates potentially predictive for a treatment effect. If these variables are binary (like gender) they define two subsets of subjects. If they are continuous (like age), subsets can be obtained by defining a threshold and assigning all subjects with values above the threshold to one subset and the rest to the other subset. Subgroups can then be formed by intersections of the subsets generated by covariates as shown for two covariates X1 and X2 in Figure 1 (see [10] for an overview). There are basically two ways to identify subgroups: First, to consider the treatment effect within each subgroup or to consider the excess effect in one subgroup relative to the effect in a reference subgroup, i.e., treatment by subgroup interactions. The first analysis can be done on the raw data from each subgroup while the second may require modeling to define interactions.
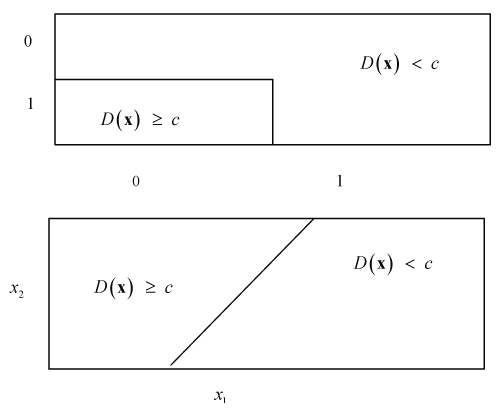 Figure 2: Subgroups defined by two binary (upper diagram) or two numerical covariates X1 and X2 with corresponding thresholds x1 and x2 (lower diagram).
View Figure 2
Figure 2: Subgroups defined by two binary (upper diagram) or two numerical covariates X1 and X2 with corresponding thresholds x1 and x2 (lower diagram).
View Figure 2
Some authors prefer to consider interactions to identify subgroups over within subgroup comparisons [11,12]. However, they also acknowledge that interaction tests can suffer from lack of sensitivity. For this reason, interaction based methods may not be appropriate for safety analyses and will not be considered further.
Another way to define subgroups utilizes the Individual Treatment Effect (ITE) which is defined as follows: For controlled studies, let be the outcome of a subject with covariates under intervention . The individual treatment effect [13, 14] is defined by
for some link function g (see [15]). Examples are
• for normal/log-normal outcomes (e.g., lab values)
•
for binary data (e.g., occurrence of adverse events)
Given the appropriate ITE one can set a threshold c to obtain a corresponding subgroup
An example for two covariates is shown in Figure 2. The threshold c reflects a clinically relevant effect to be defined by clinicians, regulators or policy makers.
The aim of both approaches is to identify subgroups based on a classification rule. The first method uses significance tests to achieve this goal; the second method does not consider significance at all but relevance of an expected effect, in our case a potentially severe side effect. The two options of defining subgroups have advantages and disadvantages. The marginal thresholds used under the first approach are easy to interpret and the subgroups are defined in a straightforward manner based on the original data. Considering treatment effects within subgroups does not require data modeling. However, the approach can generate very large numbers of subgroups even for moderate numbers of covariates. It requires dichotomization of otherwise continuous covariates which can become problematic. If interactions rather than direct effects in subgroups are to be considered, modeling may be required. Basing decisions on tests for differences within groups or interactions emphasizes statistical significance rather than relevance.
The approach using the ITE defines subgroups in terms of relevant expected outcomes rather than covariate related thresholds. It divides the covariance space in two subsets regardless of the number of covariates. However it may require modeling and lead to rather unintuitive relationships between effects and covariates.
To illustrate the two concepts of subgrouping we reanalyze the CIN rate data from [5] presented in Table 1. Though the data stem from 16 randomized trials, only summary data are reported in the paper.
For our analysis we fitted a saturated logistic model to the data. Let X1, X2 denote the indicator variables for CKD and DM, respectively, let Z denote the treatment indicator with Z = 0 coding for IOCM Z = 1 for LOCM. Let be the probability of CIN in a patient with covariates treated with . Then
The prognostic effects describe the dependence of the response under treatment Z = 0 while the predictive effects account for the additional impact of the covariates under Z = 1.
We fitted model (1) to the learning data set in Table 1 and obtained the results in Table 2. The odds ratios and confidence intervals are identical to those in Table 3 of [5], however, the p-values differ since we took the results of the asymptotic tests from the logistic model rather than from Fisher's exact test as was done in [5]. Nevertheless, the results are practically identical since the corresponding comparisons result in either very small or large p-values. Note that the comparison of patients with and without diabetes was not done in [5], though the authors explicitly excluded DM from being predictive on its own.
Table 2: Odds ratios of the risk of CIN under contrast medium 1 relative to medium 0, Odds ratios and confidence intervals are identical to those in Table 4 of [5], p-values differ from those of Fisher's exact test which are presented in the paper. View Table 2
Table 3: Simulation scenarios: is the number of subjects per treatment and OR(x) the odds ratio of the risk of harm under treatment 1 over treatment 0 for subjects with covariates . Independently of x. Scenario 2 differs only with respect to instead of 100 from scenario 1. View Table 3
The ITE corresponding to model (1) is given by
Note that the ITE does not depend on prognostic effects and that
is the odds ratio of the probability to experience CIN under medium 1 relative to medium 0 for a subject with covariates x. Let , and be the Maximum Likelihood (ML) estimators of , and , respectively, then
is the ML estimator of D(x). A predictor for the most appropriate treatment of a future patient with covariates
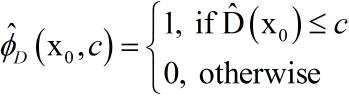
For the CIN data we decide that medium 1 should be preferred over medium 0 when the observed reduction of CIN risk is 50% or more. In other words, medium 0 should not be given to subjects when the CIN risk over medium 1 more than doubles relative to medium 1. A predictor for the best treatment is therefore given by . This rule should be reasonable since the overall CIN risks are 3.5% for medium 0 and 1.4% for medium 1. According to this decision rule, all subjects with DM or CKD or both should be given contrast medium 1.
The decision rule in the ITE based method depends solely on the point estimates of the odds ratios. One wonders how stable such a predictor is or whether it can be improved to reduce prediction error. Bagging (or bootstrap aggregating) predictors is a method for generating multiple versions of a predictor and aggregate them in the hope to obtain a better predictor. The aggregation averages over the versions when predicting a numerical outcome and does a plurality vote when predicting a class. The multiple versions are formed by bootstrap replicates of the original dataset. If perturbing the data set can cause significant changes in the predictor constructed, then bagging can improve accuracy [16].
In our case let be the number of subjects with Z = z and X = x in the database and let n(z, x) be the number of those subjects with CIN. For b = 1,...,B, we draw new random numbers from a binomial distribution with parameters and and obtain the corresponding ITE estimates . Then let
Where denotes the indicator function. is an estimator of the probability that a future subject with covariates x0 will be assigned medium 1 correctly given the data from the learning set. A predictor of the most appropriate treatment for the subject is
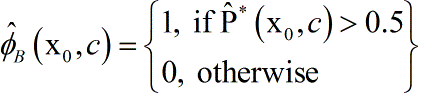
i.e., the medium the majority of the bootstrap samples are voting for. For the example the predicted treatment is given by . Besides serving as a predictor of the most appropriate treatment, is also a measure of prediction accuracy.
In the example, the results from bagging confirm the results from the decision rule based on the point estimates (see Table 4). This outcome is contradicting the conclusion of the original paper [5] which stated that only CKD and CKD + DM are predictors of CIN but not DM alone.
Table 4: Predicted odds ratio and proportions of B = 1000 bootstrap samples leading to a preference of contrast medium 1 for a future subject with covariates . View Table 4
To illustrate that bagging will not always support the decision derived from the point estimate assume that instead of 3 just 2 out of 158 subjects with DM alone would have experienced CIN. This would result in an odds ratio of 0.44 which is less than 0.5 for the CIN risk of medium 1 vs. medium 0, but bagging would provide .
We compare the operating characteristics of the subgroup selection method based on statistical tests within subgroups with that based on a bagged ITE. To this end a simulation study will be performed. Treatment 0 is assumed to have the same effect on subjects in all subgroups, namely . The odds ratios of harm differ for the other subgroups according to the forth column of Table 3. We assume a 10% significance level for test for difference within subgroups. Treatment 1 must not be administered to subjects with a predicted 20% or higher increase of the odds ratio relative to treatment 0, i.e., if . We refrained from using 1 as a threshold since otherwise the probability to detect an alarming situation if the effects of the treatments are equal would be 50%. The simulation results are shown in Table 5.
Table 5: Proportion of 5000 simulations with B = 1000 bootstrap draws for each simulation where future subjects with covariates x0 are denied treatment 1 for a significant difference within subgroups (column 3), an ITE estimator greater than c (column 4) or a probability of at least 0.5 for the ITE estimator to be greater than c (column 5) with c = log (1.2). The last row shows the results for a prediction model that is derived from 1000 subjects per treatment with x1= x2 = 0 instead of 100 while all the other settings remain unchanged. View Table 5
As expected if subgroups are determined based on significance tests, one controls the false positive rate, but the detection rate is low. This leads to a probability of a correct decision of more than 90% in the subgroup defined by . However, this probability is less than 32% in all other subgroups allowing administering a drug that can be harmful with an unacceptably high probability.
The probability of a correct decision is much higher for the ITE based method for the subgroups with at the expense of declaring a greater number of patients falsely to be at risk. Prediction correctness improves when the number of patient data used to create the predictor increases. This is shown for the marker negative subgroup in the last row of Table 5.
It can also be seen from Table 5 that a prediction of the best treatment based on the bagged predictor changes the probability of a correct decision only marginally. This suggests at least for the specific simulation that the predictor derived from the point estimate is fairly stable. The value of bagging in this case is discussed in Section 6.
The main motivation for this investigation was to extend the concept of personalized medicine to safety aspects of interventions. Instead of asking the question which subjects experience high efficacy one is concerned about which subjects should not be given a treatment because of a high risk of harm. Examples from the literature have been presented some of which leave some open questions. The first one [5] does not report all analyses when drawing conclusions and may therefore have overlooked the impact of diabetes alone. The second [6] is not comparing subgroup results with overall results from the same set of studies but from an external one with a higher overall SICH rate. Could this alter the conclusions of the study, in particular the relevance of diabetes for the occurrence of SICH? The most comprehensive and understandable report of a safety related subgroup analysis is provided by the third example. The latter is selecting the marker by maximizing sensitivity and negative predictive value, not by considering tests and p-values.
One dataset has been discussed in some detail to point to the shortcomings of using significance tests within subgroups to define subgroups. Instead, a method based on the individual treatment effect is proposed that has some advantages over the testing approach. First, it is based on a relevant effect difference. This allows defining what is considered too high a risk. This is not directly possible with significance tests which control the false positive rate but not the power or sensitivity. In fact, as was said earlier, the main requirements for a method supposed to identify subjects at risk are high sensitivity. In this regard the new proposal is superior at the expense of a somewhat higher false positive rate. This could result in withholding an otherwise safe and efficacious treatment from many subjects who could benefit. However, the false-positive rate could be reduced by increasing the sample size in the subgroup of the learning data where no harm is expected. This should be the largest patient group if the treatment is well tolerated for the majority of patients.
When bagging cannot reduce the prediction error, one would be inclined to follow the advice in [16] not to do it at all. However, provides information about the probability that a future subject with x0 will be assigned correctly to the best treatment by considering sampling variability in the learning dataset of the predictor. In other words it provides a measure of prediction accuracy or uncertainty. To be on the safe side, we have used substantially more bootstrap samples than the 25 recommended being sufficient in [16] since this number has been derived for situations where bagging improves prediction. The guiding principle we followed was to increase B until the results start stabilizing.
The example considered in more detail was one with two binary covariates which define four subgroups and a binary outcome (CIN). However, the approach works for continuous outcomes and covariates as well. The method also works for single arm studies like the alteplase trial. For this let be the outcome of a subject with covariates x and set
An issue can arise when the number of covariates becomes large, for example in a genetic study. In this situation the prediction accuracy of the ITE will decrease because the prediction model contains many variables contributing mainly noise but no information. Too many covariates are also not helpful in interpreting results. Thus variable selection methods should be included in the model fitting process requiring methods of selective inference for the analysis (see [17]).
Another important question to be addressed is whether subgroup findings require confirmation in some sense. For efficacy an analysis concluded that corroboration is often not taking place and if so, results are only confirmed exceptionally [18]. Eventually, one could consider efficacy and safety together and consider prediction of the most appropriate treatment under a benefit risk perspective.
This work has been funded by the FP7-HEALTH-2013-INNOVATION-1 project Advances in Small Trials Design for Regulatory Innovation and Excellence (ASTERIX). Grant Agreement No. 603160. Website: http://www.asterix-fp7.eu and by the UK Medical Research Council, Project No. MR/M005755/1.