For a rare disease, all the patients having the disease constitute a small population, and the standard single-stage hypergeometric test is uniformly most powerful to evaluate the response probability of a specific treatment regimen. Although exact group sequential designs are widely employed in phase II clinical trials for binomial proportions, it is unknown whether or not similar tests can be employed for hypergeometric proportions. In this manuscript, it is proved that, for hypergeometric proportions, there exist exact group sequential designs that achieve the predesignated significance level and power with maximum total sample size bounded above by the sample size for the corresponding standard exact single-stage test. Additionally, two types of optimal two-stage designs are examined for a range of design parameters; one is optimal in the sense that the expected sample size under the null hypothesis is minimized, and the other is optimal in the sense that the maximum sample size is minimized.
Exact group sequential designs, Hypergeometric distribution, Minimax designs, Optimal designs, Small population, Uniformly most powerful test
For a rare disease, all the patients having the disease constitute a small population of size N. Phase II trials of Investigational New Drugs (INDs) are performed in order to assess whether a new drug shows some promise of activity for the disease [1]. Imagine that if all the patients with the disease were to be treated, the new drug would show some promise of activity to M of them, and therefore the response rate could be defined as p = M/N. Care must be taken to explicitly define what is meant by "show some activity" [1]. For example, the drug is said to show some activity to a cancer patient whose tumor shrinks by at least 50% after the treatment.
Glycogen storage disease type II (also known as Pompe disease) is an autosomal recessive metabolic disorder which damages muscle and nerve cells throughout the body. The disease affects approximately 1 in 140,000 babies and 1 in 60,000 adults a year [2]. Von Hippel-Lindau (VHL) disease is another rare autosomal dominant syndrome which affects 1 in 36,000 babies [3].
To conduct clinical trials for such extremely rare disease, the designs developed here are based on testing a null hypothesis that the true response rate is less than some uninteresting level ; that is, the new drug shows some activity to fewer than patients. If the null hypothesis is true, then we require that the probability of falsely concluding that the drug is efficacious is less than a user specified . We also require if a specified alternative hypothesis (that is, more than patients response to the drug) is true with , then the probability of falsely concluding that the drug is not efficacious is less than a user specified .
We start our discussion by considering the standard one-stage design for testing
vs. , or equivalently vs.
In order to test the above hypotheses, a sample of n patients selected randomly from the population of N patients is treated. Let S denote the number of patients in the sample who respond to the treatment, which is following the hypergeometric distribution, denoted as H (N; M; n),
Where ; ... ;. Consider the test with reject region , where is an integer such that . We can show that this test is Uniformly Most Powerful (UMP) test for hypotheses (1).
Group sequential designs are widely employed in phase II and phase III clinical trials. A group sequential test allows early termination of accrual if the treatment response rate of the treatment is quite high or quite low during early stages. Fleming [4], Chang, et al. [5], and Simon [6] pointed out that for binomial distributions; well-designed group sequential tests are more efficient than standard single-stage tests, because on average they require fewer patients to achieve the predesignated significance level and power. However, it is still unknown that for hypergeometric distributions, whether or not there exist exact group sequential tests which are more efficacious than the aforementioned standard single-stage exact test.
It is known that when the disease population size is large, the hypergeometric distribution can be approximately well by the binomial distribution where and then we can use the available designs [6]. But for extremely rare diseases, using designs based on binomial distribution may have incorrect significant level; that is, the true type-I error may be different from the pre specified type-I error. In Figure 1, we display a toy example, showing the difference between two distributions, hypergeometric distribution and binomial distribution , where
Motivated by Kepner and Chang [7,8], in this manuscript we show that, for hypergeometric distributions, under mild conditions and for a given number , there exists at least one k-stage group sequential test which has exactly the same maximum total sample size, significance level, and power as the standard single-stage hypergeometric test. Furthermore, motivated by Simon [6], we examine two types of optimal two-stage designs for a range of design parameters; one is optimal in the sense that the expected sample size under the null hypothesis is minimized, and the other is optimal in the sense that the maximum sample size is minimized.
The remainder of the manuscript is organized as follows. In Section 2, group sequential procedures are described. In Section 3, main theorems are presented and proved. In Section 4, two types of optimal two-stage designs are examined. Some brief discussion is given in Section 5 (Figure 1).
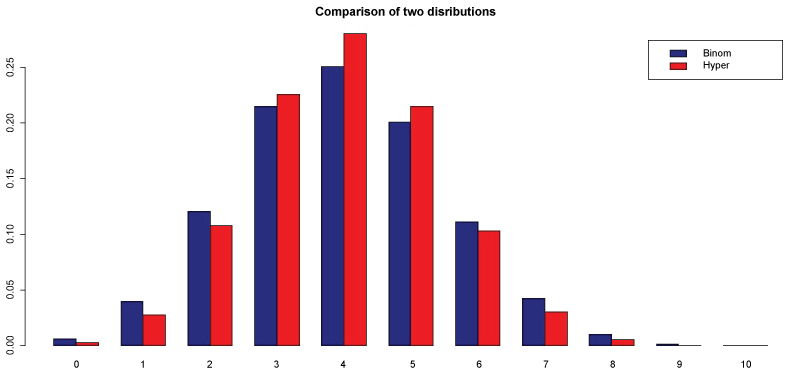 Figure 1: Comparing hypergeometric distribution
and binomial distribution , where . View Figure 1
Figure 1: Comparing hypergeometric distribution
and binomial distribution , where . View Figure 1
Group sequential tests are specified by the maximum number of stages, k, the cumulative number of patients to be treated up to each stage and the critical values, , where . Let be the number of patients who respond positively to the treatment among patients cumulative up to stage . The distribution of is where . The distribution is undetermined up to an unknown parameter, or equivalently, .
The group sequential tests are conducted as follows. Start with stage . If , stop sampling and reject ; if , stop sampling and accept ; if , continue to stage . At the final stage, accept if and reject if
The power function for any such group sequential test is
For the required significance level and power at , one should select and such that and . The power function can be written as a function of proportion . To abuse the notation slightly, let the power function (3) be written as . Therefore, for the required significance level and power at , where and , one should select and such that and .
As discussed in Kepner and Chang [7], there are three types of group sequential designs. Type 1 designs stop early only to conclude efficacy (i.e., stop early only to accept ), Type 2 design stops early only to conclude futility (i.e., stop early only to reject , and Type 3 designs stop early for either efficacy or futility. Using the above notation, Type 1 group sequential tests are those with , Type 2 group sequential tests are those with , and Type 3 group sequential tests are those with , for .
In this section, three theorems are established, one for each of three types of exact group sequential tests discussed in Section 2. These three theorems are similar to those established in Kepner and Chang [7] which were for binomial distributions.
Assume:
is the smallest sample size for which there is an integer b such that , , and , where ; is an integer such that .
Under the conditions (A1)-(A3), assume . Then there exists a Type 1 k-stage exact sequential test such that and the significance level of the test is and the power of the test at is at least .
Let and for . The test statistic at stage is . Let and . Since for , then the sample size and the critical values become a proper Type 1 k-stage test. According to this test, is accepted if and only if at least one , , which is equivalent to , since . Thus, the power function of the test is the same as that of S.
Under the conditions (A1)-(A3), assume . Then there exists a Type 2 k-stage exact sequential test such that and , the significance level of the test is and the power of the test at is at least .
Let and for . The test statistic at stage is . Let and for and . Since , and , then the sample size and the critical values become a proper Type 2 k-stage test. According this test is rejected if and only if at least one . That is, there exists at least one , , such that . This is equivalent to , because . Thus, the power function of the test is the same as that of S.
After Theorems 1-2 are established, following the same proof as that for Theorem 3 in Kepner and Chang [7], we can establish the following theorem.
Under the conditions (A1) - (A3), assume . Then there exists a Type 3 exact k-stage sequential test such that and , the significance level of the test is and the power of the test at is at least .
The implications of these theorems are two-fold. The theoretical implication is that, for a given number satisfying some mild conditions, there exists at least one k-stage group sequential test whose maximum total sample size is bounded above by the sample size needed for the standard one-stage test to achieve the same significance level and power. The applied implication is that we can search for "optimal" exact k stage designs among those proper group sequential tests whose maximum total sizes are bounded above by the sample size needed for the standard exact one-stage test to achieve the same significance level and power.
In this section we focus on optimal two-stage designs, which can be extended to optimal k-stage designs. We examine the two types of optimal two-stage designs proposed in Simon [6]; one is optimal in the sense that the expected sample size under the null hypothesis is minimized, and the other is optimal in the sense that the maximum sample size is minimized. Originally they were proposed for binomial distributions. In this manuscript, we examine them for hypergeometric distributions. But there is a small difference. In Simion [6], the optimal designs are searched among all the proper two-stage designs. Hereafter, thanks to Theorems 1-3, we only need to search for optimal designs among those proper two-stage designs whose maximum total sizes are bounded above by the sample size needed for the standard one-stage design to achieve the same significance level and power. Narrowing the search domain improves the computational efficiency.
Consider the first type of optimal two-stage designs. If there are patients in the first stage and, if necessary, more patients are treated in the second stage, leading to maximum sample size to be . Then the expected sample size is , where PET is the probability of early termination after the first stage. The decision of whether or not to terminate after the first stage depends on the type of the two-stage design (Type 1, Type 2, or Type 3) and the number of responses observed from those patients (Table 1). The expected sample size EN and the probability of early termination PET depend on the unknown parameter, M, the number of responses observed in the sample of size from the population of size N. In particular, . In this manuscript, as in Simon [6], we consider the optimal two-stage designs which have minimum expected sample size under the null hypothesis, where . The rationale behind this is that we should expose as few patients as possible to an ineffective treatment. The second type of optimal two-stage designs is easier to describe. They are the ones that have minimum maximum sample size; that is, is minimized.
Table 1: Notation for interpreting different designs. View Table 1
Now we are ready to examine these two types of optimal two-stage designs. First, we refresh notation for interpreting different designs in Table 1. We consider the following settings. Set significance level and Type II error rate . Set the population size N = 80 or 120, the proportion under the null hypothesis and the treatment effect or 0:2. The resulting optimal designs are presented in Table 2, Table 3, Table 4 and Table 5. We have obtained these results using R codes, which can be requested by sending email to the first author.
Table 2: N = 80. Designs for testing H0:p p0 vs. H1:p > p0 with = 0:05 and power at least 80% at p1 = p0 + 0:15. For each setting the Rows 1-3 contain the Types 1-3 two-stage designs. The left and rights parts are for the first type and second type of optimal designs. View Table 2
Table 3: N = 80. Designs for testing H0:p p0 vs. H1:p > p0 with = 0:05 and power at least 80% at p1 = p0 + 0:2. For each setting the Rows 1-3 contain the Types 1-3 two-stage designs. The left and rights parts are for the first type and second type of optimal designs. View Table 3
Table 4: N = 120. Designs for testing H0: p p0 vs. H1: p > p0 with = 0: 05 and power at least 80% at p1 = p0 + 0:15. For each setting the Rows 1-3 contain the Types 1-3 two-stage designs. The left and rights parts are for the first type and second type of optimal designs. View Table 4
Table 5: N = 120. Designs for testing H0:p p0 vs. H1:p > p0 with = 0:05 and power at least 80% at p1 = p0 + 0:2. For each setting the Rows 1-3 contain the Types 1-3 two-stage designs. The left and rights parts are for the first type and second type of optimal designs. View Table 5
Table 2 and Table 3 apply to a small population of size and Table 4 and Table 5 apply to a small population of size , where is 0:15 for Table 2 and Table 4 is 0:20 for Table 3 and Table 5. In each table, the first column corresponds to one-stage design, the optimal two-stage designs minimizing the expected sample size under are shown on the left half of the table, and the optimal two-stage designs minimizing the maximum sample size are shown in the right half of the table. For each setting, there are three rows, which are corresponding to three types of two-stage designs (Types 1-3), respectively. The tabulated results include the optimal design (Table 1), the expected sample size under , , the maximum sample size, , and the early termination probability under , . For some settings, there is more than one optimal design, of which the minimum maximum size is the same as the sample size in the one-stage design, then the one which has minimum expected sample size under is reported and it is indicated by an asterisk.
First and most importantly, the results in Table 2, Table 3, Table 4 and Table 5 verify the main theorems; that is, for each setting, there exists at least one two-stage design whose maximum sample size is bounded above by the sample size of the one-stage design. Because the early termination probability is strictly positive for any proper two-stage design, the corresponding expected size is always strictly smaller than the sample size of the one-stage design.
Second, in many settings, the maximum sample sizes of the two-stage designs are strictly smaller than the sample size of the corresponding one-stage design. This finding is striking, noting that the standard one-stage test is uniformly most power test.
Third, in some settings, the optimal two-stage design minimizing the expected sample size may be more attractive than the optimal two-stage design minimizing the maximum sample size. This is the case when the difference in maximum sample size is small, but the difference in expected sample sizes is large. For example, in Table 2, the third row in the session of indicates cases where the difference in maximum sample size is only one, but the difference in expected sample sizes is 7:5. For other settings, these two types of optimal exact two-stage designs are quite similar. Surprisingly, this finding is different from that in Simon [6], where it was concluded that the "minimax" designs may be more attractive.
Optimal exact group sequential tests for a binomial proportion have been well-studied in the literature, but a corresponding study involving hypergeometric distributions is lacking. This manuscript studies some exact group sequential tests involving hypergeometric distributions, which are useful for investigating treatment effects on rare diseases.
In this manuscript, three theorems have been proved and two types of optimal two-stage designs are presented. The theorems guarantee the existence of proper exact group sequential designs whose expected sample sizes are strictly smaller than the ones from standard one-stage designs. The discussed optimal two-stage designs provide two examples of how to design optimal two stage designs. There are other criteria; for example, the optimal design minimizing the expected sample size at a given parameter, say . Moreover, the tabulated results provide detailed comparisons between these two types of optimal designs.
Finally, this manuscript focuses on one-arm phase II clinical trials. One of our future projects is to study the properties of group sequential tests for comparing two hypergeometric distributions, which arise from two-arm phase II clinical trials.
The authors would like to thank two anonymous referees for their constructive comments and suggestions, which have led to a significantly improved paper.