The proposed concept is based on a physical approach towards the problem of aging and suggests a mathematical model of aging.
Developing a theoretical model of the aging reversing mechanism.
In the beginning of the century L. Boltzmann [1] was the first to represent the increasing entropy process as a time flowing characteristic. Besides, he pointed at a possible time reversion process in micro systems. A symbol of aging of any system - alive or inanimate is the entropy increasing. Is this process reversible? For short periods - yes and biological systems represent examples of it. Unfortunately, any reversing of the entropy sign in these systems is possible only for short periods of time and then the aging continues. There are many physical processes of this kind. This is a laser in a coherent mode, some oscillatory chemical reactions, where some reagent concentrations change coherently in the whole volume, coherent contraction of the heart. In astronomy - this is a galaxy forming from the dust clouds. All the mentioned processes are cyclic in time. The living systems are also cyclic. Different species have different life cycles stretching from 24 hours for some butterflies up to 10000 years for some cypresses. Among many figures of this kind, the human life longevity looks like the God's riddle to solve.
All living systems possess a DNA molecule, which controls the life longevity of a certain specie. Similar to the reversibility in physical systems, the living ones also manifest short periods of time evolution reversibility such as in rare cases of spontaneous self-cure from cancer and some other lethal diseases. That points at a principal possibility to reverse the aging process.
As it was shown [2] the Fermi-Pasta-Ulam auto recurrence proved to have a general biological meaning in the description of the electrical activity of such a sophisticated biological system as the heart. At the same time the mathematical interpretation of the DNA and RNA molecules as nonlinear distributed the Fermi-Pasta-Ulam auto recurrence resonators of the electro-acoustic waves [3,4] (a sort of a gigantic piano on which many melodies are constantly played with a recurrence to their initial notes) showed that the aging rate is probably controlled by the complex behavior of the electro-acoustic FPU wave recurrence spectrum in the DNA molecule similar to a great orchestra with musical instruments being slowly detuned. After a certain period, they need retuning. The role of rejuvenating "tuning forks" for human organisms can play the electro-acoustic FPU wave recurrence spectra excited in the sperm cells DNA or young donor blood cells DNA placed into the special resonators. Since the DNA molecule as well as the RNA molecule [4] have their own FPU recurrence spectra or group of "melodies", it can be "corrected" by special generators imitating the DNA molecular electro-acoustic vibrations. Because the DNA molecule grows older due to incorporation of different substances into its structure, applying of the "young DNA the FPU recurrence spectrum emission" on the organism, leads to its retuning and as a result to the rejuvenation. Another crucial problem of rejuvenation is exposing of the organism to the necessary geophysical environment characteristic for earlier years. It is a difficult but solvable problem. Since the geophysical background, the Earth magnetic field variations for example, have been registered for decades, it is possible to develop generators imitating the dynamics of the geophysical environment which was in previous years. Such a complex approach could control the aging process bringing in the rejuvenation of the organism.
Differ from the commonly accepted idea that the aging problem is a medico-biological one, the proposed concept is based on physics. Applying the "Young DNA FPU recurrence spectrum emission" on the organism, leads to retuning of the organismic DNA to its earlier state and as a result to the organism rejuvenation.
For the first time the DNA molecule was described as a Fermi-Paste-Ulam recurrence resonator in the framework of coupled the nonlinear Schrödinger and the sine Gordon equations in [3] and later the RNA molecule was described within the same format [4]. Using the Ginzburg-Landau chain [5], we can write a mathematical model of the dynamics of electro-acoustic oscillations in the DNA molecule having the FPU auto-recurrence with two degrees of freedom, in the form of the coupled Van der Pol equations with a time lag:
Where - the frequency of the dynamics of circular oscillations of the DNA molecule, k -the spatial frequency of longitudinal vibrations of the DNA molecule, - the value proportional to the longitudinal dynamic electrical potential of the DNA molecule, - the value proportional to the circular dynamic electrical potential of the DNA molecule, - the value proportional to the dispersion in the propagation of the electro-acoustic pulse along the DNA molecule, - the value proportional to the delay in the propagation of the electro-acoustic pulse around the DNA molecule, - the value proportional to the length of the DNA molecule, - the value proportional to the surface square of the DNA molecule, - the value proportional to the lowest frequency period of spatial electro-acoustic oscillations in the DNA molecule, - the value proportional to the lowest frequency period of circular electro-acoustic oscillations in the DNA molecule, - parametric coupling coefficients reflecting the degree of mutual energy interaction of the two types of FPU auto-recurrences in the DNA molecule, - the function of resonance effect on the DNA molecule thermal fluctuations of the intracellular fluid, - a function of the resonant rejuvenating effects on the DNA molecule electro-acoustic FPU recurrence spectrum of the DNA molecule obtained from the sperm, - ratios of the energies of the longitudinal and circular oscillations of the DNA molecules, - are constants.
Computer study of the system (1) shows that the model of electro-acoustic wave dynamics in the DNA molecule reproduces the picture of mutual energy interaction of the two types of the FPU auto-recurrences with a finite time longevity. Normal amplitudes of the electro-acoustic oscillations in the system (1) indicate a normal living period of the DNA molecule and the organism. Sharp decreasing of the amplitudes shows the decaying process of the DNA molecule bringing the end of the organism life. Figure 1 and Figure 2 show modeling of the life elongation process through increasing the DNA life duration by external influence of the DNA sperm molecule FPU recurrence electro -acoustic spectrum ( - the external function in the right part of the system (1)).
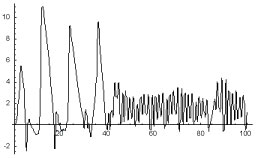 Figure 1: The amplitude of the DNA molecule electro-acoustic oscillations in the solution of the system (1) Simulating the normal DNA life longevity process, ending in decaying. Vert. Axis - potential, Horiz. Axis - time. Conditional units.
View Figure 1
Figure 1: The amplitude of the DNA molecule electro-acoustic oscillations in the solution of the system (1) Simulating the normal DNA life longevity process, ending in decaying. Vert. Axis - potential, Horiz. Axis - time. Conditional units.
View Figure 1
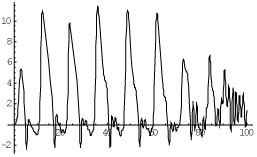 Figure 2: The life elongation process simulation through increasing the DNA life duration in the system (1) Solution to compare with Figure 1 as a result of the model external influence of the sperm DNA molecule emitting the FPU recurrence electro-acoustic spectrum enlarging the organism DNA molecule living period. ( - the external function in the right part of the system (1)). Vert. Axis - potential, Horiz. Axis -time. Conditional units.
View Figure 2
Figure 2: The life elongation process simulation through increasing the DNA life duration in the system (1) Solution to compare with Figure 1 as a result of the model external influence of the sperm DNA molecule emitting the FPU recurrence electro-acoustic spectrum enlarging the organism DNA molecule living period. ( - the external function in the right part of the system (1)). Vert. Axis - potential, Horiz. Axis -time. Conditional units.
View Figure 2
Computer simulation shows that the suggested approach corresponds to the mathematical problem of changing the Eigen functions of a non-linear distributed system - the DNA molecule by applying new boundary conditions of young cells DNA on this system changing the structure of the FPU recurrence spectrum in the aged DNA molecule. Therefore, the problem of aging and rejuvenation looks to be mathematical.