The drug development paradigm in oncology has changed in recent times as developments in science and technology have led to more targeted therapies. Drug products are receiving marketing approvals based on single randomized studies enrolling 100-200 patients, including early phase (phase II) clinical trials. In this paper, we examine the likelihood of observing a significant treatment effect when in fact the true treatment effect is modest to null by exploring a range of sample sizes via simulation studies. Results showed that the Cox model performed appropriately in studies as small as n = 50 and extreme treatment effect estimates were very rarely observed when the true treatment effect was modest to null, at least for the examples considered under our assumed conditions. It appears that a hazard ratio of large magnitude observed in a small study is likely to be indicative of a true treatment effect, although of uncertain magnitude. However, the simulation assumes a well-conducted study with minimal to no amendments or adaptations and a non-ambiguous endpoint, which unfortunately is not often the case in the early phases of drug development. As the paradigm in oncology changes, randomized phase II studies can no longer be seen as simply supporting go/no-go decisions. When promising drugs are evaluated in trials with overall survival as an endpoint, companies may want to consider providing a pre-specified contingency statistical analysis plan in anticipation of unexpectedly promising survival results.
A total of 345 skin surface swab samples were collected from clinically diagnosed common wart (n = 166), plantar wart (n = 142), flat wart (n = 5), both common and plantar warts (n = 15) and common and flat warts (n = 1). DNA extraction and amplification were carried out using an established PCR, FAP primer pair-based method to detect HPV DNA. We measured HPV DNA negative samples by PCR with β-globin primer pair to confirm the availability of DNA.
Clinical trials, Small sample, Log-rank test, Cox model, Hazard ratio
Oncology drug development has seen a paradigm shift in recent years as innovations in science and technology have led to the development of new and effective targeted therapies. The perceived effectiveness of these new therapies has led to questions regarding the ethical appropriateness of traditional drug development when early phase studies show large treatment effects with limited toxicity [1-4]. The increased desire for earlier access to new therapies, along with the subsequent passage of the FDA Safety and Innovation Act of 2012, has allowed for the FDA's conscious efforts to implement expedited programs such as Fast Track, Breakthrough Therapy, Accelerated Approval, and Priority Review for serious conditions [3-5]. As a direct result of this, there have been an increasing number of oncology drug approvals based on single randomized studies enrolling small populations of 100-200 patients, often in early phase clinical trials. Early phase studies by nature are often plagued by conduct issues, so expediting effective therapies to market while maintaining statistical rigor and regulatory scrutiny is an important issue the FDA is facing that must be explored further [6].
Early phase trials are not designed for registration purposes, so their design and conduct open up great potential for uncertainty. First of all, these trials are often conducted in small populations. Redman and Crowley warned that small randomized studies often result in unstable estimates of efficacy and may not be large enough to balance potential prognostic and predictive factors between arms [7]. Tuma emphasized the issue of heterogeneity in phase II populations [8].
Secondly, there are concerns related to study conduct in early phase development as it is generally set with more liberal operating characteristics. Lara and Redman cited concerns by Redman and Crowley and Tuma [7-9] regarding the limitations of randomized phase II designs and further pointed out that positive phase II studies do not necessarily result in positive phase III studies noting "the predictive value of a phase II study is a function of the quality and design of the study and not whether it involved a randomized comparison or not." It should be noted that a dampened effect in phase III following a promising phase II result is neither uncommon nor unexpected. The FDA (2017) published a report [10] of 22 case studies where phase III results were divergent from their phase II counterparts in safety, efficacy, or both. The breast cancer drug iniparib was one of the cases described in the report and represents an extreme case in which a promising phase II trial led to a failed phase III trial. Proposed explanations for iniparib's failure in phase III included poor study design in phase II in which crossover may have given it an inadvertent advantage, the possibility of a false positive statistical result and the heterogeneity of triple-negative breast cancer, and the fact that iniparib likely did not work as promoted [11]. These are all examples of conduct and trial design issues common to early phase studies. Other examples of such issues include unplanned interim looks as well as data-driven changes and modifications.
Lastly, the endpoints assessed in early phase are often more ambiguous. For example, progression-free survival is susceptible to ambiguity with respect to the frequency of assessment and progression determination.
Assuming a well-conducted study with an unambiguous endpoint such as overall survival, the major cause for concern that remains with approving indications based on randomized phase II studies is their small sample size. In fact, the FDA report [10] on divergent results between phase II and phase III was intended to show how "controlled trials of appropriate size and duration contribute to the scientific understanding of medical products." In general, small sample sizes are not problematic since studies designed to detect a large treatment effect are expected to be small. The performance of Cox models, which are typically used to estimate the hazard ratio, also should not be problematic in small sample settings. Johnson, et al. [12] has assessed the small sample performance of Cox models in estimating regression parameters in a two-covariate hazard function model, and they cited an earlier report that considered the simpler single variable case. The general conclusion was that in ideal conditions of balanced covariates and no censoring, results were reasonable for samples of size 40 or greater in terms of bias, asymptotic versus finite-sample variance, and power [12]. But, bias increases when the treatment and control groups are unbalanced [12].
However, the situation emerging in oncology drug development is that more and more phase II trials designed for go/no-go decisions are observing treatment effects much larger than what they were initially designed to detect. In these cases, the trials have small sample sizes because they were not meant for registration and were thus designed to allow for high type-1 error. Since the trials were designed to detect a smaller treatment effect than what was observed, and heeding Redman and Crowley's [7] warning, there is concern that the promising result could have occurred by chance alone.
Simulation studies were conducted, under the assumption of a well-conducted study with an overall survival endpoint, to explore the likelihood for results to be inflated in a small sample study and to what extent they can be believed. Results from these simulations will help provide general insight as to how these situations maybe addressed in the future.
Consider an example study scenario where the accrual period was 12 months with an 18 month follow-up period. Patient start times were generated from a uniform (0,12) distribution, and the failure time for each patient was generated from a distribution with hazard function.
Where Z = 1 for the experimental treatment arm and Z = 0 for the control arm, with a constant baseline hazard function over time, for all time t.
A series of trials were simulated with various true hazard ratios representing effect sizes from moderate to null (i.e. HR = 0.7, 0.8, 0.9, and 1), sample sizes, and control medians for overall survival, as summarized in Table 1. These settings were chosen to explore the effect of sample size on hazard ratio estimates, when the true hazard ratio shows moderate to no treatment effect, and whether that effect is further affected by the length of median survival (i.e. the percentage of censored observations).
Table 1: Simulation scenarios for each assumed true hazard ratio. View Table 1
Hazard ratios were estimated using the Cox model which is usually specified in oncology trial protocols. Treatment magnitude was quantified under the following assumptions: HR = 1 represents no effect, HR = 0.9, 0.8, and 0.7 represent moderate effects with HR = 0.7 serving as the threshold between moderately effective and ‘clinically’ effective and any HR < 0.5 is considered an extreme effect.
Each data configuration shown in Table 1 was replicated 5,000 times, and the following values were recorded (1) The average percentage censored; (2) The empirical bias of β, calculated as the mean of the β estimates from the Cox model minus the true value; (3) The empirical standard deviation (ESD) of β, calculated as the standard deviation of the β estimates from the Cox model; (4) The average asymptotic standard error (ASE) of β, calculated as the mean of the standard errors of β given by the Cox model; (5) Hazard ratio estimates from the Cox model; and (6) The proportion of HR estimates from the Cox model that were less than 0.3, 0.4, and 0.5.
Simulation results are summarized in Table 2, Table 3, Table 4 and Table 5 by true hazard ratio, and Figure 1 shows density plots for the hazard ratio estimates by true hazard ratio and control median for select sample sizes. The simulation results in Table 2 assume no treatment effect (HR = 1). When the sample size was large (n ≥ 200), the results showed no instances in which an extreme treatment effect (HR < 0.5, 0.4, or 0.3) was detected. Even at smaller sample sizes (n < 200), extreme treatment effects occurred very rarely. The proportion of hazard ratios less than 0.5 under the most extreme scenario, where control median was 24 months and sample size was 50, was less than 6%. Simulation results in Table 3, Table 4 and Table 5 assume modest treatment effects of HR = 0.9, 0.8, and 0.7, respectively. Here incidences of extreme treatment effects (HR < 0.5, 0.4, or 0.3) increased as sample size decreased, but overall there was still a fairly low number of such occurrences with the maximum proportion being < 25% in the most extreme scenario (true HR = 0.7, control median = 4 months and n = 50). Overall, the highest number of extreme effects occurred when the true hazard ratio was 0.7 in which case a hazard ratio of 0.5 would likely not be considered extreme. Even then, the proportion of hazard ratios less than 0.3 remained small (< 5%).
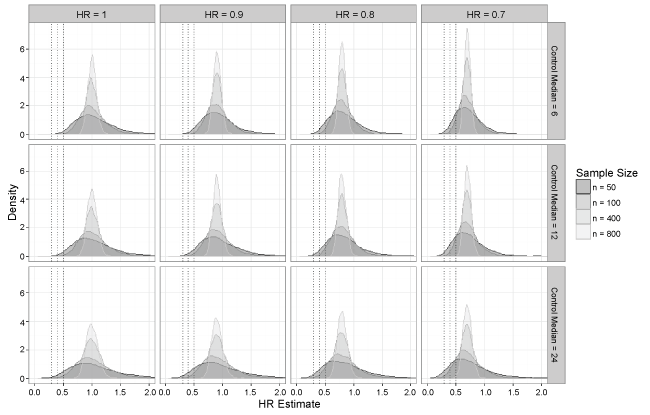 Figure 1: Density plots of hazard ratio estimates as sample size changes across all control median and true hazard ratio specifications.
View Figure 1
Figure 1: Density plots of hazard ratio estimates as sample size changes across all control median and true hazard ratio specifications.
View Figure 1
Table 2: Simulation results when true hazard ratio = 1. View Table 2
Examining the operating characteristics of the Cox model in Table 2, Table 3, Table 4, and Table 5, it appears the conclusions of Johnson, et al. [12] were upheld under the settings for this simulation. While a formal test for non-proportionality was not conducted, it is assumed that the proportional hazards assumption holds, as the simulated data were generated from identical exponential distributions. Biases remained close to zero with no noticeable pattern as sample size decreased, even as control median and true hazard ratio vary. The ASE and ESD were very similar across all settings, and note that ASE and ESD both appeared to increase as the sample size decreased or the control median increased. The median hazard ratio estimate was consistent with the true hazard ratio across all simulation scenarios.
Table 3: Simulation results when true hazard ratio = 0.9. View Table 3
Table 4: Simulation results when true hazard ratio = 0.8. View Table 4
The density plots in Figure 1 show that the spread of estimates increased as sample sizes decreased, so it does appear that small studies are prone to overestimate the effect size, which has been noted in the literature [13]. It should be noted that the effect size can be underestimated as well, but this is likely not a concern in terms of regulatory decision-making. Recall that incidence of extreme treatment effects was generally low, as seen in Table 2, Table 3, Table 4, and Table 5, with the highest number of observed extreme effects understandably occurring when the true hazard ratio was 0.7. These two observations taken together show that while an observed extreme treatment effect is most likely inflated, there is evidence the underlying true hazard ratio is likely to be 0.7 or better, which would represent a slightly diluted but still meaningful effect.
Table 5: Simulation results when true hazard ratio = 0.7. View Table 5
The impact of an unequal allocation ratio of 2:1 (treatment to control), a commonly used unequal allocation ratio in oncology clinical trials, was explored on select data configurations. Table 6 shows some of these results, which were fairly consistent with what was seen with equal 1:1 allocation. Biases remained small, ASE and ESD values were similar, and the median hazard ratio estimates were consistent with the true hazard ratios. The increased bias with unequal allocation ratio (1:4) as pointed out in Johnson, et al. [11] was not observed under the settings considered (2:1) for this simulation.
Table 6: Select simulation results with unequal allocation. View Table 6
Olaratumab was approved in October 2016 on the basis of an early phase randomized trial and can be used to illustrate the various challenges, regulatory and otherwise, involved with observing unexpected results in randomized phase II trials originally designed for go/no-go decision-making [14]. The olaratumab trial was a phase 1b/2 trial in 133 patients with advanced soft-tissue sarcoma with investigator-assessed progression-free survival (PFS) as the primary endpoint and overall survival (OS) as one of the secondary endpoints. The trial was designed to detect a difference for PFS at a two-sided significance level of 0.2 with a power of 0.8, and multiplicity adjustment was not planned for all secondary endpoints including OS. Results of the trial showed a moderate 2.5 month improvement in estimated median PFS with a stratified HR of 0.67 that was statistically significant at the two-sided 0.2 level. However, an unexpectedly large improvement of 11.8 months in estimated median OS with an unstratified HR of 0.52 was observed. While the PFS improvement on its own would likely be unremarkable in such a trial, olaratumab was granted accelerated approval largely on the basis of the OS benefit seen, despite the limitations in the trial design with respect to sample size and the set operating characteristics.
To further assess the unexpected survival benefit seen in this trial, we performed the following simulation. Data settings were chosen to mimic the olaratumab trial. The sample size was set at n = 130 patients, the accrual period was 12 months with approximately 40 months of follow up, and median survival was set as 14.7 months on the control arm. Under these specifications, data were generated to explore scenarios where the true treatment effect was modest to null as quantified by a series of hazard ratios from 0.7 to 1. Each scenario was replicated 5,000 times and the same values as in the previous simulation were recorded.
Results are shown in Table 7. The average number of events on the control arm in each case (57 events) is comparable to the actual number of events observed in the control arm of the olaratumab study (52 events), indicating that the simulation settings adequately mimicked those of the original study. As with the previous simulation, operating characteristics of the Cox model showed its small sample performance to be sound. Biases are small, ASE and ESD values are similar, and the median hazard ratio estimates align with their true values.
Table 7: Olaratumab simulation results. View Table 7
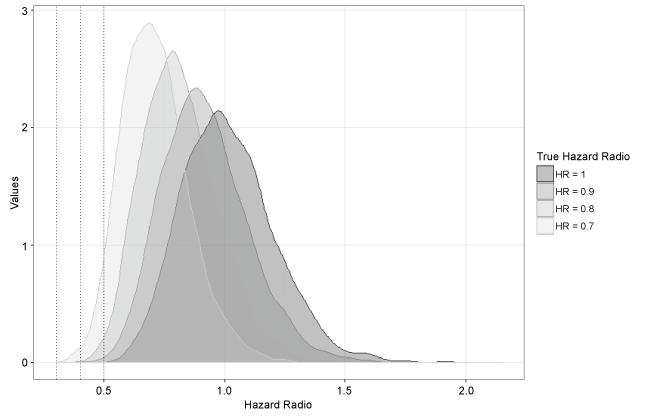 Figure 2: Density plots of hazard ratio estimates under each true hazard ratio.
View Figure 2
Figure 2: Density plots of hazard ratio estimates under each true hazard ratio.
View Figure 2
Figure 2 shows density plots of the hazard ratio estimates under the different true hazard ratios considered. The spread of the estimates is similar across settings as the sample size in the simulation remained constant at n = 130. Although the spread is quite wide due to the small sample size, it still barely covers any extreme hazard ratios of magnitude less than 0.5 until the truth is around HR = 0.7. Thus these results are supportive of the claim that it is unlikely the extreme result seen in the olaratumab trial was completely due to chance.
Under the new oncology drug development paradigm, it is clear that randomized phase II trials can no longer be seen as simply supporting go/no-go decisions. It is becoming more and more common for products to receive accelerated approval based on the results of small randomized studies not initially designed for registration when a large magnitude of benefit is observed. Thus, it is important to be confident that these promising results are due to truly effective innovative therapies without hesitation that they could be chance findings. The simulation studies described above were conducted to address concerns with small sample studies by assessing the likelihood of observing a large treatment effect when the true effect was actually modest to null.
Results from the simulation studies conducted have helped improve confidence that the effects observed are not likely due to chance, although they are most likely of smaller magnitude. They have also helped reinforce that observing a moderate effect in a small study is questionable, as the true treatment effect could be even more modest to null. In both cases, there is still potential for the confidence intervals associated with these hazard ratio estimates to be wide. However, limitations to the simulation included assuming proportional hazards and ignoring the effect of switchover of patients in the control arm to receive experimental treatment after disease progression. Thus, these results are limited solely to the simulation settings considered here.
Concerns also still remain for early phase studies as the simulation does not address issues brought up by Lara and Redman [9], regarding study quality and design in phase II, as well as Redman and Crowley [7] and Tuma [8], regarding imbalance in prognostic and predictive factors in small studies and heterogeneity in phase II populations. It was previously noted that it is not uncommon for larger confirmatory studies to find smaller magnitudes of benefit compared with smaller early phase studies. It has become clear that the reason for this difference goes beyond the small sample size issue. In fact, the reason may have more to do with poor study conduct in the form of unplanned interim looks, data-driven changes, ambiguous endpoints, as well as population heterogeneity. The FDA review for olaratumab [14] noted that there are still concerns about the heterogeneous population of the small study and a further randomized trial will be needed to generalize to other patient subgroups.
At the 2016 Friends of Cancer Research Annual Meeting [6], a panel consisting of regulatory, industry, and academic representatives discussed the optimization of exploratory randomized trials. It was noted that, moving forward, efforts need to be made to prospectively design trials that can potentially support both go/no-go decisions as well as registration. As one potential option, one panelist [6] presented a Bayesian analysis of unexpected survival “significance” in a randomized phase II trial. He proposed a method that combines prior beliefs about a hazard ratio with the results seen in the clinical trial to compute a posterior probability distribution of the hazard ratio. For example, this can then be used to get the posterior probability that the hazard ratio is ≤ 0.75 or 0.70, thresholds defined as being at least minimally clinically significant.
The olaratumab approval was an example case in which a randomized phase II trial for a promising drug with breakthrough therapy designation planned on evaluating overall survival. For cases that meet similar criteria, it may be worthwhile for pharmaceutical companies to have a pre-specified contingency statistical analysis plan in anticipation of unexpectedly promising survival results. There are no set guidelines for how such a plan should be implemented. However, it should be understood that a well-conducted study of this sort would include a planned hypothesis for each of the endpoints considered and planned analysis timelines, absent from any ad-hoc or exploratory analyses until the final analyses are completed. In addition, clear pre-specified rules for increasing sample size should be included. For example, if the observed hazard ratio is < 0.5, then no sample size adjustment is needed. If the observed hazard ratio is between 0.5 and 0.75, a sample size increase might be needed. If the observed hazard ratio is greater than 0.75 then perhaps a phase 3 trial should be considered. The thresholds used here are for illustration purposes only. They are subject to change and should be dependent on disease setting, the comparative control treatment, and available therapies.
It goes without saying that Phase III trials still remain the standard for determining clinical benefit for the majority of products. Even when phase II trials are designed with our proposed considerations in place, approval should remain in the setting in which the trial was conducted and results should not be extrapolated to earlier settings or particular subgroups. Any such claims need to be studied on their own in a separate phase II or phase III study as appropriate. As the oncology drug development paradigm continues to shift, it will be increasingly important for FDA and industry to work together to find innovative design solutions in order to confidently have effective drugs available for patients in need in a timely manner.