International Journal of Clinical Biostatistics and Biometrics
A Constrained Non-inferiority Approach for Assessing Clinical Efficacy to Establish Biosimilarity
Jason JZ Liao*
Novartis Pharmaceuticals, One Health Plaza, East Hanover, NJ 07936, USA
*Corresponding author:
Jason JZ Liao, Novartis Pharmaceuticals, One Health Plaza, East Hanover, NJ 07936, USA, E-mail: jason.liao@novartis.com
Int J Clin Biostat Biom, IJCBB-1-008, (Volume 1, Issue 1), Research Article; ISSN: 2469-5831
Received: November 08, 2015 | Accepted: December 01, 2015 | Published: December 03, 2015
Citation: Liao JJZ (2015) A Constrained Non-inferiority Approach for Assessing Clinical Efficacy to Establish Biosimilarity. Int J Clin Biostat Biom 1:008. 10.23937/2469-5831/1510008
Copyright: © 2015 Liao JJZ. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
To develop a biosimilar product, it is necessary to demonstrate biosimilarity between the proposed biosimilar product and the reference product in terms of the purity, potency, efficacy, and safety. In this paper, clinical efficacy data required for establishing biosimilarity are considered. Non-inferiority (NI) and equivalence methods are commonly used for analyzing clinical trials to meet this requirement. The equivalence approach often requires large, costly, and lengthy clinical trials. The non-inferiority approach while requiring somewhat smaller trials are not accepted by all as adequately addressing the similarity issue between the proposed biosimilar product and the reference product as they do not rule out the prospect that the biosimilar product has increased activity which might be associated with more adverse effects. To address some of the challenges faced by the use of non-inferiority or equivalence methods, a constrained non-inferiority (cNI) approach is proposed to address both the clinical efficacy of the biosimilar product and the similarity to the reference product. The performance of the proposed constrained non-inferiority approach for analyzing a biosimilar trial is demonstrated through simulation and examples.
Keywords
Biosimilarity, Constrained non-inferiority (cNI), Effect preservation, Efficacy, Equivalence, Non-inferiority (NI), Plausibility interval, Power, Type I error
Introduction
In order to reduce health care costs and to increase accessibility, the development of biosimilars or Follow-on Biologics has received a lot of attention lately in the US. Biologics were 7 of the top 10 bestselling drugs in 2012, 2013 and 2014 including 6 mAbs [1-3], and the Congressional Budget Office had projected savings from $42 billion on the low end to as high as $108 billion over the first 10 years of biosimilar market formation to the US economy [4]. With the Biologics Price Competition and Innovation Act of 2009 and subsequent passage into law in 2010, a legal pathway exists in the US for the approval of biosimilars. Although many details surrounding statistical approaches still need to be sorted and clarified, in February 2012, the FDA released two draft guidances related to biosimilars and an accompanying Q & A document to aid Sponsors in the development of biosimilars [5-7]. In the EU, the product specific legal pathway was formed in 2001 and then later revised. Regulatory guidelines began appearing in 2005 and there have since been many additional guidelines published [8,9]. However, similar to the FDA guidances, the guidelines did not provide any details around statistical methods to be used in the establishment of biosimilarity [10].
A biosimilar product is a biological product that is highly similar to the reference product notwithstanding minor differences in clinically inactive components. There can be no clinically meaningful differences between the biosimilar biological product and the reference product in terms of the efficacy, safety, purity, and potency of the product. Due to the biological complexity and unlikeliness of being structurally identical to the reference product, many potential differences between the proposed biosimilar product and the reference product can arise, which can potentially significantly affect the efficacy, safety, purity, and/or potency. Thus, a direct head to head comparison is needed between the proposed biosimilar product and the reference product with respect to the structure, function, animal toxicity, human pharmacokinetics (PK) and pharmacodynamics (PD) if applicable, clinical immunogenicity, and clinical safety and effectiveness.
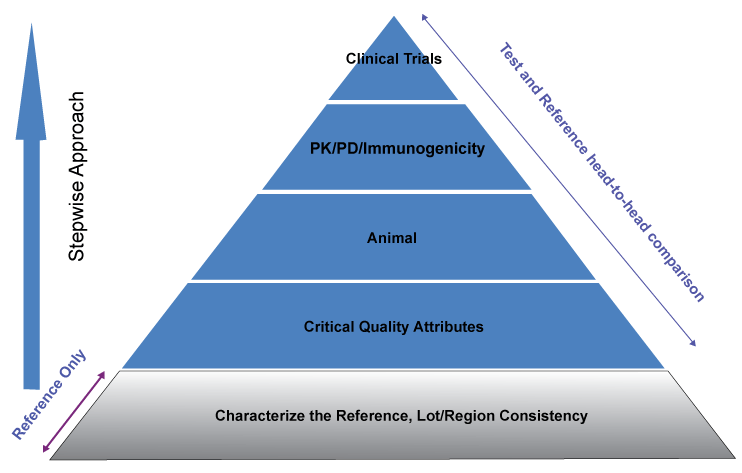
As specified in the FDA guidances [5-7], a totality of the evidence in a stepwise approach fashion is recommended for demonstration of biosimilarity between the test and the reference products. As outlined in the guidances, the information submitted in the application for biosimilars should include the structural and functional characterization, nonclinical evaluation, human PK and PD data, clinical immunogenicity data, and clinical safety and efficacy data, and this stepwise approach can be illustrated graphically as shown in figure 1, where extensive characterization of the reference using fingerprint-like techniques and the variability assessment of the reference using different lots, regions, and time shifted reference products are performed to define the reference target product profile before the direct head-to-head test-reference comparison. Note that the figure 1 here is similar to the figure described by Babbit and Nick [2011] but the reference characterization part is added [11].
A rich literature exists for comparing the efficacy of two products using non-inferiority or equivalence approaches [12-15]. Much recent discussion has centered on the use of synthesis or fixed-margin approaches where historical trials with the reference product are used in concert with a new trial comparing test to reference in order to demonstrate non-inferiority or equivalence. The fixed-margin approach determines the margin ahead of the new trial and traditionally uses the lower limit of a 95% confidence interval based on a meta-analysis of historical trials comparing reference to placebo. The synthesis method combines the results from the historical trials with the current trial to determine non-inferiority or equivalence. Of note, Snapinn and Jiang [2008a] demonstrated that an appropriately chosen synthesis method controls type I error while always providing higher power than the traditional fixed-margin approach described above [12]. FDA guidance also discusses these approaches [16].
In the setting of biosimilars, the equivalence approach to establish similar efficacy can lead to large clinical trials that are expensive and take a long time to conduct. The cost, risk, and length of time required to establish biosimilarity in clinical trials using traditional equivalence approach adversely affects the economic viability of their development. Though non-inferiority (NI) requires a smaller trial compared to the equivalence approach, the non-inferiority approach does not rule out the prospect that the biosimilar product is more efficacious, leading to concerns by some that test is not similar enough to reference with potential increased activity which might be associated with more adverse effects. Therefore, the use of non-inferiority rather than equivalence trials remains controversial. In order to realize a greater cost savings to the public by having more biosimilars on the market sooner rather than later, there is interest in considering alternative approaches that require less sample size but address the necessary requirement for demonstrating the biosimilarity. One such approach is proposed here. In section 2, the proposed constrained non-inferiority (cNI) approach is described. A simulation study is conducted to compare the power and the type I error of the proposed constrained non-inferiority approach to traditional non-inferiority and the equivalence approaches in section 3. Examples are used to illustrate the proposed approach in section 4, and a summary follows in section 5.
Methods
To demonstrate the similarity of clinical efficacy in support of biosimilarity of the proposed biosimilar product (T) to the approved reference product (R), as with other approaches, the available data from the historical trials comparing R with placebo (P) and from a new biosimilar clinical trial directly comparing T with R will be used. Without loss of generality, we assume the efficacy is measured on some arbitrary scale such that a larger value represents better efficacy. Further, we assume that the summary statistic measuring efficacy can be reasonably assumed to have a normal distribution, where treatment effect can be measured in, for example, the mean difference between groups, the log-odds ratio, the log-relative risk, or the log-hazard ratio.
Let γRP be the true effect of R relative to P and γTR be the true effect of T relative to R. Therefore, γTR + γRP represents the true effect of T relative P. Let BRP and VRP be the estimate of γRP and the estimated variance of that estimate, respectively, based on a meta-analysis of the appropriate historical clinical trials. Similarly, let BTR and VTR be the estimate of γTR and the estimated variance of that estimate based on the new biosimilar clinical trial.
Three approaches to assess the biosimilarity between T and R will be compared with a fixed margin and synthesis approach for each.
1. Non-inferiority (NI) approach
In this approach, given a margin δ, the goal is to demonstrate the proposed biosimilar product T is not worse than the reference product R by more than δ. The choice of the non-inferiority margin raises a lot of discussion in the literature. However, no matter what the margin is, in order for this approach to be valid, the margin δ must not be larger than the true effect of R (i.e., the δ must be less than or equal to γRP). One common approach for selecting δ is to pick a value that preserves at least some non-zero fraction, f, of the effect of R. This could be based on the lower limit of the 95 percent confidence interval for the reference product relative to the placebo, i.e., , a common fixed margin approach and part of the 95-95 approach where the 95% confidence interval (CI) for γTR is compared to this margin. Thus, the hypotheses for non-inferiority are
If a fixed-margin is used, the non-inferiority is established if , i.e.,
If a synthesis margin is used, then the non-inferiority is established [12] if
Note that FDA guidance prefers the fixed margin for the NI approach [16]. However, it is of interest to note that the left side of these equations will always be larger for the synthesis approach (the terms in the denominator are > 0 and ), and hence the synthesis method is uniformly more powerful than the 95-95 fixed margin approach, or more generally, than any double CI based fixed margin approach provided that the assay sensitivity and constancy are accounted for in order to control the type I error. Thus, both the fixed margin and the synthesis margin approaches are used to demonstrate the performance of all methods in the simulation.
A commonly used value that is referenced as a reasonable starting point for discussion in FDA guidance is f = 0.5, i.e., 50% effect preservation [16]. This value will be utilized for illustrative and comparative purposes in the simulation study and the illustration examples presented later in this paper.
2. Equivalence approach
The hypotheses for equivalence are
or VS
If the fixed margin is used, then equivalence is established if and , i.e.,
Using a similar argument as in the non-inferiority case, if a synthesis margin is used, then equivalence is established if
3. Constrained non-inferiority (cNI) approach
It is a well-known fact that an equivalence approach requires much larger sample size to achieve the same power as the non-inferiority approach, but that the non-inferiority approach only guarantees that the test product is not inferior to the reference product. These two have different merits and concerns. Is it possible to have an approach using a similar sample size of NI approach but also address the similarity? As mentioned in the FDA guidance, it is necessary to show that the proposed biosimilar product has neither decreased nor increased activity compared to the reference product [5-7]. Decreased activity ordinarily would preclude licensure of a proposed biosimilar product. Increased activity might be associated with more adverse effects, or might suggest that the proposed biosimilar product should be treated as an entirely different product with superior efficacy. Thus, the traditional NI plus additional constraints to ensure the two products are similar should address this issue. The cNI approach represents a middle ground where greater evidence is required to demonstrate that test is no worse than reference, but that some evidence/constraints supporting that test is not more efficacious than reference is also required.
Recall that the summary statistic measuring efficacy was assumed to have a normal distribution, which is determined by two parameters: the mean and the variance or range. The similarity constraints can be based on these two parameters. If there is a scientific/clinical justifiable threshold value for how similar the two products should be, then this threshold value should always be used to judge the biosimilarity between the proposed biosimilar product and the reference product. However, this is usually not a feasible task. The assessment of how similar the proposed biosimilar product and the reference product are to each other is not necessarily straightforward since how similar is similar enough is not well defined and scientific/clinical judgment may not be easy [17]. When coming to the clinical stage developing biosimilar efficacy, the biosimilarity has been demonstrated in terms of the critical quality attributes, in animals, and PK/PD/immunogenicity, and the left behind is the residual uncertainty of the biosimilarity. Consider a hypothesized trial where the test (the proposed biosimilar product) is also the reference. After the trail, there is usually an observed difference in the measuring efficacy statistic so that the difference is not zero, such as the relative risk is not 1, odds ratio is not 1 and the hazard ratio is not 1. Even though the observed difference is not zero, the reference product is an approved product, and therefore the test (here it is the reference also in this hypothesized trial) should almost always be comparable to the reference (itself). If this hypothesized trial is repeated many times, then a range will be obtained for the statistic measuring efficacy. Thus, the observed range can serve as a constraint and goalpost for judging similarity.
Based on all the above considerations and in order to address some of the challenges faced by the use of non-inferiority or equivalence methods, a cNI approach is proposed to address both the clinical efficacy of the biosimilar product and the similarity to the reference product. The cNI approach includes two objectives: 1) T is not inferior to the reference product R; and 2) T and R are comparable in distribution for the clinical endpoint. If these two objectives are achieved, then T and R are claimed to be biosimilar.
Note that the proposed cNI approach has an extra constraint for the statistical similarity in addition to the efficacy condition using the statistically powered non-inferiority approach. The condition 1 guarantees that the proposed biosimilar T does not have a decreased activity and the condition 2 guarantees that the proposed biosimilar T does not have an increased activity. With the assumption of a normal distribution for the summary statistic measuring efficacy, only the mean and the variability or range need to be compared and constrained. To show that T and R are comparable in distribution for the clinical endpoint, it must be demonstrated that a) the 95% CI for the treatment effect of T/R is within a plausibility interval (PI) of the treatment effect of R/R; and b) the point estimate for the treatment effect of T/R is within a boundary, say, for example, (0.8, 1.25). The plausibility interval of the treatment effect of R/R can be constructed using the idea that any observed difference between the reference against the reference itself should be considered nonclinical meaningful, and is defined as , where σ2R is the total variability for the reference [Liao, 2013] [18]. An appropriate k-factor along with the mean constrain boundary should be chosen to control the type I error level and the total reference variability should be adjusted for known factors and biases to avoid an inflated variability estimate. The second condition for the point estimate of the treatment effect of T/R within a boundary is to ensure that the T and R do not have too much effect difference due to the large reference variability from a less-controlled trial. Different constraints for the mean and range can lead to different cNIs. This condition will require adequate sample size and a well-controlled biosimilar trial. This should not be a concern since the proposed biosimilar clinical trial should at least satisfy the non-inferiority criteria with certain statistical power.
In summary, the proposed cNI approach for claiming biosimilarity depends on two facts. The first is passing the classical NI requirement to ensure the proposed biosimilar product not inferior to the reference product. The second is meeting the constraints that the point estimate of T/R is within the pre-defined mean boundary and the 95% CI of T/R is within the predefined plausibility interval to ensure the proposed biosimilar product not having an increased activity.
Evaluation of Methods
To compare the performance of the three methods mentioned in previous section in terms of type I error and power, a simulation study was conducted for the following three scenarios where the smaller rate is considered as better:
Case 1: P = 0.5, R = 0.3, T = 0.4
Case 2: P = 0.5, R = T = 0.3
Case 3: P = 0.5, R = 0.3, T = 0.2
Case 1 represents that both T & R are better than P but T is worse than R. Case 2 represents that T & R are the same and both are better than P. Case 3 represents that both T & R are better than P but R is worse than T. For the simulation study, the same placebo-controlled historical trial (or meta-analysis result) was used for all three cases with each arm having 300 subjects. Different sample sizes were evaluated for the current biosimilar trial comparing T to R. Cases 1 and 3 are used to evaluate the type I error of the three methods while case 2 is used to evaluate the power of the three methods. For each simulation sample point, both a historical placebo-controlled trial and a current biosimilar trial are simulated, and then a decision on similarity is derived using the simulated data. For each set of parameters, 5000 simulation samples were generated. For comparison, the same f = 0.5, i.e., 50% effect preservation was used for all three approaches. The probability of accepting the "biosimilarity" conclusion is plotted against the sample size per arm used in the current biosimilar trial for each case for using both the fixed and the synthesis approaches.
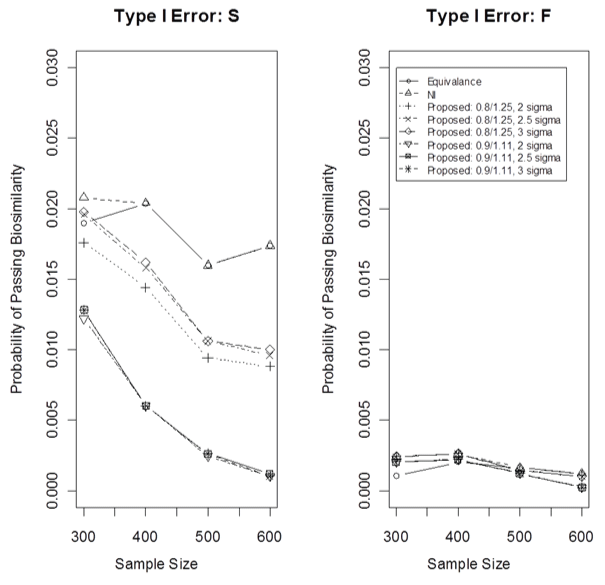
Figure 2 displays the type I error in case 1 for three methods using both the fixed and the synthesis approaches, where the proposed cNI approach used 3 different k values in the PI and two different boundaries for the mean which leads to six different cNIs. As the sample size in the current biosimilar trial increases, the type I error decreases. All cases have the type I error controlled very well. Note that the NI approach is one-sided but the cNI and the equivalence approaches are two-sided. The proposed cNI approach has more options to control the type I error. Figure 2 indicates that both the k- value and the mean boundary have an impact on controlling the type I error. The smaller the k- value, the better controlling the type I error. The tighter the mean boundary, the better the control of type I error. It seems that the mean treatment constraint boundaries in the proposed cNI approach controls the type I error more effectively than the k-value. In general, the synthesis approach gives a little larger type I error than the fixed margin approach for all methods.
.
Figure 2: Type I error for case 1.
F: for the fixed margin, S: for the synthesis margin. The significance level is 0.025 for NI approach but is 0.05 for both equivalence and cNI approaches.
View Figure 2
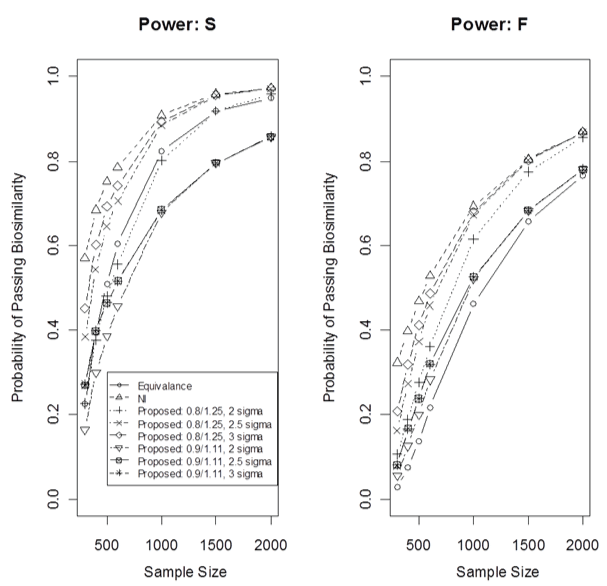
Figure 3 shows the power in case 2 for three methods using both the fixed and the synthesis approaches, where again the proposed cNI approach had three different k values in the PI and two different mean boundaries. As the sample size in the current biosimilar trial increases, the power increases. In general, the synthesis approach gives better power than the fixed margin approach. As expected, the non-inferiority approach gives the best power and the equivalence method has a much lower power at the same fixed sample size. However, the proposed cNI approach with k = 3 and the boundary 0.8/1.25 has a very comparative power comparing to the non-inferiority approach. Note that the cNI approach has an extra similarity condition for the clinical endpoint in addition to the non-inferiority. Thus, proposed cNI approach with certain k-value and the boundaries can perform very well. When the sample size is big enough, the cNI and the non-inferiority methods give similar power. Figure 3 also indicates that if an additional 5% to 10% sample size is added for the cNI approach, the cNI will have the same or more power than the non-inferiority approach. Thus, with an additional 5% to 10% sample size based on the sample size calculation for the non-inferiority design, the proposed cNI design should achieve the same or higher power comparing to the non-inferiority design.
.
Figure 3: Power comparison for different methods for case 2.
F: for the fixed margin, S: for the synthesis margin.
View Figure 3
Figure 4 displays the type I error in case 3 for three methods using both the fixed and the synthesis approaches, where again the proposed cNI approach had three different k values in the PI and two different mean boundaries. The probability of passing biosimilarity on the left side of the y-axis is for the equivalence and cNI approaches while the value in the right side of the y-axis is for the NI approach. In case 3, the T is better than R so, T & R are not similar. Whether this implies T should not be approved as a biosimilar is a topic for debate. Both the equivalence approach and the proposed cNI approach controlled the type I error well, where different constraints level can lead to different degree of type I error control. The non-inferiority method either doesn't control the type I error or demonstrates better power depending on one's perspective. However, the proposed cNI approach does not have this conflicting controversial issue.
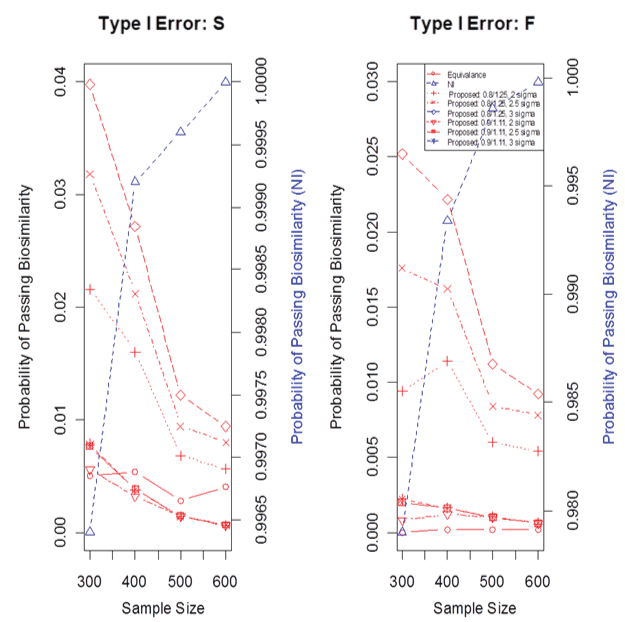
.
Figure 4: Type I error for case 3.
F: for the fixed margin, S: for the synthesis margin. The value on the left side of the y-axis is for the equivalence and cNI approaches while the value in the right side of the y-axis is for the NI approach.
View Figure 4
In summary, the non-inferiority approach requires smaller sample size and it can address the clinical efficacy of the biosimilar product but can fail the similarity to the reference product, while the equivalence approach can address both the clinical efficacy of the biosimilar product and the similarity to the reference product, but it requires larger sample size. However, the proposed cNI approach with carefully selected constraint can address both the clinical efficacy of the biosimilar product and the similarity to the reference product using the similar sample size required by the non-inferiority approach. In simulation, it seems that the k = 3 for constructing PI and 0.8/1.25 as the boundaries for the point estimate of the treatment effect are good choice for the cNI approach. Note that it is recommended to involve clinician for a thorough discussion to ensure this boundary is clinical meaningful and acceptable after the simulation assessment using the available information/data.
Illustrations
Consider two examples. The first dataset is the trial dataset from Snapinn and Jiang [2008b] [13]. In this trial, the standard reference treatment was approved based on a set of placebo-controlled trials in which a total of 100 of 1000 placebo subjects with a prespecified unfavorable event and thus, the smaller the "event", the better efficacy of the product, and 74 of 1000 reference product treated subjects with the "event". Suppose a current biosimilar trial is conducted with the same population where a total of 90 of 1200 reference product treated subjects with the "event", and 77 of 1200 proposed biosimilar product treated subjects with the "event". The data are shown as dataset 1 in table 1. The second dataset is a minor modification of the dataset 1. The only difference is a reduction of the total "event" from the proposed biosimilar product treatment from 77 to 65; thus, the proposed biosimilar product is more efficacious.
![]()
Table 1: Two mock datasets.
View Table 1
Following Snapinn and Jiang [2008b], the negative log-odds ratio will be used as the analysis variable to evaluate the treatment effect in order to satisfy the criteria that the analysis variable has an approximately normal distribution and that greater values represented better efficacy [13]. Using the data from the historical placebo controlled trial results in BRP and VRP = 0.0213. For evaluation of all three approaches, a 50% effect preservation, f = 0.5, is used. For the proposed cNI approach as an illustration, k = 3 is used for constructing the PI and 0.8/1.25 are used as the boundaries for the point estimate of the odds ratio.
For dataset 1, the data from the current biosimilar trial results in and Using the fixed-margin approach, and . Thus, both the non-inferiority and the equivalence methods reject the biosimilarity conclusion using the fixed margin approach. Using the synthesis-margin approach, and . Thus, both the non-inferiority and the equivalence methods also reject the biosimilarity conclusion using the synthesis margin approach. The odds ratio of the proposed biosimilar product relative to the reference product is 0.846 and the 95% confidence interval of the odds ratio is (0.617, 1.159). Using both the reference data from both the historical placebo-controlled trial and the current biosimilar trial, is calculated for the log-odds ratio. Thus, the PI for the odds ratio is (0.612, 1.634). Since (0.617, 1.159) is within the PI (0.612, 1.634) and the 0.846 is within 0.8/1.25, therefore, T and R have comparable distributions in terms of the odds ratio. However, the NI approach showed that biosimilar product lack of efficacy for both the fixed margin and the synthesis margin approaches. Thus, the proposed cNI approach would also reject the biosimilar conclusion using both the fixed margin and the synthesis approach. In summary, all three methods have the same conclusion. The results using different methods are summarized in table 2.
![]()
Table 2: Statistical results for the two mock datasets using effect preservation f = 0.5.
View Table 2
For dataset 2, only changes were the data for the test biosimilar product in the current biosimilar trial and the data from the current biosimilar trial results in and . Again, a 50% effect preservation, f = 0.5, is used. Using the fixed-margin approach, and . Thus, the non-inferiority method would not reject the biosimilarity conclusion but the equivalence method would reject the biosimilarity conclusion using the fixed margin approach. Using the synthesis-margin approach, and . Thus, the synthesis method also yields the same conclusions. The odds ratio of the proposed biosimilar product relative to the reference product is 0.706 and the 95% confidence interval of the odds ratio is (0.508, 0.982). Since the reference data are the same in dataset 2 as in dataset 1, for the log-odds ratio. Thus, the PI for the odds ratio is (0.612, 1.634). Since the (0.508, 0.982) is outside the PI (0.612, 1.634) and the 0.706 is outside 0.8/1.25, therefore, T and R are not deemed to have comparable distributions in terms of the odds ratio and the proposed cNI approach would reject the biosimilarity conclusion even though the T is certainly efficacious and superior to the placebo from the NI approach for both the fixed margin and the synthesis margin approaches. In summary, the equivalence approach and the cNI methods reject the biosimilarity conclusion while the traditional non-inferiority approach fails to reject the biosimilarity conclusion. The cNI rejects the biosimilarity due to the similarity issue, not due to the efficacy. The results for dataset 2 using different methods are also summarized in table 2.
Summary
There are tremendous scientific and statistical challenges and opportunities in developing biosimilars. It is a stepwise approach and what we know at current stage determines what to do next. The approvability of biosimilars depends on the totality of evidence with the use of fingerprint-like techniques for extensive characterization. Direct head to head comparison between the biosimilars and the reference begins with the in vivo and in vitro critical quality attributes, and ends with the clinical efficacy comparison to assess the residual uncertainty of the biosimilarity.
In this paper, a cNI approach was proposed and compared with non-inferiority and equivalence approaches. An equivalence approach usually requires much larger sample size to achieve the same power as the non-inferiority approach, but the non-inferiority approach only guarantees that the test product is not inferior to the reference product and thus, may pass a product with increased activity compared to the reference product. However, the cNI approach, which addresses both the clinical efficacy of the biosimilar product and the similarity to the reference product, was shown in the simulation study to have better performance than the equivalence approach in terms of the power, while maintaining type I error. Predictably, the approach has somewhat less power than the straight non-inferiority approach as some evidence supporting that the test is not appreciably more efficacious than the reference is required. The cNI approach uses the traditional non-inferiority plus a plausibility interval and a point estimate criteria, where the extra requirements and the constraints serve as the supporting evidence that the test is not appreciably more efficacious than the reference. All these factors could be predetermined with the consensus from the health authorities. The information from comparing the reference against the reference itself is used as the goalpost to set up the biosimilarity plausibility interval. To achieve this, the information from current biosimilar trial may be borrowed through the interim analysis or after the trial finalization. Since many parameters are involved in the proposed cNI approach, a more conservative conclusion can be achieved if needed. The type I error can be easily controlled through different combinations of parameters, and it seems that the k = 3 for constructing the PI and 0.8/1.25 as the boundaries for the point estimate of the treatment effect are good choices for the cNI approach. However, it is recommended that simulations be performed for every trial to justify the type I error control. An additional 5% to 10% sample size than that based on the sample size calculation for a straightforward non-inferiority design is recommended so that the proposed cNI design and analysis would achieve the similar power.
The proposed cNI approach had good performance in the simulation study and the examples in terms of power and type I error control and suggests promise for this approach. The information from comparing the reference to the reference itself can be used as the goalposts for setting the acceptance criteria. In summary, the proposed cNI approach generally requires smaller sample sizes than that from an equivalence approach but meets all necessary requirements addressing biosimilarity for efficacy trials, which can make the difference in development costs that determine the economic viability of biosimilar projects.
Disclaimers
The thoughts and opinions presented in this paper only represent the author's positions.
Acknowledgements
The author thanks the editor and a referee for their valuable comments that improved the presentation of this paper. The author also wants to thank the former and current colleagues for many discussions and suggestions on different versions of this paper.
References
-
(2013) Genetic Engineering & Biotechnology News (GEN). Top 20 Best-Selling Drugs of 2012.
-
(2014) Genetic Engineering & Biotechnology News (GEN). The Top 25 Best-Selling Drugs of 2013.
-
(2015) Genetic Engineering & Biotechnology News (GEN). The Top 25 Best-Selling Drugs of 2014.
-
(2013) Generic Pharmaceutical Association (GPA). Generic Drug Savings in the US. Fourth Annual Edition: 2012.
-
(2012a) Food and Drug Administration (FDA) of USA. Guidance for industry: Scientific considerations in demonstrating biosimilarity to a reference product. Washington, D.C.
-
(2012b) Food and Drug Administration (FDA) of USA. Guidance for industry: Quality considerations in demonstrating biosimilarity to a reference product. Washington, D.C.
-
(2012c) Food and Drug Administration (FDA) of USA. Guidance for industry: Biosimilars: Questions and answers regarding implementation of the biologics price competition and innovation act of 2009. Washington, D.C.
-
(2009) World Health Organization (WHO). Guidelines on evaluation of similar biotherapeutic products (SBPs), Geneva.
-
(2005) EMEA Committee for Medicinal Products for Human Use (CHMP). Guideline on similar biological medicinal products, London.
-
Liao JJZ, Heyse JF (2011) Biosimilarity for follow-on biologics. Statistics in Biopharmaceutical Research 3: 445-455.
-
Babbitt B, Nick C (2011) Considerations in establishing a US approval pathway for biosimilar and interchangeable biological products. DIA Global Forum 3: 44-49.
-
Snapinn S, Jiang Q (2008) Controlling the type 1 error rate in non-inferiority trials. Stat Med 27: 371-381.
-
Snapinn S, Jiang Q (2008b) Preservation of effect and the regulatory approval of new treatments on the basis of non-inferiority trials. Statistics in Medicine 27: 382-391.
-
Rothmann M, Li N, Chen G, Chi GY, Temple R, et al. (2003) Design and analysis of non-inferiority mortality trials in oncology. Stat Med 22: 239-264.
-
(2005) Special Issue: Therapeutic Equivalence - Clinical Issues and Statistical Methodology in Noninferiority Trials, Biometrical Journal 47: 5-107.
-
(2010) Food and Drug Administration (FDA) of USA. Guidance for industry: non-inferiority clinical trials. Washington, DC.
-
Chow SC, Endrenyi L, Lachenbruch PA (2013) Comments on the FDA draft guidance on biosimilar products. Stat Med 32: 364-369.
-
Liao JJ, Darken PF (2013) Comparability of critical quality attributes for establishing biosimilarity. Stat Med 32: 462-469.