International Journal of Neurology and Neurotherapy
Effect of Elasticity on Flow Characteristics Inside Intracranial Aneurysms
Ryuhei Yamaguchi*, Gaku Tanaka and Hao Liu
Graduate School of Engineering, Chiba University, Japan
*Corresponding author:
Ryuhei Yamaguchi, Graduate School of Engineering, Chiba University, 1-33 Yayoi-cho, Inage-ku, Chiba 263-8522, Japan, Tel: +81 43 251-1111 ext.4538, E-mail: yryuhei63@gmail.com
Int J Neurol Neurother, IJNN-3-049, (Volume 3, Issue 3), Review Article; ISSN: 2378-3001
Received: April 28, 2016 | Accepted: May 23, 2016 | Published: May 25, 2016
Citation: Yamaguchi R, Tanaka G, Liu H (2016) Effect of Elasticity on Flow Characteristics Inside Intracranial Aneurysms. Int J Neurol Neurother 3:049. 10.23937/2378-3001/3/3/1049
Copyright: © 2016 Yamaguchi R, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
Many medical and bioengineering researchers have investigated flow behavior inside intracranial aneurysms using computational fluid dynamics. The majority of these studies assume to be rigid wall, but blood flows through a deformable elastic vessel. A few researchers have tried to simulate using fluid-structure interaction because an elastic wall implicates the decrease of wall shear stress inside the aneurysms. The current experimental model with the elastic wall has been carried out using particle image velocimetry. Comparing of wall shear stress in elastic wall aneurysm with that in rigid one, it is clarified that the wall shear stress in elastic wall is approximately 7% smaller than that in rigid one. Although this reduction is small, it affects the flow instability which is very sensitive. This behavior might also influence the spatial gradient of wall shear stress. Recently, the high magnitude and the positive gradient of wall shear stress are regarded to initiate at the apex the aneurysms. In this review, the importance of wall shear stress is described. We also look at how the wall deformation affects the flow characteristics in computational fluid dynamics inside the intracranial aneurysms prospectively.
Keywords
Intracranial aneurysm, Elasticity, Wall shear stress, Flow instability
Introduction
"Circle of Willis" is composed of many vessels and bifurcations. The anterior communicating, middle cerebral, basilar and carotid arteries are regarded as the typical predilection vessels of intracranial aneurysms.
Intracranial aneurysms initiate and develop at specific cerebrovascular sites closely associated with hemodynamic factors. Recently, the hemodynamics of aneurysm have been extensively investigated using computational fluid dynamics (CFD) [1,2]. Furthermore, the flow behavior has also been measured using particle imaging velocimetry (PIV) in patient-specific aneurysm models [3-5]. However, in the majority of recent studies the vascular wall is assumed to be rigid in CFD.
In recent decades, many retrospective studies have been carried out to investigate the hemodynamic difference of ruptured and unruptured aneurysms with the advancement of CFD. The hemodynamic factors, including wall shear stress (WSS), oscillatory shear index (OSI), impingement regions, inflow jet, pressure loss coefficient and flow instability, have been indicated as indicators for the rupture risk [2,4,6-9]. A total of more than 200 ruptured and unruptured aneurysms were analyzed in CFD and showed that morphology played an important factor of hemodynamics in discriminating aneurysm rupture status [2,4,7]. However, the risk factors and the rupture mechanism of intracranial aneurysms have not been clarified yet.
Experiments by PIV have been performed to validate the velocity fields calculated in CFD for patient-specific aneurysms. They showed that velocity vector in PIV agreed with that in CFD, but gross flow patterns and detailed flow structures cannot exactly clarify in CFD [3,10].
An intracranial aneurysm consists of thin elastic wall. Vascular disease is related to flow field in the vicinity of the aneurysms and WSS acting on the aneurysm wall would affect the initiation of vascular disease. Therefore, the effect of wall elasticity on WSS should be clarified by both experiment and simulation. With respect to the elastic intracranial aneurysms, the fluid-structure interaction (FSI) of blood flow has been carried out to investigate the influence of the elastic wall on the hemodynamic factors [11]. Currently, WSS reduction in an elastic aneurysm wall is indicated in an idealized spherical aneurysm model by both PIV and FSI [12,13]. Owing to the lack of suitable experimental techniques, it is not easy to verify the validation of FSI results. A few studies compared CFD results with experiments, which used in vivo and in vitro phase contrast MRI to validate the CFD flow simulations: they proved CFD to be useful in modeling hemodynamic factors [14].
Recently, it has been suggested that the high magnitude and the positive spatial gradient of wall shear stress (WSSG) affects the initiation of aneurysm [8,15]. The positive WSSG might affect the development and the rupture of the aneurysm. With regard to the effects of WSS on endothelial cells (ECs) function, it was indicated that ECs use multiple sensing mechanisms to detect changes in mechanical forces and can respond differently to laminar, disturbed and oscillatory flow [16,17].
WSS reduction might be associated with the response of ECs and the release of hemodynamic force against the intima exposed to WSS. The presence of bruits with a phonocatheter from the sacs of 10 intracranial aneurysms with dominant frequency of 460 Hz1 ± 30 was detected [18]. So, WSS reduction might affect prospective research, e.g. flow instability inside the aneurysms [9].
Elasticity for Flow Characteristics
The majority of medical and bioengineering researchers have been investigating in CFD with the assumption of a rigid aneurysm wall. Although the WSS reduction was indicated in a FSI simulation and the elasticity has an important effect on WSS, no one endorses the degree of WSS reduction experimentally except for few studies [12,13].
Clinically, the deformation ratio of intracranial aneurysm was 3-8 % with respect to diameter in phase contrast magnetic resonance imaging [19]. Although its ratio might be small, the effect of elasticity on flow characteristics would be impossible to ignore.

.
Figure 2: Velocity vector inside elastic model in sinusoidal flow wave (Re = 435, α = 4.0)
(a) PIV, (b) CFD
View Figure 2
Suppression of Wall Shear Stress by Elasticity
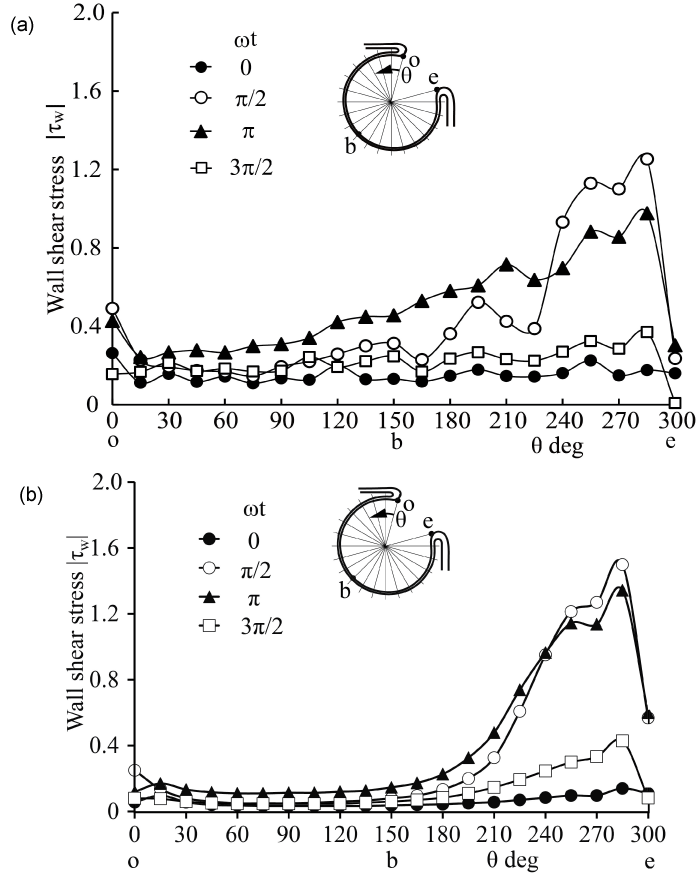
Currently, it is not easy to simulate a patient-specific full-scale phantom model because the size of an intracranial aneurysm is generally 5 to 10 mm with very thin wall. In the 3.6-fold scaled-up idealized spherical elastic aneurysm model induced at the bifurcation of anterior communicating artery in figure 1 [12], the velocity behavior are indicated in sinusoidal flow wave at the inlet in Re = 435 and α = 4.0 in figure 2. The Reynolds number is defined as Re = Ud0/ν where U and d0 are mean velocity and diameter in afferent vessel, respectively and ν is kinematic viscosity of working fluid. The Womersley number is also defined as α = (d0/2)(ω/ν)(1/2) where ω is angular velocity of pulsating frequency. The magnitude of WSS and the spatially temporal averaged WSS in elastic wall reduced comparing with those in rigid wall in figure 3 and figure 4. At peak systole, the maximum WSS in elastic model is 30% lower than that in rigid model. Furthermore, the spatial and temporal averaged value of WSS in elastic model is approximately 7% smaller than that in rigid one by PIV and FSI.
.
Figure 3: WSS along elastic aneurysm wall in PIV and CFD (Re = 435, α = 4.0)
(a) PIV, (b) CFD
View Figure 3
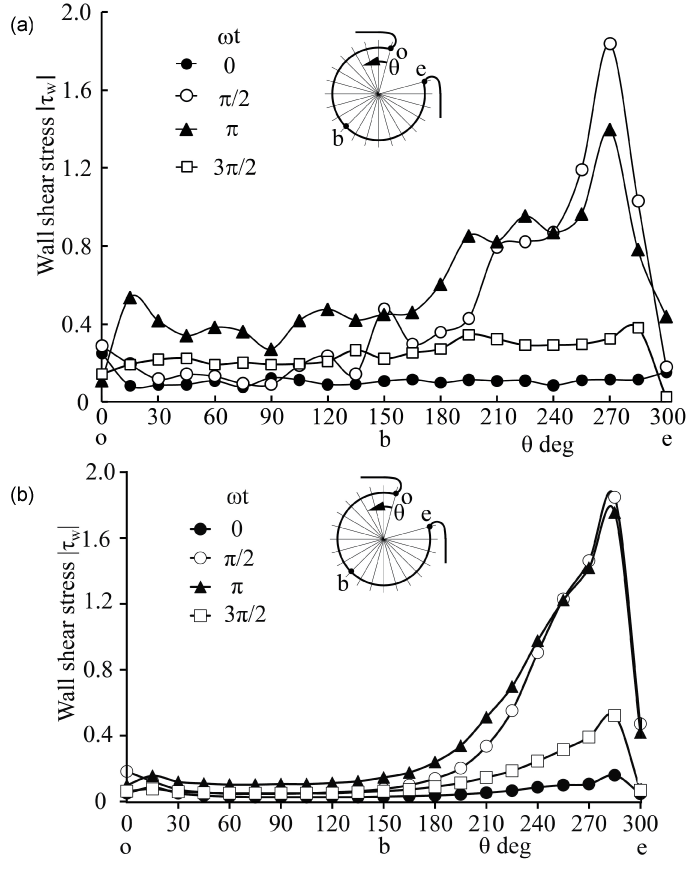
.
Figure 4: WSS along rigid aneurysm wall in PIV and CFD (Re = 435, α = 4.0)
(a) PIV, (b) CFD
View Figure 4
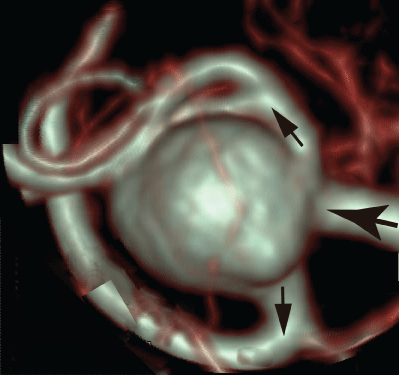
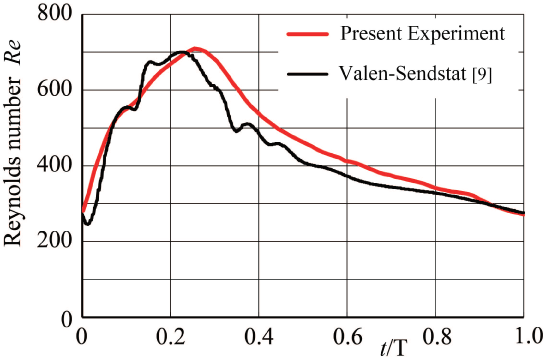
To reconfirm the above results, the patient-specific image in figure 5 has been referred as the aneurysm model at the bifurcation of middle cerebral artery [13]. Although the morphology is similar to the former model, the flow condition simulates the physiological pulsatile blood flow wave and α = 1.41 in figure 6 [9,13]. This model deformed 4.7% with respect to the diameter of aneurysm corresponding to clinical results [19]. Velocity and WSS (τW) were experimentally examined in the middle cerebral aneurysm in figure 7 and figure 8, respectively. Overall, although the velocity at peak systole in the elastic model is slightly larger than that in the rigid model, the volume dilatation of 115 % in an elastic wall would be closely related to lower WSS. This spatial and temporal averaged value of WSS in elastic model is approximately 7% lower than that in rigid model. This averaged WSS reduction coincides with the former case despite the different Womersley number. Therefore, the wall elasticity suppresses the magnitude of WSS as indicated in the former flow condition.
Currently, the wall of intracranial aneurysms is assumed to be rigid and the effect of elasticity is little for flow behaviors, i.e. OSI, WSS and flow instability. However, it is implicated that this WSS reduction by the deformability in the intracranial aneurysms should consider elasticity.
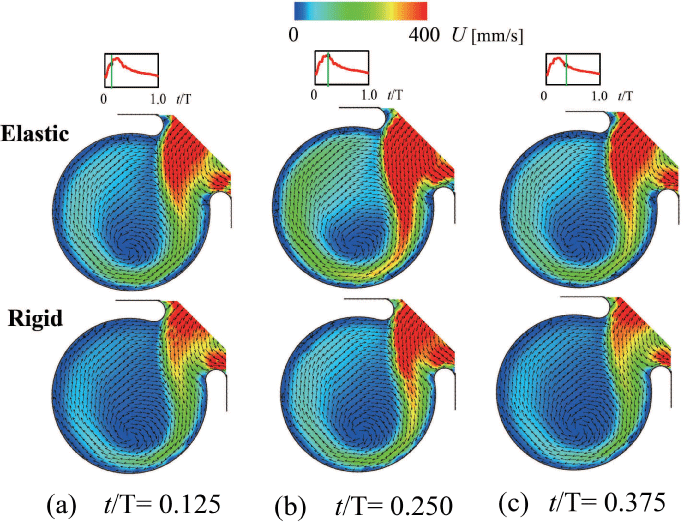
.
Figure 7: Velocity vector inside elastic and rigid models (Re = 460, α = 1.41)
(a) t/T = 0.125 (Early systole), (b) t/T = 0.250 (Peak systole), (c) t/T = 0.375 (Mid-diastole)
View Figure 7
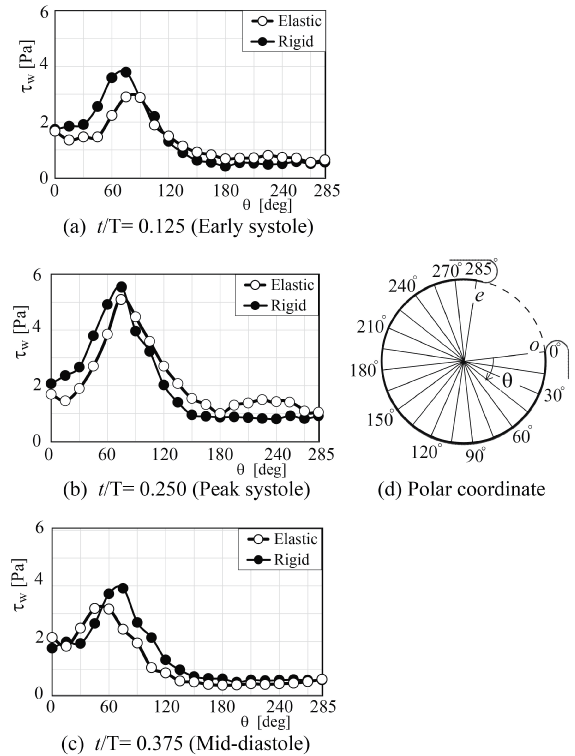
.
Figure 8: WSS along elastic and rigid aneurysm walls (Re = 460, αl; = 1.41)
(a) t/T = 0.125 (Early systole), (b) t/T = 0.250 (Peak systole), (c) t/T = 0.375 (Mid-diastole), (d) Polar coordinate
View Figure 8
Behavior of Flow Instability
Recently, flow instability was extensively noticed as one of risk factors of aneurysm growth and rupture using patient-specific models. It is sure that the flow instability was clarified in the intracranial aneurysms [18].
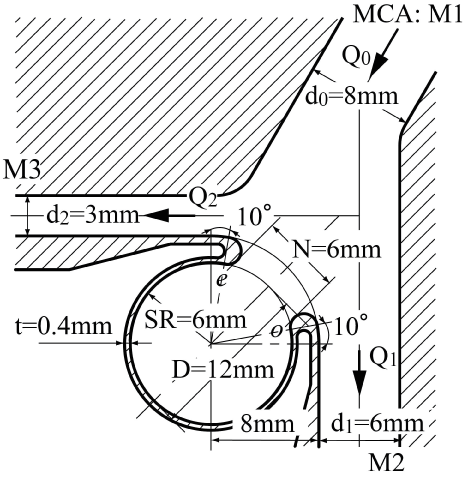
This flow instability is very sensitive and sometimes induces the periodic oscillation. The periodic vibration accompanying flow instability in the side branch of a T-junction has been indicated in laminar steady flow at Re = UT d0/ν = 800 in trunk in figure 9 [20] where UT and d0 are mean velocity and diameter in trunk, respectively. In the side branch, the tangential velocity profile across the shearing separation layer has a high shear rate of 80 s-1 against shear rate of 24 s-1 at tube wall sufficiently downstream of the side branch in figure 9(b). At point P1, the tangential velocity profile across this layer indicates the clear inflection point with high shear rate. In side branch, the periodic oscillation appears from Re = 300 to 900. Emphasizing flow instability and oscillation, the magnitude of shear rate and the existence of inflection point should be indicated. Even if the effect of elasticity is very small inside the aneurysms, there would be some influences of the elasticity on flow behavior.
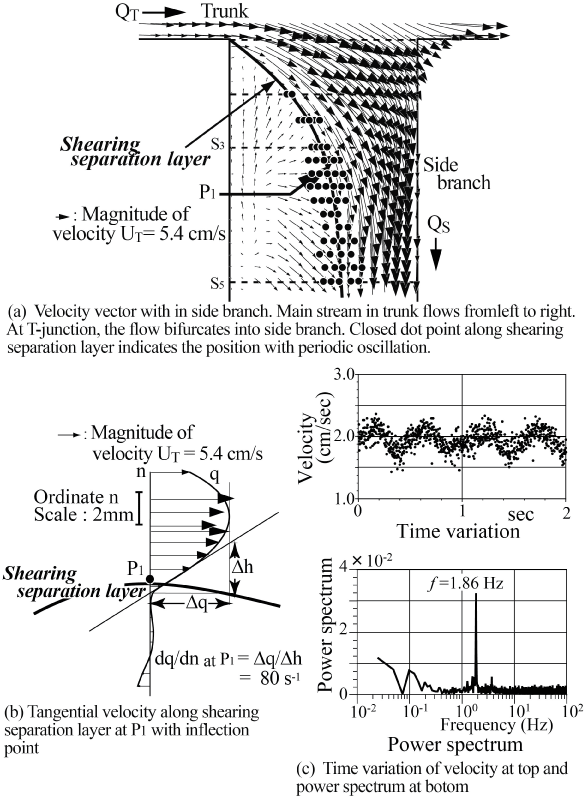
.
Figure 9: High shear rate flow with inflection point within side branch of T-Junction.
(Re = UTD/v = 760 where UT and D are mean velocity and diameter in trunk, respectively, flow division ratio of QS/QT = 0.23, the shear rate is 24 s-1 at tube wall sufficiently downstream of side branch.)
(a) Velocity vector within side branch. Main stream in trunk flows from left to right. At T-junction, the flow bifurcates into side branch. Closed dot point along shearing separation layer denotes the position with periodic oscillation;
(b) Tangential velocity along shearing separation layer at P1 with inflection point;
(c) Time variation of velocity at top and power spectrum at bottom.
View Figure 9
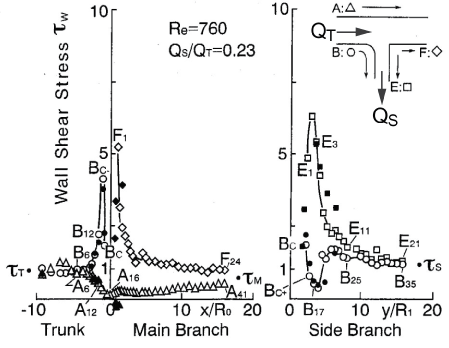
.
Figure 10: Distribution of WSS in T-Junction around round inlet corner.
(Re = 760, flow division ratio of QS/QT = 0.23. Open and closed symbols were measured by electrochemical method and laser Doppler velocimetry, respectively. Origin 0 is the bifurcation point.)
View Figure 10
Spatial Gradient of Wall Shear Stress
For three decades, it has been suggested that atherosclerosis is initiated at sites with low WSS or OSI≠0, such as the separation region. As the predilection site of atherosclerosis, the bifurcation from the abdominal aorta to renal artery was often examined. Generally, the separation flow was regarded to appear immediately downstream of the round inlet of side branch. However, in the right-angle simulating to renal artery from abdominal artery in laminar steady flow, there is no separation, low WSS and negative WSSG in figure 10 [21]. WSS (τW) around the round inlet of side branch denoted by circle symbol ○ along the proximal wall B in figure 10 decreases, but WSS is not negative. The atherosclerosis is apt to initiate along wall B, i.e. circle symbol ○, around round inlet corner of side branch. WSS (τW) is small positive immediately downstream of round corner. The characteristic feature in the bifurcation is negative WSSG. In figure 11, the physiological meaning of negative WSSG in figure 11(b) is similar to the separation flow [22]. It was indicated that OSI≠0 has the same physiological meaning as negative WSSG which corresponds to separation or divergent flows in figure 12, i.e. "Compression for ECs", and the initiation of atherosclerosis is related to it. In other words, it is not necessarily to be OSI≠0 when WSSG is negative.
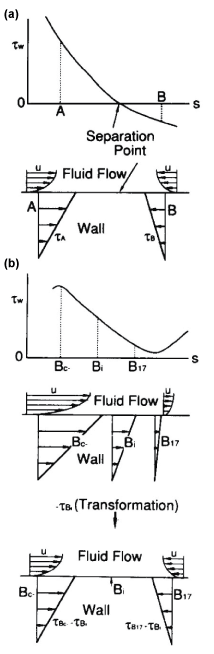
.
Figure 11: Physiological meanings of negative WSSG.
(a) Separation flow with OSI ≠ 0;
(b) No separation flow with negative WSSG of WSS > 0 and OSI = 0
View Figure 11
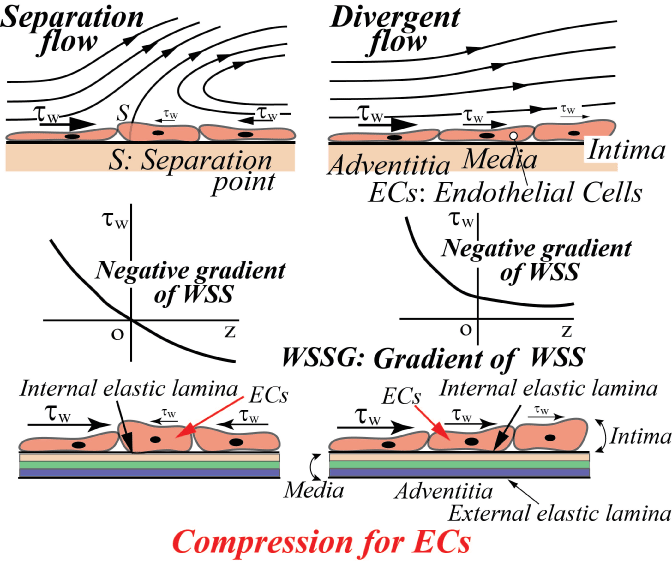
.
Figure 12: Effect of negative gradient of WSS on ECs (Negative WSSG affects the compression for ECs).
View Figure 12
On the contrary, the intracranial aneurysms are apt to initiate at the apex of bifurcation [15]. Normally, WSS is zero or very low at the apex and steeply increases downstream, i.e. the spatial gradient of WSS is positive. The reattachment flow has also the same physiological meaning as the convergent flow in figure 13, i.e. the positive WSSG corresponds to "Stretching for ECs" and is closely related to the initiation of intracranial aneurysms [15].
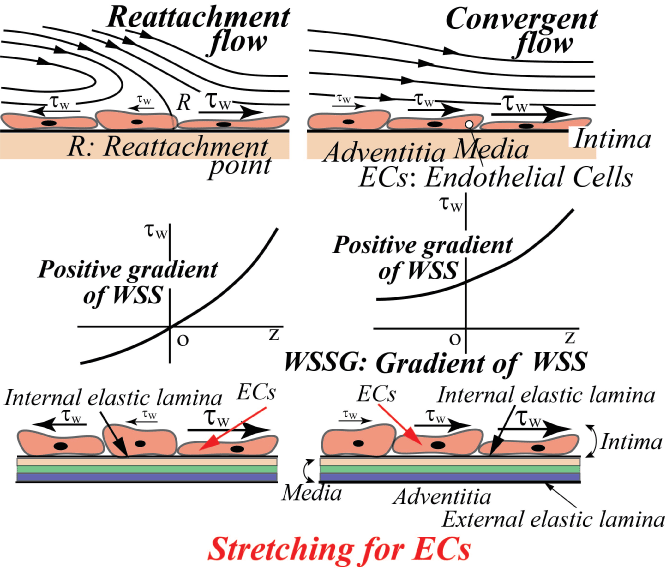
.
Figure 13: Effect of positive gradient of WSS on ECs (Positive WSSG affects the stretching for ECs.)
View Figure 13
Generally, the flow pattern of predilection site with respect to aneurysms is quite different from that concerning atherosclerosis. WSS is the gradient of tangential velocity along the aneurysm wall and is very sensitive. Essentially, WSSG which is the derivative with respect to flow direction of WSS would be influenced by a little wall displacement accompanying the deformation by the elasticity. So, the spatial gradient of WSS includes an important pathological meaning. Furthermore, the elasticity might affect WSSG acting on vascular endothelium.
Remarks
Numerical simulation of the intracranial aneurysms should take elasticity into account. With regard to WSSG and flow instability inside aneurysm dome, there would be some influences of the elasticity in CFD.
References
-
Sforza DM, Putman CM, Cebral JR (2009) Hemodynamics of Cerebral Aneurysms. Annu Rev Fluid Mech 41: 91-107.
-
Takao H, Murayama Y, Otsuka S, Qian Y, Mohamed A, et al. (2012) Hemodynamic differences between unruptured and ruptured intracranial aneurysms during observation. Stroke 43: 1436-1439.
-
Ford MD, Nikolov HN, Milner JS, Lownie SP, Demont EM, et al. (2008) PIV-measured versus CFD-predicted flow dynamics in anatomically realistic cerebral aneurysm models. J Biomech Eng 130: 021015-1/9.
-
Xiang J, Natarajan SK, Tremmel M, Ma D, Mocco J, et al. (2011) Hemodynamic-morphologic discriminants for intracranial aneurysm rupture. Stroke 42: 144-152.
-
Yamaguchi R, Ujiie H, Haida S, Nakazawa N, Hori T (2008) Velocity profile and wall shear stress of saccular aneurysms at the anterior communicating artery. Heart Vessels 23: 60-66.
-
Dhar S, Tremmel M, Mocco J, Kim M, Yamamoto J, et al. (2008) Morphology Parameters for Intracranial Aneurysm Rupture Risk Assessment. Neurosurgery 63: 185-197.
-
Sforza DM, Putman CM, Cebral JR (2009) Hemodynamics of Cerebral Aneurysms. Annu Rev Fluid Mech 41: 91-107.
-
Meng H, Wang Z, Hoi Y, Gao L, Metaxa E, et al. (2007) Complex hemodynamics at the apex of arterial bifurcation induces vascular remodeling resembling cerebral aneurysm initiation. Stroke 38: 1924-1931.
-
Valen-Sendstad K, Mardal KA, Mortensen M, Reif BAP, Langtangen HP (2011) Direct numerical simulation of transitional flow in a patient-specific intracranial aneurysm. J Biomech 44: 2826-2832.
-
Raschi M, Mut F, Byrne G, Putman CM, Tateshima S, et al. (2012) CFD and PIV analysis of hemodynamics in a growing intracranial aneurysm. Int J Numer Method Biomed Eng 28: 214-228.
-
Torii R, Oshima M, Kobayashi T, Takagi K, Tezduyar TE (2010) Influence of wall thickness on fluid–structure interaction computations of cerebral aneurysms. Inter J Num Meth in Biomed Eng 26: 336-347.
-
Xu L, Sugawara M, Tanaka G, Ohta M, Liu H, et al. (2016) Effect of elasticity on wall shear stress inside cerebral aneurysm at anterior cerebral artery. Tech & Health Care.
-
Tanaka G, Yamaguchi R, Omachi S, Saito A, Liu H (2016) Experimental study of elasticity on flow pattern and wall shear stress inside middle cerebral aneurysm. J Biomech.
-
Acevedo-Bolton G, Jou LD, Dispensa BP, Lawton MT, Higashida RT, et al. (2006) Estimating the hemodynamic impact of interventional treatments of aneurysms: numerical simulation with experimental validation: technical case report. Neurosurgery 59: E429-430.
-
Dolan JM, Kolega J, Meng H (2013) High wall shear stress and spatial gradients in vascular pathology: a review. Ann Biomed Eng 41: 1411-1427.
-
Li YS, Haga JH, Chien S (2005) Molecular basis of the effects of shear stress on vascular endothelial cells. J Biomech 38: 1949-1971.
-
Himburg HA, Dowd SE, Friedman MH (2007) Frequency-dependent response of the vascular endothelium to pulsatile shear stress. Am J Physiol Heart Circ Physiol 293: H645-653.
-
Ferguson GG (1970) Turbulence in human intracranial saccular aneurysms. J Neurosurg 33: 485-497.
-
Meyer FB, Huston J, Riederer SS (1993) Pulsatile increases in aneurysm size determined by cine phase-contrast MR angiography. J Neurosurg 78: 879-883.
-
Tanaka G, Yamaguchi R, Liu H, Hayase T (2016) Fluid vibration induced by high-shear-rate in a T-Junction. ASME J. Fluid Engineering.
-
Fujii H, Yamaguchi R, Tanishita K (2005) Distribution of wall shear stress in right-angle branches during laminar flow. JSME Int Journal 48: 468-473.
-
Yamaguchi R, Nishida M, Nakaya N (1994) Effect of geometrical shape of side branch and flow condition on wall shear stress in right angle branch. Trans. JSME 60: 56-62.