International Journal of Radiology and Imaging Technology
Alternative Mathematical Form for Determining the Effectiveness of High-LET Radiations at Lower Doses Region
Abubaker Ali Yousif Alghoul1* and Muhamad Samudi Yasir2
1Department of Physics, Faculty of Science, Sebha University, Sebha, Libya
2School of Applied Physics, Faculty of Science and Technology, University Kebangsaan Malaysia, Malaysia
*Corresponding author:
Abubaker A. Yousif , Department of Physics, Faculty of Science, Sebha University, Sebha, Libya, Tel: +218-91695-7760, E-mail: alghoul75@yahoo.com
Int J Radiol Imaging Technol, IJRIT-2-009, (Volume 2, Issue 1), Original Article
Received: January 23, 2016: Accepted: March 28, 2016: Published: March 30, 2016
Citation: Alghoul AAY, Yasir MS (2016) Alternative Mathematical Form for Determining the Effectiveness of High-LET Radiations at Lower Doses Region. Int J Radiol Imaging Technol 2:009
Copyright: © 2016 Alghoul AAY, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
The Effectiveness of lower doses of high-LET radiations is not accurately determined by using energy-based physical parameters such as absorbed dose and radio-sensitivity parameters. Therefore, an attempt has been carried out in this research to propose alternative parameter that capable to quantify the effectiveness of these high LET radiations at lower doses regions. The linear energy transfer and mean free path for linear primary ionization are employed as distinct parameters to achieve this objective. A new mathematical form of the effectiveness of high-LET radiations at lower doses region has been formulated. Based on this parameter, the optimized effectiveness of high-LET radiations occurs while the energy of higher LET particles is deposited at spacing of 2 nm for linear primary ionizations.
Keywords
Effectiveness, Low dose, Radiation mean free path, Linear energy transfer
Introduction
Investigating the effectiveness of high-LET radiations on biological systems is one of most significant aims in the fields of radiation research and radiation protection [1]. However, it is well known that the amount of energy transferred to biological entities, from high-LET radiations, is quantified in terms of physical quantities, which are defined based on radiation energy [2].
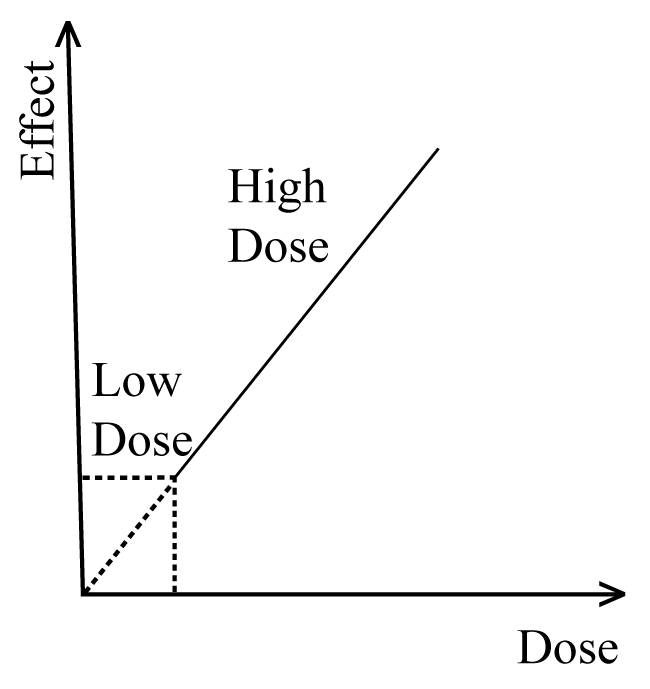
Currently, in radiation protection field, the effectiveness of high-LET radiations is determining in terms of absorbed dose as a significant physical parameter. The absorbed dose is typically defined as the amount of energy deposited by charged particles per unit volume of the irradiated medium. However defining the absorbed dose in this form allows to using it as a typical physical quantity in determine the effectiveness of high-LET radiations on physical materials. Although the absorbed dose as a distinct parameter was applied effectively to quantify the effectiveness of high-LET radiations in biological materials at higher doses region. Conversely, at lower doses region, this parameter faces major insignificance in quantifying the effectiveness in finite biological entities such as cells, chromosomes and DNA molecules, as shown in figure 1. Whereas the effectiveness of high-LET radiations is predicted using extrapolated methods. There is another weakness of using the absorbed dose as distinct parameter which is related to the fact that the absorbed dose does not consider spatial distribution of deposited energy by charged particles. The spatial distribution explains the exact relationship between the radiation effectiveness and the radiation energy imparted by high-LET radiations at lower doses region [3].
.
Figure 1: The connected line shows the high dose region while the dotty line shows low dose region.
View Figure 1
However to look into these problems and to address the weaknesses of using the absorbed dose as a distinct physical quantifier parameter to determine the radiation effectiveness, the concept of relative effectiveness of radiations has been introduced. The relative biological effectiveness (RBE) of radiations introduced to compare the effectiveness produced by various qualities of high-LET radiations. In fact, the equal amounts of the absorbed doses from varies qualities of high-LET radiations do not create the same biological effect level.
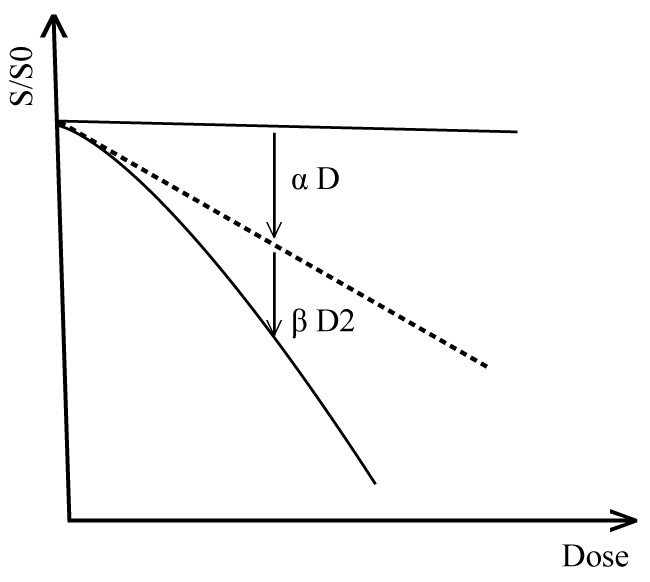
It has been realized that in many studies; the absorbed dose is not the optimum physical parameter to quantify the effectiveness of high-LET radiations at lower doses [3-7]. For that reason the radio-sensitivity of cell survival curves have been applied to determine the effectiveness of high-LET radiations at this region [8] as shown in figure 2 for Linear-Quadratic model.
.
Figure 2: The αD represents the inactivated fraction of irradiated cells at lower doses and the βD2 represents the inactivated fraction of irradiated cells at higher doses region.
View Figure 2
For convenience, the effectiveness was defined as the ratio of initial slope of reference radiation (αr) to the initial slope of the test radiation (αt) as shown in figure represented below.
In radiation protection, this simple form of effectiveness faces a gross limitation, in particular while the initial slope of tested radiation approaches zero point. In this case, the effectiveness should also reach at zero; however, this fact is not proven yet. Consequently, the initial slopes parameters do not represent suitable quantifiers of high-LET radiation effectiveness at lower doses region. For that reason, investigating alternative physical parameters has been done in this research.
Since LET and its restricted forms are considered to be good physical quality parameters to quantify high-LET radiation damage [9], in fact it depends on mass and velocity of charged particles, as such, various values of linear energy transfer may be acquired either through changing the particle energy with the same particle or by altering the particle type keeping the velocity constant. Using the LET alone is not really good physical method to determine the radiation quality, which in turn leads to deduce that the effectiveness of high-LET radiations represented in this parameter is not accurately determined because of the serious limitation relevant to the RBE concept [10-12]. Furthermore Belli [13] has experimentally proven that the LET cannot be considered as a common index of radiation effectiveness for light particles. This implication was subsequently confirmed in many laboratories [13,14]. The possible method to rise above this limitation is that by representing the radiation quality in terms of two physical parameters at the same time. Thus the attention has been focused to derive an alternative form of the relative effectiveness in terms of two physical parameters rather than the absorbed doses, the initial slopes or the LET alone.
Derivation of Alternative Form of Effectiveness (RBE)
Definition of the effectiveness (RBE) has been introduced for the first time as the ratio of absorbed dose of a reference radiation to the absorbed dose of a test radiation which produces the same biological end-point. This definition of RBE was given mathematically as follows:
Where Dr is the absorbed dose from reference radiation and Dt represents the absorbed dose from test radiation.
On the other hand, at lower doses region, the relative biological effectiveness (RBE) may be represented in terms of the initial slopes of cell survival curves by the simple relation:
Where αr is the initial slope of survival curve of reference radiation and αt expresses the initial slope of survival curve of test radiation.
The effect cross-section (σ) which identify the target size of biological targets such as: cell, cell nucleus and DNA can be defined in terms of linear energy transfer (LET) as follows:
Where α represents the radio-sensitivity parameter which determines the effectiveness at low dose region, and LET represents the linear energy transfer parameter of charged particles. σ0 represents saturated cross-section.
For reference radiation we can write:
Where σr and αr represent the effect cross-section of survival curve and radio-sensitivity parameter of reference radiation respectively, LETr represents the linear energy transfer parameter of reference radiation.
For test radiation we have:
Where σt and αt represent the effect cross-section of survival curve and radio-sensitivity parameter of test radiation respectively, LETr represents the linear energy transfer parameter of test radiation.
From equation 2 where someone can represent the effectiveness as follows:
By making some short cuts, the RBE can be written as follows:
In this form the effectiveness has been represented in terms of effect cross-sections of tested radiation and the reference radiation and also the linear energy transfer of reference and the test radiations, rather than the absorbed doses or the radio-sensitivities parameter. The linear energy transfer is directly determined in irradiation experiments, but it is difficult to directly determine the effect cross-sections in irradiation experiments. Therefore, to represent the effectiveness directly by measurable physical quality parameters, the effect cross-section has rewritten in terms of other physical quality parameters. From the physical definition of the probability (Pt) of radiation effects, we have:
The factors σt and σr represent the geometrical cross-sections of targets in biological entities being at risk for test radiation and reference radiation respectively.
By substituting the relations (8) in equation (7) we get the form:
For mammalian cells exposed to high-LET radiation, we assume the same number of targets will expose to reference radiation and test radiation. Therefore the effect cross-sections σt and σr will be correspondent to each other, so that we obtain:
This is a new general form of effectiveness; this form can be applied for any end-point and for any radiation to determine the effectiveness. Although the probability (P) equals to intrinsic efficiency (ε) of damage multiplied by the number of biological segments are at risk (n0), but his definition can be formulated mathematically as follows:
In the special case, the probability of radiation damage can be written for both reference radiation and test radiation as follows:
Where Pt and Pr represent the probability of radiation damage due to test radiation and reference radiation, while εt and εr are intrinsic efficiency of damage due to test radiation and reference radiation, n0t and n0r represent the number of biological segments are at risks due to test radiation and reference radiation respectively. By substituting relations (12) in equation (10) we get a little bit complicated forms of RBEs:
The intrinsic efficiency of test and reference radiations can be written in terms of mean free path (λ) for linear primary ionization respectively as follows:
These equations are obtained in previous modeling work on experimental data related to cell inactivation and chromosomal aberration.
By substituting equality (15) and (16) in equation (14) the RBE can be written as follow:
For simplification, if we put m = 1 than the equation (17) will take the form:
Results and Discussion
The equation (18) gives novel mathematical form of RBE which can be used in determining the relative effectiveness of all types of high-LET radiations at lower doses. According to this form, the effectiveness of high-LET radiation can be divided into three cases; these cases are defined as follows:
Case number one: For
Case number two: For
Case number three: For
Since DNA is considered as the main target of radiation effectiveness then λ0 ≅ 2 nm, this value represents the spacing of the DNA double strands.
In first case; i.e. if λt = λ0 and λr = λ0, the damage occurred by ionizing radiation is optimized, and then the RBE will take the form:
In second case; i.e. if λt > λ0 and λr > λ0, the RBE will take the form:
And In the last case i.e. if λt < λ0 and λr < λ0, then the occurred radiation damage in this case is saturated and the effectiveness (RBE) will take the final form as follows:
Conclusion
The effectiveness of high-LET radiations has been represented in terms of two alternative physical quality parameters. These parameters are linear energy transfer (LET) and mean free path (λ) for linear primary ionizations. The new mathematical forms of relative biological effectiveness in previous three cases enable to quantify the effectiveness of high-LET radiation alternatively of radio-sensitivity parameters at lower doses region, and more effectively than just utilizing the absorbed dose.
The amount of absorbed energy into biological entities is not proper measure to quantify and interpret the effectiveness of high-LET radiations mechanism particularly at lower doses region. Spacing of energy deposited events in high-Let tracks and its relevant parameters such as mean free path and linear energy transfer represent very significant decisive factors which should be taken into account while explaining the effectiveness of high-LET radiations at lower doses region.
This approach will definitely assist in complementing the determination of the absolute effectiveness of high-LET radiations at lower doses regions for radiation protection.
Acknowledgment
We acknowledge the physics department for technical support and Sebha University for financial support to make this research published.
References
-
Turner JE, Bolch WE, Yoshida H, Jacobson KB, Wright HA, et al. (1991) Radiation damage to a biomolecule: new physical model successfully traces molecular events. Int J Rad Appl Instrum A 42: 995-1001.
-
Bond (1983) The Effects Of High Vs. Low-Level Radiation Exposure. Brookhaven National Laboratory, Upton, Ny 11973, 7-8.
-
Wambersie A, Menzel HG (1993) RBE in fast neutron therapy and in boron neutron capture therapy. A useful concept or a misuse? Strahlenther Onkol 169: 57-64.
-
Watt DE, Alkharam AS, Child MB, Salikin MS (1994) Dose as damage specifier in radio biology for radiation protection. Radiation Research 137: 410-413.
-
Kadri LA, Watt DE (1990) Physical quantification of the biological effectiveness of ionizing radiations. International journal of quantum chemistry 3053: 501-520.
-
Simmons JA (2001) Radiation risk from inhaled alpha emitters. Radiation Physics and Chemistry 61: 629-630.
-
Dietze G, Menzel HG (2004) Dose quantities in radiation protection and their limitations. Radiat Prot Dosimetry 112: 457-463.
-
Katz R (1994) Dose. Radiat Res 137: 410-413.
-
Chadwick KH, Leenhouts HP (2009) The RBE of low-LET radiations. J Radiol Prot 29: 445-447.
-
Harder, Blohm, Kessler (1988) Restricted LET remains a good parameter of radiation quality. radiation protection Dosimetry 23: 79-82.
-
Kiefer (1990) Biological Radiation Effects. Springer-Verlag Berlin Heidelberg, Germany.
-
Jäkel O (2008) The relative biological effectiveness of proton and ion beams. Z Med Phys 18: 276-285.
-
Belli, Cera F, Cherubini R, Dalla Vecchia M, Haque AM, et al. (1998) RBE-LET relationship for cell inactivation and mutation induced by low energy protons in V79 cells: Further results at the LNL facility. Int J Radia. Biol 74: 501-509.
-
Folkard M, Prise KM, Vojnovic B, Davies S, Roper MJ, et al. (1989) The irradiation of V79 mammalian cells by protons with energies below 2 MeV. Part I: Experimental arrangement and measurements of cell survival. Int J Radiat Biol 56: 221-237.