Journal of Hypertension and Management
Analysis of the Phenomenon of Endoleak of Type I A. Influence of the Mechanical Characterization of the Aorta
Mbodj C, Altnji H E*, Bou-Said B and Walter-Le Berre H
Laboratoire de Mécanique des Contacts et des Structures, INSA de Lyon, France
*Corresponding author:
Hussam Eddin Altnji, Laboratoire de Mécanique des Contacts et des Structures, INSA de Lyon, 18-20 rue des Sciences, 69621 Villeurbanne, France, Tel: 33-4-72-43-84-52, Fax: 33-4-78-89-09 80,
E-mail: hussam-eddin.altnji@insa-lyon.fr
J Hypertens Manag, JHM-2-014, (Volume 2, Issue 1), Research Article; ISSN: 2474-3690
Received: April 21, 2016 | Accepted: June 06, 2016 | Published: June 08, 2016
Citation: Mbodj C, Altnji HE, Bou-Said B, Walter-Le BH (2016) Analysis of the Phenomenon of Endoleak of Type I A. Influence of the Mechanical Characterization of the Aorta. J Hypertens Manag 2:014. 10.23937/2474-3690/1510014
Copyright: © 2016 Mbodj C, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
Models of the mechanical behaviour of arterial walls are required for mechanical applications in cardiovascular disease treatments, such as Endovascular Aneurysm Repair (EVAR) in particular, to contribute to the ability to predict type IA endoleak. In this work, an explicit finite-element in-house code was used to evaluate the stresses generated by the blood flow in a whole system consisting of the endograft, plaque, and aneurysmal aorta. The developed numerical model was modified to take into account the effect of anisotropy using a method of homogenization. A comparison of simulation results on the occurrence of Type IA endoleak between the aorta composed of a single layer and a true aorta, involving all three layers, was performed. In considering the anisotropy effect, the results showed the existence of two Young's moduli in the radial and longitudinal directions for the media, which is the middle layer of the aorta. Additionally, the simulations showed a significant difference in displacement and stress distribution in the true aorta composed of three layers when compared to simulations of the simplified aorta made up of one layer.
Keywords
Aortic aneurysm, Endovascular graft, Type IA endoleaks, Fluid-structure interaction, Homogenization
Introduction
Aneurysm is an enlargement or dilatation of the degenerated aorta. The aorta is made up of three layers: the intima (consisting of an endothelium layer), the media (composed of smooth muscle cells with elastin and collagen fibers), and the adventitia (the external layer composed of connective tissues with elastin and collagen fibers). Elastin degradation is related to dilatation while a rupture of the wall is a result of collagen degradation [1,2]. As the process of destruction increases, dilatation occurs. This leads to flow disturbances, changes in wall tension and, finally, rupture.
Endovascular techniques are appealing because they are minimally invasive. However, endovascular repair involves several complications, such as migration and endoleak that suggest a continuing or increasing risk of rupture. Migration was defined as stent graft movement ≥ 10 mm. An endoleak is defined as the presence of blood flow outside the lumen of the endoluminal graft but within the aneurysm sac. Endoleaks indicate incomplete exclusion of the aneurysm. The most serious type of endoleak is type I, which results from an incomplete seal between the endograft and the wall of the blood vessel.
Previous studies have investigated the effect of pulsatile 3D hemodynamics on the endograft placement by performing dynamic and fluid–structure interaction simulations [3]. They also investigated the stent-graft migration and type II endoleaks [4]. However, the aorta was considered to be as homogeneous continuum and the blood was modeled with neglecting the blood particle effects.
Previous studies carried out in the LAMCOS laboratory [5,6] developed a computational fluid-structure interaction using explicit dynamic finite-element in-house code (PlastD) of the complete system, i.e., the aneurysm, the atherosclerotic plaque, and the endovascular graft. This study provided an evaluation of the stresses generated by the blood flow in a stented abdominal aortic aneurysm simulation to detect the phenomena of type IA endoleaks. This simulation allowed for the detection and evaluation of the biomechanical factors that can influence the occurrence of type IA endoleaks. However, this work did not consider the anisotropic behavior of the aorta, nor the effect of the layers of the artery on the mechanical behaviour. The present paper is a follow-up to the previous work of the previous authors [6]. The main goal of this work is to investigate the effects of the anisotropic behavior of the aorta. Thus, we propose a homogenization method to involve the anisotropy by modifying the developed PLAST2 finite element code. Furthermore, we performed several simulations with the homogenized aorta of three layers. The obtained results were then compared to those obtained by [7] which considered isotropic and homogeneous aorta of only one layer.
Modeling
Fluid-structure interaction
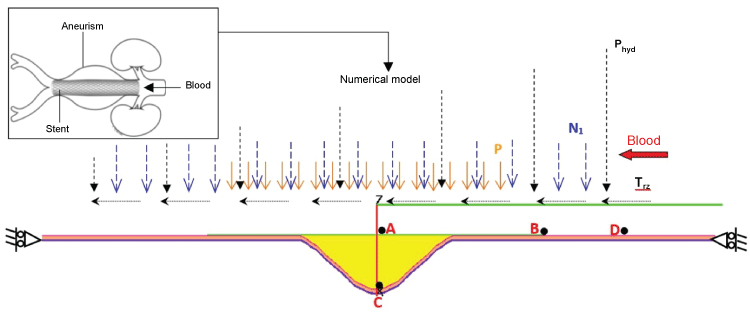
Different numerical methods were used for modeling the full stenting system, consisting of the stent, aorta, atheroma, and blood flow. The geometry of the whole system is shown in figure 1. The atherosclerotic plaque, the endoprosthes is wall, and the aorta wall are considered to be deformable. The aneurysmal aorta is of 60 mm diameter. The atherosclerotic plaque is situated just between the endograft and aneurysm wall.
The endoprosthesis and plaque are both considered to be elastic, isotropic homogeneous materials [5,8,9]. The rheological model used for the blood flow allows the representation of a large number of blood properties, and evaluate parietal constraints on the walls of the aorta and the stent. The Phan-Tien and Tanner model (MPTT) was used as a numerical model for the blood flow [7]. The viscosity of blood flow is that given by the Carreau equation. For modeling the axisymmetric stented aneurysm structure, we used the FE PLAST explicit dynamic finite-element in-house code developed at the LAMCOS laboratory and validated for many mechanical applications. The code is ideally suited for the contact between two deformable surfaces with viscoelastic behavior and fluid-structure interaction. The generalized Maxwell model was used to simulate the developed anisotropic, linear, and viscoelastic behavior of the artery wall. Finally, to simulate the stented aneurysm, a coupled fluid-structure finite element model was undertaken.
In this study and by using a homogenization method, we introduce the true anisotropic properties of the aorta. We aim to investigate the phenomena of endoleak at the proximal site of the aneurysm (Type IA). The effects of the heterogeneity (anisotropy) were integrated in the developed numerical model to take into account the effects of the different layers of the aorta on the mechanical behavior.
The elastic properties of the different aorta layers were taken from [10] (Table 1).
![]()
Table 1: Elastic properties [7].
View Table 1
Time dependent arterial pressure and radial pressure were applied on the endograft device and the inner surface of the aorta wall. Then, shear and normal stresses resulted by blood flow were applied on the whole system [5,6]. Both sides of the aorta surface were constrained in the axial direction, while the radial displacement was allowed. Further details about the explicit dynamic finite-element code and the contact algorithm between the deformable bodies are provided in [5].
The homogenization process determines the mechanical properties of a homogeneous material equivalent to the heterogeneous material. It can be considered as a particular method which eliminates microscopic quantities for the benefit of the macroscopic properties. Several numerical methods are proposed in the literature to homogenize a composite material. All these techniques require a Representative Elementary Volume (VER); the volume on which we apply the homogenization.
The microscopic study of the arterial walls shows a stratified and complex structure. Therefore, they can be compared to fibre-reinforced composite materials. Their mechanical properties are dependent on the fiber orientation of the fibers. In this work, the energy approach was used for the homogenization of the aorta wall.
Homogenization method
The energy approach is based on the principle of Hill's lemma which states that the average strain energy of a sample of volume V with the applied boundary conditions (uniform deformations or stresses at the boundary) is equal to the average strain energy of the macroscopic volume.
To apply this approach, a mechanical problem with conditions of homogeneous stresses (static approach) or homogeneous deformations (kinematic approach) was imposed on the edge of the VER.
Let V be the VER and the boundary that delimit the volume is ∂V.
The general approach is to determine the field of stresses and deformations in VER. Thus, the average values of stresses and deformations are obtained depending on the direction of the test in the volumetric element:
with (i = 1,..., 6 in 3D), (i = 1, 2, 3 in 2D)
If a mechanical problem is described with a kinematic approach, the macroscopic and microscopic deformation energies are given consequently by:
where is the global stiffness matrix, the applied deformation at the boundary
with The location operator stresses
Satisfying Hill's lemma theory:
With : the system with applied uniform deformations as a boundary condition. From this equality, we can deduce the overall stiffness of the homogenized material matrix
The orientation of collagen fibers was identified using the same technique of Holzapfel and al V [11]. In this study, an automatic technique was developed to allow identifying the favorite orientation of the collagen fibers observed by microscopy in the layers of the aorta. The tests are made from samples of human aortas. The angles values were 10° in media and 40° in the adventitia.
To homogenize the layers of the arterial wall, we used the data from literature, for the mechanical characterization of the different constituents, i.e., Young's modulus [12], Poisson's ratio and density [5,6], of the elastin fibers, collagen fibers, and smooth muscle cells. The homogenization procedure has been applied only to the media layer as it determines largely the elastic properties of the vessel.
The geometrical data was taken from literature [13], the diameter of a fiber was considered to be 100 (μm) and the values of volume fraction (α) were ranged from 0.3 to 0.4 (Table 2).
![]()
Table 2: Summary of mechanical characteristics of aorta constituents [12].
View Table 2
Numerical investigation of
We used finite element code ABAQUS to perform the numerical simulation using 2D element formulation. To study the media layer, we consider two similar plates with the same section and two different materials; one is composed of elastin fibers and the other of smooth muscle cells and collagen fibers. We supposed a condition of adhesion between the two plates since the friction conditions are not known between them. All the materials were considered as elastic isotropic material. The problem was described with a kinematic approach. We performed numerical tests, i.e. a tensile test in the directions 1 & 2 and a shear test. We imposed a deformation of ε = 0.05 at the boundary of the plate. The numerical simulation of each mechanical test allows us to calculate the state of stress.
Using the stresses values obtained at each point in the volume, we calculate the operator of location stresses . Then we use the average deformations and stresses of each test to calculate the stiffness matrix and the overall stiffness of the homogenized material matrix ,
The obtained values are:
The results showed the need of two Young's moduli in the radial and longitudinal directions for the middle layer of the aorta, i.e., the material can be considered as an isotropic transverse material. Thus by identification with the stiffness matrix of isotropic transverse material, we can deduce the mechanical properties:
Secondary Poisson's ratio
The numerical method was validated by performing a parametric numerical study of an elementary volume using the mechanical properties obtained with the homogenization. The same mechanical test and boundary conditions were applied. The stiffness matrix was deduced using the obtained values of stresses and deformations. We obtained them by identification of the elastic modulus and Poisson's ratio. These values were almost the same as those obtained by the homogenization which can confirm the validity of our method.
We also investigated the effect of changing VER, the imposed deformation and density of collagen fibers on the elastic models (E1, E2) and Poisson's ratio values (results not presented here).
The results showed that the surfaces values of VER between 9-25 mm2 give more stable results with respect to those smaller than 4 mm2. There was no remarkable variation of results when changing the values of the applied deformation.
Based on these results, the developed finite element PLAST2 code for the structure was modified to integrate the stiffness matrix for the transverse isotropic material. Then, we modified the viscoelastic model to take into account the different modules of elasticity (E1, E2). Thus, the modified code can read the new properties of materials to integrate equilibrium and constitutive equations and calculate the viscoelastic properties of isotropic transverse material.
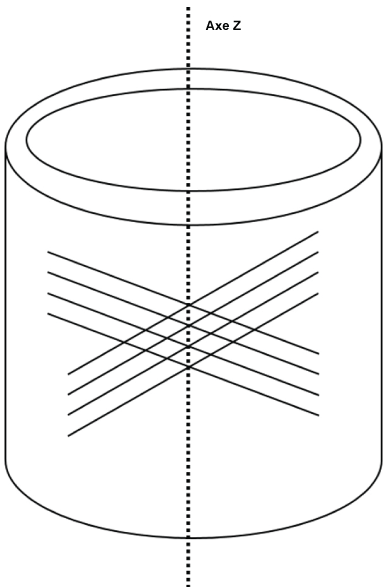
Considering an axisymmetric cylindrical geometry of the aorta with a cylindrical coordinate system (r, θ, z), with the privileged axis z, figure 2:

.
Figure 2: The State of stresses of the representative elementary volume (VER) for the media layer.
View Figure 2
The behaviour law of transverse isotropic material was deduced and can be given as follows:
With,
Et : Young's Modulus in the transverse direction (radial direction)
El : Young's Modulus in the longitudinal direction
Gtl : The shear model in the plan t, l.
: The secondary Poisson's ratios4In order to use the Generalized Maxwell model, we had to calculate the viscoelastic properties for every elastic coefficient, i.e. for Et, El, Gtl we will have (Gti,Tti), (), () respectively. We calculated the viscous deformation and deviatoric stresses variation for every direction.
Results
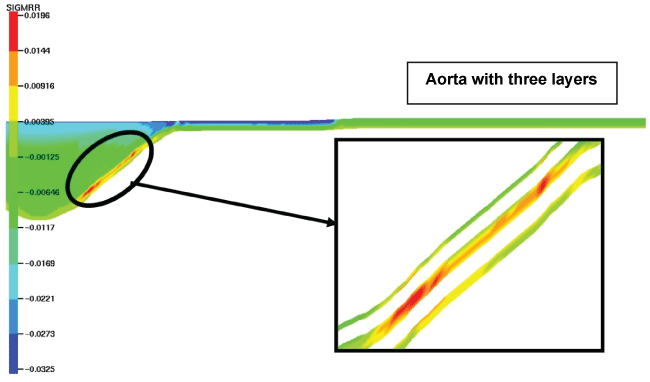
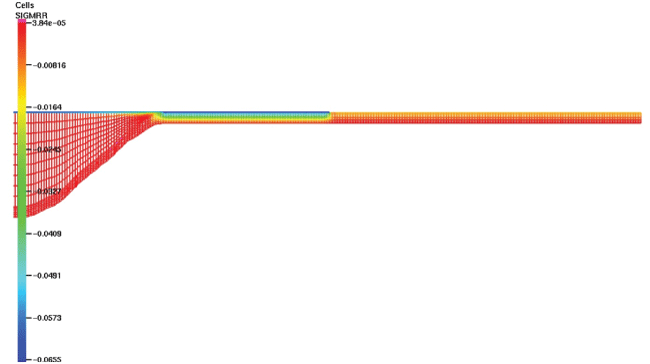
We evaluated the stresses distribution in the aorta composed of three layers (Figure 3). The results were then compared with those of only one layer. The radial stresses were symmetric with respect to the axis o-z. The maximal radial stresses (19500 Pa) were found in the aneurysmal sac; however, these values were highly different comparing with stresses values in the aorta composed only of one layer (11100 Pa). Also, the distribution of these stresses was different between the two cases. In the aorta with three layers, they were particularly concentrated in the media layer.
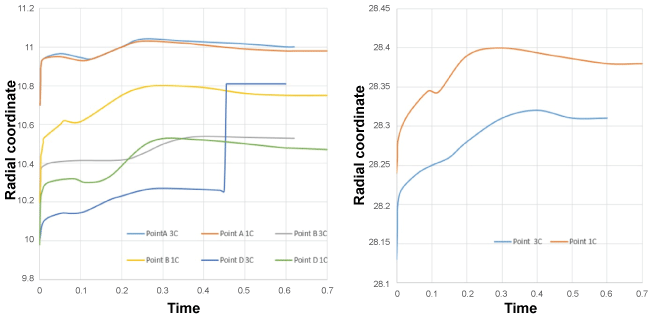
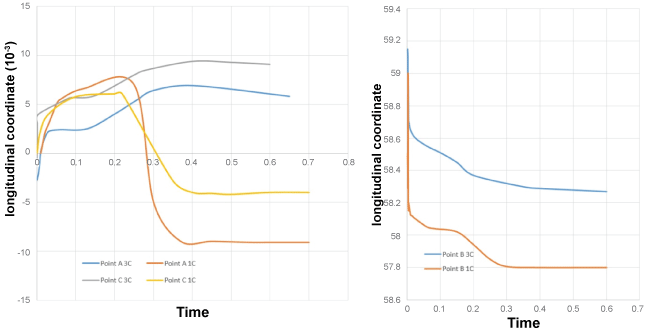
The evolution of displacement for 4 points (Figures 4, Figure 5 and Figure 6) was investigated and compared to the displacement results of the aorta with only one layer during the half of the cardiac cycle.
.
Figure 5: Point's positions in the aorta with one (1C) and three layers (3C)/radial coordinate.
View Figure 5
For the point A
Comparing these results with the results obtained by [5], these curves showed significant differences on the displacement evaluation during the half of the cardiac cycle when considering the three layers of the aorta. The maximal variation was found in the level of longitudinal displacement.
These results show the important influence of the three layers of the aorta on the displacement values during the half cardiac cycle.
.
Figure 6: Point's positions (A, B, C) in the aorta with one (1C) and three layers (3C)/longitudinal coordinate.
View Figure 6
.
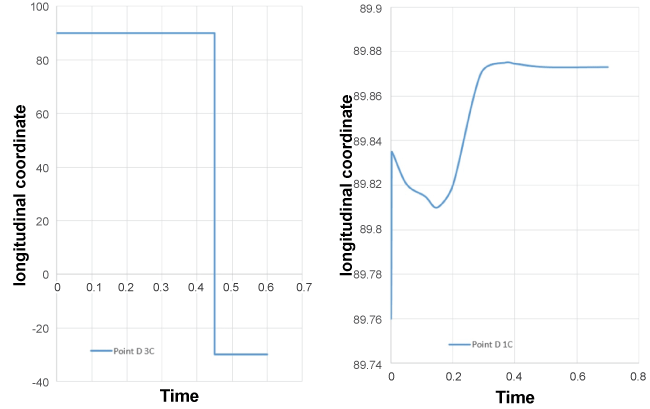
Figure 7: Point D position in the aorta with one (1C) and three layers (3C)/longitudinal coordinate.
View Figure 7
The results also demonstrated a significant difference in the contact evolution CE (endograft/aorta) between the two cases. When considering only one layer, CE can result in perfect adherence (endograft/aorta), however, CE can lead to separation (endograft/aorta) when the aorta wall was composed of three layers, figure7, figure 8 and figure 9.
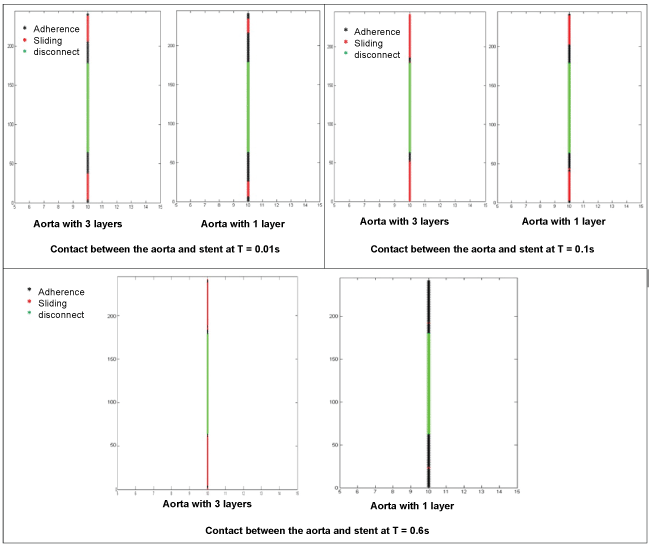
.
Figure 8: Contact (endograft/aorta with one and three layers) at t = 0.01s, 0.1s and 0.6s.
View Figure 8
The finite element code plast2 was modified to integrate the two Young's moduli obtained after homogenization. Figure 9 illustrate the stresses distribution at time 0.01s
The radial stress distribution was different with respect to the isotropic, homogeneous material. Considering the anisotropy, they were localized all through the external arterial wall and at the atheroma level.
The distributions of longitudinal, circumferential and shear stresses of 11 600 Pa, 76400 Pa, and 12600 Pa respectively showed that the maximum stresses were especially localized on the stent.
Discussion
This work presents numerical methods used for the modelling of the complete system endoprothese/aorta/atheroma/blood. The rheological model used for the blood flow can simulate the realistic properties of blood, and estimate the pre-stresses applied on the walls of aorta and endoprothese.
The developed explicit dynamic finite-element in-house code presents all its interest to control the contact between two deformable surfaces, to simulate the viscoelastic properties and the fluid-structure interaction.
Furthermore, in many numerical models, the aorta has been considered to be homogeneous isotropic, hyperplastic or viscoelastic. Nonetheless, most of the used numerical models are based on pseudoelastic approach, i.e. the material is considered to be hyperelastic in loading and elastic in unloading. The true aorta is non-homogeneous and shows anisotropic behavior [11,14-16]. Thus, it was necessary to develop a numerical model to include the effects of heterogeneity.
The used homogenization method, allowed modifying the numerical model endoprothese/aorta/atheroma/blood to integrate the effects of anisotropy.
We showed the differences between the model of the aorta composed of a single layer and a true aorta, involving all three layers. The evolution of the position of certain nodes is completely different according to the used model. There is also a significant difference at the level of the distribution of the maximal radial stresses, which are particularly located in media layer. The present work showed the importance of the microstructural study of the arterial walls by taking into accounts the heterogeneity and the effects of anisotropy
Conclusion
The major goal of this research was the implementation of a numerical model for modeling the microstructural behaviour of the vascular walls. We developed a computational fluid-structure interaction to investigate the effect of anisotropic properties of the aorta on the stress and displacement distributions, and consequently its incidence on type I endoleak. Thus, we realized a homogenization technique which can determine a mechanical characteristic of a homogenous material equivalent to a heterogeneous material. In this study, we used an approach which presents the homogenization as a numerical model of a mechanical test. This study was realized with finite element code ABAQUS. The results showed the existence of two Young's moduli in the radial and longitudinal directions for the middle layer of the aorta (the media). Based on these results, the developed numerical model was modified to consider the anisotropic behaviour of the aorta. The second main result of the work consists in the appraisal for the different behavior of the 3 layer model in comparison with the elastic isotropic model. The numerical simulation showed significant differences in results whether we take into account the three layers of the aorta, and consequently on the occurrence of type IA endoleak. Further work would focus on the development of a 3D homogenization numerical tool. This could evaluate the Young's modulus in the circumferential direction and also consider the viscoelastic behavior in order to determine the viscoelastic properties. Moreover, the aorta should be modeled with nonlinear anisotropic behavior. This work could rely on advanced medical imaging techniques to quantify the mechanical characteristics of blood vessels. The approximation of our axisymmetric model can be improved to respect reality especially by considering simulate stent crimping/inflation, 3D strut mechanics and wall blood interaction [17]. An experimental test application to the prosthetic case is also important, this can verify the validity of the models to replicate the same experimental data.
References
-
A Lumsden, Peter H Lin, Changyi Chen, Juan C Parodi (2007) Advanced Endovascular Therapy of Aortic Disease. Wiley Blackwell New Delhi India.
-
Gilbert R Upchurch, Enrique Criado (2009) Aortic Aneurysms. Humana Press New York, USA.
-
Li Z, Kleinstreuer C (2005) Blood flow and structure interactions in a stented abdominal aortic aneurysm model. Med Eng Phys 27: 369-382.
-
Li Z, Kleinstreuer C (2006) Analysis of biomechanical factors affecting stent-graft migration in an abdominal aortic aneurysm model. J Biomech 39: 2264-2273.
-
A A (2006) A contribution to the study of the behavior of abdominal aortic, Thesis-INSA-LYON, Lyon.
-
Anne Amblard, Helene Walter Le Berre, Benyebka Bou Said, Michel Brunet (2009) Analysis of type I Aendoleaks in a stented abdominal aortic aneurysm. Medical Engineering & Physics 31: 27-33.
-
A Amblard et B Bou-Said (2004) Modelling the blood flow in an aorta, chez Proceedings of the Leeds-Lyon symposium. United Kingdom.
-
F Auricchio, M Di Loreto, E Sacco (2001) Finite-element Analysis of a Stenotic Artery Revascularization through through a stent insertion. Computer Methods in Biomechanics and Biomedical Engineering 1-15.
-
Di Martino ES, Guadagni G, Fumero A, Ballerini G, Spirito R, et al. (2001) Fluid-structure interaction within realistic three-dimensional models of the aneurysmatic aorta as a guidance to assess the risk of rupture of the aneurysm. Med Eng Phys 23: 647-655.
-
Feng Gao, M Watanabe, T Matsuzawa (2005) Fluid-structure Interaction Within 3-layered Aortic Arch Model under Pulsatile Blood Flow. Sixth International Conference on Parallel and Distributed Computing Applications and Technologies (PDCAT'05) 989-992.
-
Gerhard A Holzapfel, Thomas C Gasser (2001) A viscoelastic model for fiber-reinforced composites at finite strains: Continuum basis, computational aspects and applications. Computer Methods in Applied Mechanics and Engineering 190: 4379-4403.
-
R Comolet (1984) Biomecanique circulatoire. Masson, New York.
-
Boerboom RA, Driessen NJ, Bouten CV, Huyghe JM, Baaijens FP (2003) Finite Element Model of Mechanically Induced Collagen Fiber Synthesis and Degradation in the Aortic Valve. Ann Biomed Eng 31: 1040-1053.
-
T Christian Gasser, Ray W Ogden, Gerhard A Holzapfel (2006) Hyperelastic modelling of arterial layers with distributed collagen fibre orientations. Journal of the Royal Society Interface 3: 15-35.
-
Sokolis DP, Boudoulas H, Karayannacos PE (2002) Assessment of the aortic stress-strain relation in uniaxial tension. J Biomech 35: 1213-1223.
-
Ohashi T, Abe H, Matsumoto T, Sato M (2004) Pipette aspiration technique for the measurement of nonlinear and anisotropic mechanical properties of blood vessel walls under biaxial stretch. J Biomech 38: 2248-2256.
-
David Perrin, Pierre Badel, Laurent Orgeas, Christian Geindreau, Aurelien Dumenil, et al. (2015) Patient-specific numerical simulation of stent-graft deployment: Validation on three clinical cases. Journal of Biomechanics 48: 1868-1875.