International Journal of Clinical Biostatistics and Biometrics
Target Frequency Analysis of functional MRI Data
Michael A. Frölich1*, Paul Jung2 and Shannon Starr2
1Professor, Department of Anesthesiology, University of Alabama at Birmingham, USA
2Associate Professor, Department of Mathematics, University of Alabama at Birmingham, USA
*Corresponding author:
Michael A. Frölich, Department of Anesthesiology, University of Alabama at Birmingham, 619 South 19th Street, Birmingham, AL 35249-6810, USA, Tel: (205) 975-0145, Fax: (205) 975-0145, E-mail: froelich@uab.edu
Int J Clin Biostat Biom, IJCBB-1-007, (Volume 1, Issue 1), Research Article; ISSN: 2469-5831
Received: September 11, 2015 | Accepted: October 31, 2015 | Published: November 02, 2015
Citation: Frölich MA, Jung P, Starr S (2015) Target Frequency Analysis of functional MRI Data. Int J Clin Biostat Biom 1:007. 10.23937/2469-5831/1510007
Copyright: © 2015 Frölich MA, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
Background: The field of functional magnetic resonance imaging (fMRI) has grown in usage, applications, and complexity. The results of a general linear model (GLM) analysis vary from one investigator to another as they depend on image preprocessing, model choices and physiological assumptions. There is a need for a simple, efficient and consistent analysis method.
Methods: We propose the target frequency analysis (TFA) as an intuitive, computationally efficient method to analyze data from block design fMRI experiments. We illustrate its utility with a traditional auditory experiment and develop the theoretical foundation on which the method is based.
Results: We show that the TFA correctly identifies activation of the primary and secondary auditory cortex in response to a periodic auditory stimulus. We demonstrate that the amplitude of a single frequency component or the sum of several frequency components of a white noise signal have a Nakagami probability distribution. The percentiles of this null distribution can be used to determine the activation threshold of an fMRI experiment.
Conclusions: The proposed TFA approach does not require assumptions of the GLM approach such as the a priori knowledge of the shape of the stimulus function or hemodynamic response function. The method is computationally efficient and has great potential as supplementary analysis of block design fMRI experiments.
Keywords
Fourier transform, Functional MRI, Frequency analysis
Summary statement
We provide the theoretical foundation of a frequency based fMRI analysis approach, which does not depend on many assumptions of existing GLM based approaches. We illustrate its application using an auditory fMRI example.
Introduction
Functional magnetic resonance imaging (fMRI) methods have expanded in scope and level of sophistication. Yet, the user dependent nature of fMRI analyses has led some to become skeptical of the validity of the data and scientific hypothesis generated. The prevailing statistical technique is the general linear model (GLM). It is used ubiquitously because it is very flexible, but it typically requires certain data manipulations and depends on specific physiological assumptions, which may not be met. For example, the response to a task has been shown to be stimulus specific [1] and the response changes with age or from person to person [2]. It has been documented that the fMRI response depends on the subject as well as the day and time of the scanning session [3]. It can easily be demonstrated that just minor modifications of the input onset values used in existing imaging analysis packages alter the results significantly (an example is given in figure 1). The subjective nature of imaging analyses makes the interpretation of functional imaging studies, particularly those that investigate complex cognitive tasks, problematic. In classical statistical applications, the investigator can use descriptive methods to provide an overall sense of the data. However, the complex nature of neuroimaging analysis makes it difficult to generate a simple statistic that provides an intuitive description of the experiment.
.
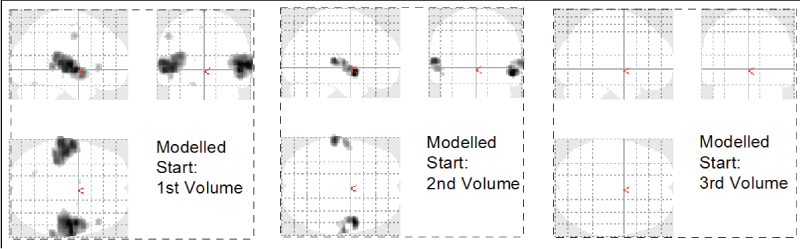
Figure 1: Phase dependence of GLM based image analysis. The auditory experiment was timed such that the stimulus onset was expected to coincide with the 2nd recorded brain volume. A modified analysis with onset at Volume 1 shows more activation, an onset at Volume 3 shows no activation at all.
View Figure 1
With the goal in mind to find a method for block design fMRI experiments that is unconstrained by many of the assumptions of the GLM method, we first contemplated a simple analysis of the temporal signal variance. The basic idea was that a brain MRI signal recorded over time from a person at a resting state (i.e. not subject to an experimental stimulus) would have temporal variability attributable only to the random noise of the MRI signal. By contrast, the signal time course of a person exposed to a repeated task would have a larger variability in areas of the brain that respond to the task, reflecting both the variance due to the task as well as the variance due to the random noise. Unfortunately, this simplistic approach fails to identify task related activity as it ignores other very important sources of variances such as the MRI signal drift and physiological noise (rhythmic signal changes due to heart beat and respiration). We realized that any useful method would have to somehow extract the signal due to the periodic task while ignoring any other signal variability (noise). This thought gave rise to the target frequency analysis (TFA) proposed in this paper. This approach builds on existing frequency based analysis concepts with a new focus on the amplitude of a single frequency. We also generalize the concept slightly to include the target frequency (TF) and its harmonics and prove the theoretical foundation of the proposed method rigorously. We then designed an fMRI experiment for the empirical comparison of the traditional GLM analysis and the new TFA approach. We chose an auditory task for this experiment since this type of stimulus has been well validated in BOLD fMRI experiments. Our hypothesis was that the TFA approach would produce qualitative comparable result when compared to the traditional GLM analysis.
Materials and Methods
Subjects and recruitment
To demonstrate the concept of the TFA we conducted an auditory fMRI study in 12 human volunteers. Participants were recruited by public advertisement. During a screening visit we performed a focused history and physical examination and we obtained written informed consent. Handedness was assessed using the Edinburgh Handedness Inventory [4]. We included healthy right-handed volunteers ages 21 - 40. Exclusion criteria were any significant preexisting pulmonary or cardiac disease, a body mass index > 40 kg/m2, a history of substance abuse and a current prescription of any neurotropic medication. On a separate day, participants underwent an fMRI session consisting of an orientation scan, a structural MRI scan and a 5-minute echo planar imaging (EPI) session on a Siemens Allegra 3T scanner.
Technical information and GLM analysis
We acquired 150 functional images at a near isovolumetric voxel resolution of 4 mm and a repetition time of 2000 ms. Functional MRI data were stored in Siemens DICOM format and then converted to 4D-single Nifti files and realigned in Matlab R 2012b (Mathworks, Natick, MA) using tools built into statistical parametric mapping (SPM 12, London, UK). These were the only preprocessing steps needed for the TFA. The GLM analysis required a few extra steps: after realignment, images were co-registered to the structural scan, spatially normalized and smoothed with the default 8 by 8 by 8 mm smoothing kernel. To define the expected fMRI activation time course, we used the default parameters in SPM where the fMRI BOLD response is modeled as a convolution of a box-car function per experiment design and a 2-component gamma mixture model for the hemodynamic response function (canonical hrf). To select the most parsimonious model, no motion regressors, temporal or dispersion derivatives were added.
During the functional scans, volunteers listened to eight second blocks of music (created from royalty free audio clips of varying music genres), starting at the 8th second and alternating with 8-seconds of silence. Music stimulus and scanner start were synchronized by count down. We used the fMRI compatible headset provided from the manufacturer (Siemens) both to shield subjects from scanner noise as well as to play the auditory stimulus (music segments). The first two brain volumes, taking up the first 4 seconds after scanner start, were not recorded as they constitute equilibration ("dummy") scans. We performed two analyses: a traditional GLM analysis using the statistical parametric mapping (Welcome Trust Centre for Neuroimaging, London) and a TFA analysis. A family-wise error correction threshold of p = 0.05 was used for the results report. Average activation was calculated as the mean of the SPMs for each participant. The resulting t-maps were then rendered to an inflated brain surface using the BrainNet Viewer [5].
Target frequency analysis (TFA)
We define the TF as the particular frequency that corresponds to the experimental task. In the auditory example, we play 8 - second sequences of music that alternate with 8 - second sequences of silence. This gives a task period of 16 seconds or, in terms of frequency, a task frequency of 1/16 Hz. In the analysis, we target the same frequency component, the 1/16 Hz frequency component and call this our TF. Realigned images were loaded as 4-dimensional matrix into Matlab 2014a (Mathworks, Natick, MA). After removing low signal intensities, which represent voxels outside the brain, images were mean-centered and scaled by subtracting the temporal mean signal and dividing by the temporal signal standard deviation for all brain voxels, using matrix commands in Matlab. This was followed by extracting the TF - the one signal frequency with a period of 8 seconds that corresponds to the period of the auditory experiment - using the Goertzel algorithm in Matlab [6]. Images were then co-registered manually to match in anterior commissure (origin), size and spatial rotation with the t-maps generated via the GLM analysis to allow for the illustration of both methods in figure 2. As statistical threshold, we used the 95% percentile of the Nakagami (m = 1, = 150) distribution [the rationale for this will be explained below]. Average activation was calculated as mean amplitude values across participants.
.
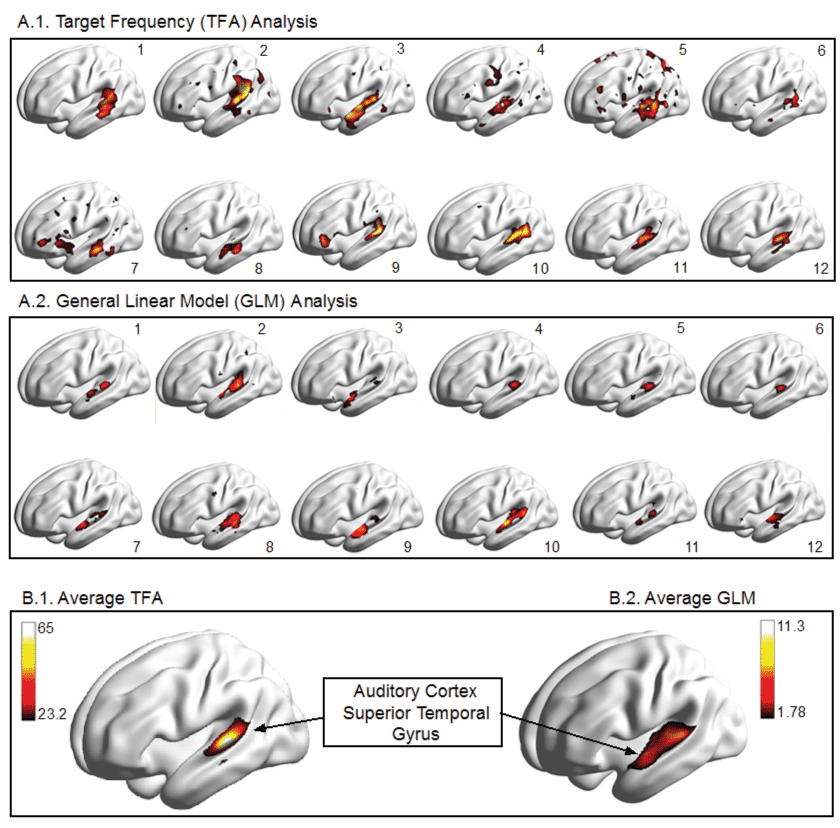
Figure 2: Illustration of Results for Auditory fMRI experiment in 12 human volunteers, analyzed in the time domain using a mass-univariate t-test with an FWE corrected threshold at a p = 0.05 level versus a TF based analysis using only one (the first) harmonic and a threshold determined by the 95th percentile of amplitude distribution under the null hypothesis of a white noise signal (Nakagami [1,150]).
View Figure 2
To establish a threshold for declaring voxels active, we investigated the behavior of a random noise BOLD signal, i.e. a signal that one could expect if no stimulation was presented to a subject. First, we used simulation methods to generate independent Gaussian distributed noise. After a Fourier transform of this random signal, we studied the characteristics of all frequency components as well as individual frequencies using three-dimensional histograms and the distribution fitting tool in Matlab (figure 3). Based on empirical observations, we postulated that the amplitude of a single frequency of a white noise signal has a Nakagami distribution. We then applied standard mathematical methods to provide a proof to support our observation.
.
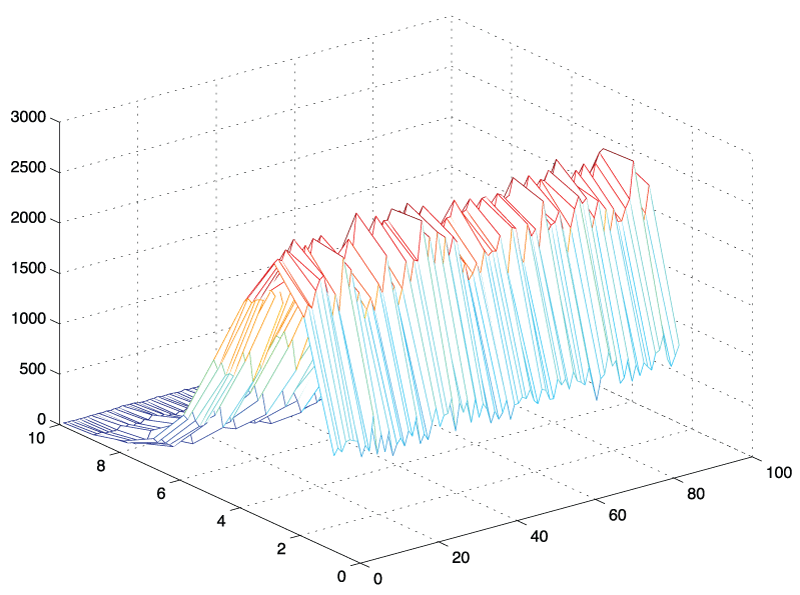
Figure 3: 3D - histogram of amplitude values: N = 10,000 standard normal random vectors of length, L = 180 were generated, transformed into frequency space using the fast Fourier transform in Matlab and plotted as 3D - histogram from bin k = 1 to 89. It can be seen that the shape of the histograms are similar regardless of frequency bin.
View Figure 3
Results
Results from an auditory experiment
The results of our auditory study are illustrated in figure 2. The left auditory cortex, located within the lateral fissure and the superior aspect of the temporal gyrus, is shown to be active in each of twelve participants. It can also be seen that there is considerable variability from one person to another. However, the location of activation within the superior temporal gyrus appears to be relatively consistent across analysis methods (GLM vs. TFA). In addition to cortical renderings for each participant we show the average activation. The threshold of the amplitude variable is based on the null distribution, which we have derived as Nakagami (m = 1, = 150). The 95th percentile of this distribution equals 23.22. When this threshold is applied to the auditory experiment we know that 5% of the voxels displayed may be included simply by chance.
One of the advantages of the TFA is that the method is independent of the phase shift of the signal or delayed onset time of the perceived stimulus. In a GLM based analysis the same variations would drastically alter the results as we demonstrate in figure 1, which shows the results of a GLM based analysis with varying onset times. The onset of auditory activation was timed to occur at the end of the second volume. Given the stimulus start at 8 seconds, the first 2 volumes discarded as equilibration scans, a TR of 2 seconds, and a period of 8 volumes (4 music on / 4 music off), a proper onset was expected to coincide with the second brain volume. However, a modified analysis with onset at the first brain volume shows significantly larger activation clusters.
Investigation of the frequency amplitude distribution
BOLD signals are discrete time series, which can be transformed into frequency components using the Fourier transform. This transformation maps N signal values in the time-domain to a single complex number (Zk), which represents a single frequency component of the time signal. The transformation depends on the value of the index k, which ranges from 0 to N - 1. The Fourier transform can therefore generate N complex numbers. The inverse Fourier transform uses N complex numbers to generate one real number in the time domain. The single complex number resulting from a (forward) Fourier transform gives rise to the amplitude and phase of a frequency component. We want to examine the distribution of the amplitude representing a single frequency component as well as the distribution of the sum of amplitudes representing the TF and its harmonics.
An initial approach was based on simple simulation experiments in which we generated a white (standard Gaussian) noise signal and evaluated its frequency components. We generated 1,000 time signals of arbitrary length t = 180 and extracted individual frequency components from this sample using a Matlab simulation. The histograms for the individual frequency components starting from k = 2 to k = N/2 - 1 are illustrated in figure 3. It became apparent that the shape of the histograms and the amplitude values for these frequency components appeared to be identically distributed. Comparing for example an arbitrary 7th and the 42nd frequency component, we found that their amplitude values had the same distribution, an observation that was not intuitively obvious. An empirical investigation using Matlab's distribution fitting tool further suggested that the shape of these histograms appeared to have the contour of a Nakagami distribution. In the following section, we state this observation as a theorem, followed by the outline of a mathematical proof. The rigorous proof of the amplitude distribution theorem is given in the appendix.
Amplitude distribution theorem
Suppose that x1,...,xN are IID standard Normal random variables. For any , let us define:
Where Zk represents the Fourier transform of a single frequency bin k, Xk represents the real part, Yk the imaginary part, Ak the amplitude of a single frequency and A+ the amplitude of a sum of frequencies. Assume that the conditions R < (N/2) and the set S = {k1,...,KR} are all distinct values satisfying 0 < kr < N/2 for r = 1,...,R are met. We then have that Ak is a Nakagami random variable with parameters m = 1 and = N and that A+ is a Nakagami random variable with parameters m = R and = NR. Summarizing, we have:
Outline of a proof
We first establish that the real and imaginary part of a random noise signal are independent and that they are distributed N (0, N/2) except for the two special cases where k = 0 or k = N/2. Based on these results we establish the distribution of the amplitude of a frequency component by squaring and adding the real (Xk) and imaginary parts (Yk) and taking their square root. We work with a joint distribution of two frequency components because this leads us to a result that is applicable for the simple case of one frequency component as well as the case when we consider the sum of several harmonics. A detailed proof is provided as appendix.
Discussion
The result of a general linear model (GLM) analysis varies from one investigator to another as it dependents on image preprocessing, model choices and physiological assumptions. A brief review of the GLM approach will illustrate this point. This followed by a discussion of the motivating ideas behind the TFA approach.
Basic idea of the TFA of fMRI data
The idea of the TFA is that the agreement of the BOLD signal (in response to a periodic task) and a sine wave with matching frequency is a measure of brain activity; a measure of this agreement is the amplitude of the TF. This concept may be best illustrated using a concrete example: Consider an experiment whereby a person's right hand is immersed into a container filled with ice for 8 seconds followed by immersion into tepid water for 8 seconds and this alternating stimulus is continued for 5 minutes. We now have a stimulus period of 16 seconds and a stimulus frequency of 1/16 Hertz (Hz). When observing the BOLD signal time-course, we expect peaks and troughs of the signal with the same frequency, our TF. As we have demonstrated in a psychophysical experiment [7] a temporal shift of this curve occurs if it takes a while as the brain registers the signal as increasingly unpleasant and there may be a similar lag in the recovery from each cold stimulus but, on average, the periodicity of the signal is preserved. After performing a Fourier transform of the observed BOLD signal we have that the amplitude of the TF is a measure of agreement of the observed signal with the task and hence a measure of brain activity.
One might argue that the shape of a sine wave may not be a good enough match to the observed signal and that the convolution of an assumed stimulus function and an assumed hemodynamic response function - as done in the traditional GLM analysis - might be a better match. Given the discrete nature of fMRI experiments (data are collected every time a whole brain image is obtained rather than continuously), the best possible match of the shape of the TF sine wave can be accommodated by adding the overtones (or harmonics) to the TF in the analysis. Because our sample rate - determined by the scan repetition time - is typically low in fMRI experiments, there are only few harmonics that we can consider. Given this limitation of a functional fMRI experiment, it is important to realize that all information from the discrete time-series about the shape of the sinusoid TF is contained in these harmonics.
In order to establish a statistical measure of the amplitude of the TF, we need to characterize its distribution. More precisely, if we wanted to develop a statistical threshold, we needed to establish the null distribution of the TF amplitude (the distribution of the TF amplitude when we only have a random noise signal). As we demonstrated in our mathematical treatment of this concept, the TF amplitude has a Nakagami distribution. We also prooved that the amplitude of each frequency component of a random noise signal, as well as the sum of several frequencies, are Nakagami distributed with the important exception of the "direct current" (DC) component and the Nyquist limit frequency. This proof establishes the theoretical basis by which we can calculate an amplitude threshold value which can be used to declare brain voxels as active.
There is one important distinction between the TFA and the GLM approach which affects the issue of multiple comparisons. The GLM approach is correctly described as a "mass-univariate" analysis, that is the BOLD signal time course is analyzed for each brain voxel separately. The result is a three-dimensional map of the t-statistic generated for each of thousands of brain voxels. There are several methods to deal with the ensuing multiple comparison issue. The most widely adopted method requires smoothing of the data and invokes the concept of Gaussian field theory [8]. By contrast an adjustment for multiple comparisons is not used in the TFA because the threshold for active voxels is simply based on the distribution of the TF amplitude, a single calculated value (outcome) rather than a statistic. One can understand this important difference better when realizing that, in the TFA, we extract a single value of interest, the amplitude of our TF that we are interested in. In the GLM analysis each brain voxel is represented by a time-series of N values that are being summarized using the t-statistic. Thus, in the TFA we are reframing the problem to evaluating a distribution of the amplitude of a single frequency (Ak) whereas in the GLM we are evaluating a three-dimensional matrix of t-statistics which requires considerations multiple comparisons.
Synopsis of the general linear model analysis of fMRI data
The GLM based analysis of fMRI data can be thought of as an extension of a simple bivariate regression where we examine the correlation of observed MRI intensity values and predicted MRI intensity values. There are several physiological assumptions when constructing the predicted MRI intensity values. The predicted signal is actually derived as a convolution of 2 functions, a stimulus function, g(t) and the hemodynamic response function (hrf), h(t) where t denotes time. In a block design, it is generally assumed that the stimulus function, g(t) is a "stick function" that takes on two values: one during the task and zero in the absence of the task. It is needless to say that this assumption is hardly realistic for cognitive experiences such as pain, because the intensity of pain typically builds up and gradually disappears after the stimulus is removed. Utilizing the classic example of the cold pressor test as experimental pain model, we showed that this assumption is not valid at all [7]. In fact, certain experimental tasks may even produce BOLD decreases rather than increases, a phenomenon that would completely negate the GLM model assumption [9]. The shape of the hrf, h(t) is determined by the hemodynamic coupling of a neurological impulse and the associated change in regional brain blood flow; that is, a neurological event in the brain triggers a change in regional cerebral perfusion to that brain area. Nikos Logothetis [10] is credited with characterizing the shape of the hrf in combined electrophysiological and MRI experiments in the primate brain. In analysis packages, the hrf is often modeled as a mixture of two gamma probability distribution functions [11]. Although the hrf appears to be consistent when evaluated within the context of visual experiments (and the vision cortex), there is considerable doubt that the shape of this function is consistent across a variety of brain regions [12]. This is another important assumption that is likely not met. Disregarding the potential violation of assumptions, we would construct the predicted BOLD response as convolution function, f (t) = (g * h) (t). Finally, the requirement for spatial smoothing as a prerequisite to calculate a suitable family-wise error threshold based on random field theory is another prerequisite that has been seen as counterintuitive to the pursuit of higher spatial resolution in fMRI imaging. It may be for these reasons that Poline et al. wondered whether the "love for the GLM would last forever" [13].
We revisited existing analysis approaches in search of a method that would neither require knowledge of the shape of the stimulus or hemodynamic response function. A frequency based analysis approach appeared to fit that profile. Bandettini and Hyde introduced this approach early in the development of fMRI analysis methods [14]. In their paper, Bandettini et al. investigated a signal both in time and frequency domain. They also paid attention to the first harmonic of the task frequency and determined that this frequency carries some information about the task. Two years later Sereno et al. published a result on a frequency-based approach to analyze vision data [15]. However, the frequency based methods used in retinotopic experiments where design to make use of phase-differences in the stimuli. When one intends to develop a more flexible approach the focus on frequency phase may not be desirable. In years to follow, most investigators focused on analyses in the time rather than frequency domain and, most recently, frequency based approaches were revisited by scientists interested in resting-state fMRI [16].
Our interest in a frequency-based approach was directed at finding an analysis tool that did not require many assumptions, yet allowed us to remove any confounding information in the signal, that is unwanted noise or signal drift. The analysis concept proposed in our paper is that, in a block design fMRI experiment, the amplitude of the TF (the frequency that correlates with the experimental stimulus) represents the agreement of MRI signal and experimental task, i.e. brain activity. We demonstrate that the frequency amplitude of a random signal, after Fourier transform, has a Nakagami probability distribution with the shape parameter m = 1 and dispersion parameter = N. The sum of the TF and its harmonics has a Nakagami (m = R, = NR) distribution where N is the signal length and R the number of harmonics included. The applied rationale of this work is to establish a null distribution of the amplitude of a single frequency or the sum of frequencies, as a frame of reference to which we can compare the alternate distribution of an observed signal obtained while a periodic task is applied. The null distribution (white noise) can be viewed as a distribution of a random variable that informs us about the probability of observing extreme amplitude values in a brain voxel simply by chance.
The Nakagami distribution is ubiquitous in applications in the technical sciences. This distribution was originally proposed at a symposium on radio wave propagations refined models for the pdf of signal amplitude exposed to fading of a wireless communication signal [17]. In medical imaging the distribution has been proposed to characterize ultrasound tissue because the envelope of the ultrasound radiofrequency (RF) signal can be described by this distribution and the parameters can be used to distinguish tissue types [18]. A new application of the Nakagami distribution, in functional magnetic resonance imaging (fMRI) research, is described here. In an fMRI block design, a person receives a certain stimulus in a periodic fashion. The repeated application is intended to overcome the problem of a relatively low signal-to-noise ratio. During the stimulus application, repeated brain images are obtained. The agreement of the time-course of the fMRI signal and the period of the stimulus application can be used to detect regions in the brain that respond to the experimental task. The Nakagami distribution is related to the Gamma and distribution, which are more commonly used in statistics. In particular, the Nakagami distribution can be generated from a - distribution with degrees of freedom equal to two times the shape parameter, followed by a scaling transformation. In particular, if , then
In the auditory example, included as proof of concept, we have extracted the frequency component of the signal that corresponds to the auditory task. We contrast the results of a simple GLM analysis with those of the newly introduced TFA. It can be seen that activation of the auditory cortex is observed with either method (see figure 2), thus providing the qualitative evidence in support of our hypothesis. In addition, the TFA method we propose provides results with a very fast computational sequence. Results are unaffected by phase shifts of the stimulus and variations in stimulus or hemodynamic response function. We introduce the theoretical distribution of the frequency amplitude as a means to generate a statistical threshold defining the probability of false positive results.
In summary, we propose the TFA method as alternative tool to analyze fMRI data because the method is computationally efficient and is not affected by misspecifications of anticipated BOLD response in terms of onset, shape or variability across different regions of the brain. As such the method should have great utility as screening tool or as supplementary analysis of block design fMRI experiments.
IRB
UAB protocol numbers F081016014 and X081016014. Most recent approval period: 8-27-14 to 8-27-2015. Signed by Maureen Doss.
References
-
Bornhovd K, Quante M, Glauche V, Bromm B, Weiller C, et al. (2002) Painful stimuli evoke different stimulus-response functions in the amygdala, prefrontal, insula and somatosensory cortex: a single-trial fMRI study. Brain 125: 1326-1336.
-
Jacobs J, Hawco C, Kobayashi E, Boor R, LeVan P, et al. (2008) Variability of the hemodynamic response as a function of age and frequency of epileptic discharge in children with epilepsy. Neuroimage 40: 601-614.
-
Aguirre GK, Zarahn E, D'esposito M (1998) The variability of human, BOLD hemodynamic responses. Neuroimage 8: 360-369.
-
Oldfield RC (1971) The assessment and analysis of handedness: the Edinburgh inventory. Neuropsychologia 9: 97-113.
-
Xia M, Wang J, He Y (2013) BrainNet Viewer: a network visualization tool for human brain connectomics. PLoS One 8: e68910.
-
Goertzel G (1958) An Algorithm for the Evaluation of Finite Trigonometric Series. Am Math Mon 65: 34-35.
-
Frölich MA, Bolding MS, Cutter GR, Ness TJ, Zhang K (2010) Temporal characteristics of cold pain perception. Neurosci Lett 480: 12-15.
-
Worsley KJ, Friston KJ (1995) Analysis of fMRI time-series revisited--again. Neuroimage 2: 173-181.
-
Shmuel A, Augath M, Oeltermann A, Logothetis NK (2006) Negative functional MRI response correlates with decreases in neuronal activity in monkey visual area V1. Nat Neurosci 9: 569-577.
-
Logothetis NK (2003) The underpinnings of the BOLD functional magnetic resonance imaging signal. J Neurosci 23: 3963-3971.
-
Friston KJ, Fletcher P, Josephs O, Holmes A, Rugg MD, et al. (1998) Event-related fMRI: characterizing differential responses. Neuroimage 7: 30-40.
-
Ances BM, Leontiev O, Perthen JE, Liang C, Lansing AE, et al. (2008) Regional differences in the coupling of cerebral blood flow and oxygen metabolism changes in response to activation: implications for BOLD-fMRI. Neuroimage 39: 1510-1521.
-
Poline JB, Brett M (2012) The general linear model and fMRI: does love last forever? Neuroimage 62: 871-880.
-
Bandettini PA, Wong EC, Hinks RS, Tikofsky RS, Hyde JS (1992) Time course EPI of human brain function during task activation. Magn Reson Med 25: 390-397.
-
Sereno MI, Dale AM, Reppas JB, Kwong KK, Belliveau JW, et al. (1995) Borders of multiple visual areas in humans revealed by functional magnetic resonance imaging. Science 268: 889-893.
-
van den Heuvel MP, Hulshoff Pol HE (2010) Exploring the brain network: a review on resting-state fMRI functional connectivity. Eur Neuropsychopharmacol 20: 519-534.
-
Hoffman WC (1958) Statistical Methods in Radio Wave Propagation: Proceedings of a Symposium Held at the University of California, Los Angeles.
-
Caixinha M, Jesus DA, Velte E, Santos MJ, Santos JB (2014) Using ultrasound backscattering signals and Nakagami statistical distribution to assess regional cataract hardness. IEEE Trans Biomed Eng 61: 2921-2929.